import math
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist
def f(x):
# 自定义函数
# 因为有形参x,故不用sympy声明符号变量
return 5*pow(x, 2) + 3*x + 4
def goldOpt(a, b, theta):
# 黄金分割法求单峰函数极小值
alpha = (math.sqrt(5) - 1) / 2
t1 = a + (1 - alpha)*(b - a)
t2 = a + alpha*(b - a)
step_num = 0
while abs(b-a) > theta:
step_num += 1
f1 = f(t1)
f2 = f(t2)
if f1 < f2:
b = t2
t2 = t1
f2 = f1
t1 = a + (1 - alpha)*(b - a)
else:
a = t1
t1 = t2
f1 = f2
t2 = a + alpha * (b - a)
x_opt = (a + b) / 2
y_opt = f(x_opt)
print((x_opt, y_opt))
return (x_opt, y_opt, step_num)
x_opt, y_opt, step_num = goldOpt(a=-2, b=2, theta=0.03)
X = np.lin









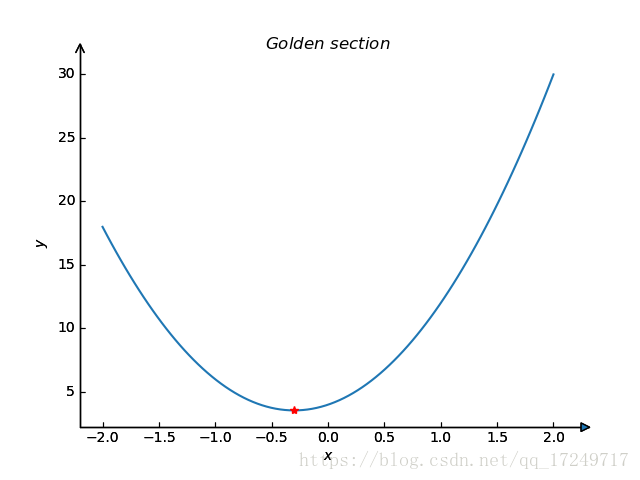
 本文详细介绍了如何使用Python编程实现黄金分割法,这是一种经典的数值优化方法,用于寻找非线性规划问题的极小值点。通过实例展示了算法的步骤和代码实现,帮助读者理解并应用该方法解决实际问题。
本文详细介绍了如何使用Python编程实现黄金分割法,这是一种经典的数值优化方法,用于寻找非线性规划问题的极小值点。通过实例展示了算法的步骤和代码实现,帮助读者理解并应用该方法解决实际问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2562
2562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








