实验四 噪声时的 Kalman滤波器算法在实例程序设计

实验4.1Matlab程序代码 1、模拟一个状态空间模型， - T=0.2， Q=0.9，R=0.6是模型的参数 - sigma=sqrt(Q)计算噪声方差的标准差 - I=eye(4)返回一个4*4的单位矩阵 - N=200是时序数据的长度 - a=0.11是阻尼系数 - w和v分别是两个高斯白噪声信号，服从均值为0、方差为1的正态分布 - Phi、G和H分别是系统动态方程、控制向量和观测矩阵的系数矩阵 - xr(:,1)表示初始的、真实的状态量（4维），其中xr(4,1)=w(1,1)表示第四个状态为初始的噪声值。   图1 模拟一个状态空间模型 2、计算给定状态方程和观测矩阵的卡尔曼滤波器的估计值。 具体来说，循环迭代状态向量（xr）和观测向量（z），使用先前估计的状态向量和观测到的数据点计算下一步的状态向量。同时，该代码还初始化了估计向量、误差协方差矩阵等变量。 - xr(:,i)表示状态估计 - z(:,i)表示观测值 - xe(:,1)是初始状态估计向量，全为0； - Ppos是误差协方差的估计的先验（状态预测时，误差协方差估计的对角线）； - Ppre(:,1)和Pest(:,1)是误差协方差的先验和后验，也就是在每个时间步之前和之后分别估计的协方差矩阵对角线。   图2计算给定状态方程和观测矩阵的卡尔曼滤波器的估计值 3计算给定状态方程和观测矩阵的状态估计值。具体来说，在每个时间步中，先利用当前时刻的协方差矩阵进行状态预测，并使用观测到的信息来更新误差协方差矩阵和状态估计向量。同时，还计算了最优增益矩阵K。 - x(:,i)表示状态预测值 - Pneg是误差协方差的估计的先验（状态预测时）； - K(:,i)表示的是最优增益矩阵，用于将状态预测与观测值相结合以计算后验状态估计； - Ppos是误差协方差的后验（状态估计时）； - Pest(:,i)是Ppos的对角线上的元素，表示各维度状态估计误差估计； 在每个时间步中，先进行状态预测，计算下一步x，并利用先前的协方差矩阵计算提前估计的下一步协方差矩阵 Pneg，然后使用这些估计值来计算最优增益矩阵 K 。 然后，通过比较真实观测值 z 和预测观测值 H*x 得到更新方程，从而计算出最终的状态估计 xe。   图3计算给定状态方程和观测矩阵的状态估计值 4、将先前4维状态空间模型变为一个3维的本质一维系统，并在此基础上实现了一维卡尔曼滤波器来进行状态估计。 - Phi1是原始Phi矩阵的3x3子矩阵，包含前3个状态变量的动态方程系数； - G1是控制向量，只包含对应于第三个状态的项； - H1是观测矩阵，只是取出用于测量第一个状态的项； - I1是3x3单位矩阵； - xel表示状态估计向量，内部仅包含3个状态变量； - Ppos1是初始误差协方差矩阵； 随后同之前，使用K和H1*xl计算当前状态的估计值以及Pest1中的各个状态估计误差。   图4 实现了卡尔曼滤波器来进行状态估计 5、实现了一个基于3个状态变量的本质一维卡尔曼滤波器，用来估计输入值（状态）和观测值。 具体来说，在每个时间步中，与之前类似，先利用当前时刻的协方差矩阵进行状态预测，并使用观测到的信息来更新误差协方差矩阵和状态估计向量。同时，还计算了最优增益矩阵K。 - x1(:,i)表示状态预测值； - Pneg1 是误差协方差的估计的先验（状态预测时）； - K1(:,i) 表示的是最优增益矩阵，用于将状态预测与观测值相结合以计算后验状态估计； - Ppos1 是误差协方差的后验（状态估计时）; - Pest1(:,1) 是Ppos1的第一个自由度（也就是对应的状态估计误差值）； 在每个时间步中，先进行状态预测，计算下一个x1，并利用先前的协方差矩阵计算提前估计的下一步协方差矩阵 Pneg1，然后使用这些估计值来计算最优增益矩阵 K1 。 然后，通过比较真实观测值 z 和预测观测值 H1*x1 得到更新方程，从而计算出最终的状态估计 xel。   图5 实现了一个基于3个状态变量的本质一维卡尔曼滤波器，用来估计输入值（状态）和观测值 6、用来计算状态估计与实际状态之间的误差，并使用折线图可视化结果。 - pos_diff表示状态扩展过程中位置的误差，即状态估计向量的第一个维度和真实状态向量的第一个维度之间的差异； - pos_diff1表示一维卡尔曼滤波器近似为白噪声模型时位置的误差； - pos_diff_m和pos_diff_s分别是状态扩展误差和近似误差在整个时间序列上的均值和标准差； - pos_diff_m1和pos_diff_s1是一维卡尔曼滤波器误差均值和标准差； - t是绘图所需的时间轴变量； - 第7行代码绘制了一个折线图，比较了两种方法（状态扩展和近似为白噪声）得到的位置误差随时间变化的情况； - legend函数用于添加数据标签； - xlabel和ylabel用于添加x，y轴标签。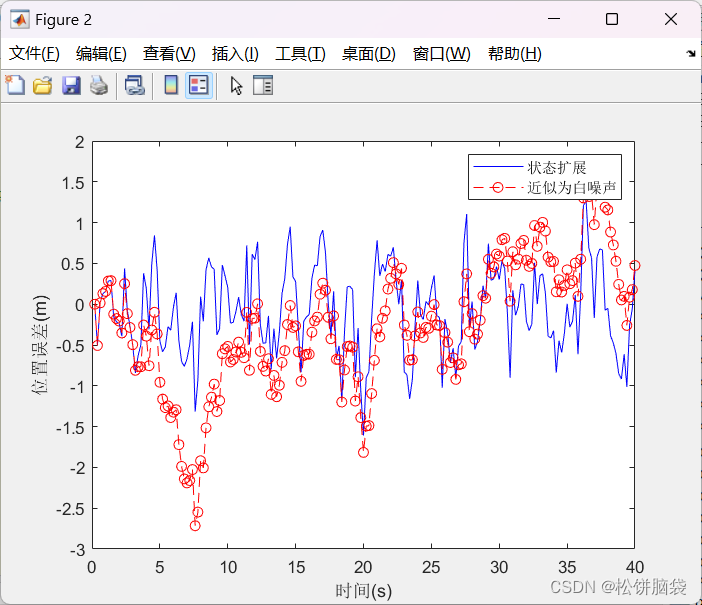   图6 结果绘制代码 7、实验结果图 扩展后的滤波估计误差均值和标准差分别为一0.0038和0.475 1,而将状态噪声按白噪声处理滤波估计的误差均值和标准差分别为0.271 3和0.655 3。需要注意的是,每次运行时由于噪声发生了变化,具体数值会有变化,但趋势是一致的,即扩展后的滤波精度更高,这与其理论最优性也是相符的。   图7 4-1实验结果图 实验4.2matlab程序代码 2.1、初始化几个变量，生成一个具有状态变量和观测模型的模拟线性动态系统。变量T表示时间步长，Q表示状态噪声方差，R表示测量噪声方差，N表示测量次数，a是用于产生测量噪声的参数。 代码将变量sigma设为Q的平方根，通过从均值为0、标准差为sigma的正态分布中采样产生状态噪声w，通过从均值为0、标准差为σ的另一个正态分布中采样产生测量噪声v，该正态分布等于根号R乘以(1-exp(-2*a*T))的平方根。最后，将变量Ps设为-a*T的指数，将测量噪声v的第一个元素赋给零向量v的第一个元素。   图8 定义变量 2.2、根据前一步中生成的测量值z估计系统的状态。 首先，转换后的测量向量z_star通过从当前测量中减去Ps乘以之前的测量来计算。然后，利用卡尔曼滤波方程对回路中每个时间步长的估计状态xe及其协方差矩阵Ppos进行更新和预测。在代码的第二部分，卡尔曼滤波器的一种变体被应用于基于时刻i的估计来预测时刻i+1的状态。这种方法被称为“一步提前”估计。其中，变量x1和xe1分别表示预测状态和估计状态，变量Ppre1、Pest1和Ppos1分别表示对应的协方差矩阵。 这些计算使用系统参数R和Q的修改版本，分别由R1和Qtemp表示。 图9  z估计系统的状态  2.3、计算系统位置组件的估计状态(xe)和真实状态(xr)之间的差异，同时使用标准卡尔曼滤波器和提前一步的变体。这些差异的均值和标准差被计算并存储在变量pos_diff_m、pos_diff_s、pos_diff_m1和pos_diff_s1中。 最后，使用plot函数创建位置误差作为两种估计方法的时间函数的图。   图10 4.2实验结果图