AVL树介绍、实现与封装

已于 2024-11-21 10:23:50 修改
阅读量1.1k 收藏 16
点赞数 24
分类专栏： 数据结构 文章标签： c++ 学习 AVL树 数据结构
于 2024-11-17 22:29:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq3304968099/article/details/143747120
版权

AVL树介绍、实现与封装

以下代码环境为 VS2022 C++。

一、AVL树的概念

AVL树 是最先发明的自平衡二叉搜索树。AVL树 是一颗空树，或具备下列性质的二叉搜索树：它的左右子树都是 AVL树，且左右子树的高度差的绝对值不超过 1。AVL树 是一颗高度平衡二叉搜索树，通过控制高度差去控制平衡。

AVL树 实现这里我们引入一个平衡因子(balance factor)的概念，每个节点都有一个平衡因子，任何节点的平衡因子等于右子树的高度减去左子树的高度，也就是说任何节点的平衡因子等于 0 / 1 / -1，AVL树 并不是必须要平衡因子，但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡。

AVL树 是高度平衡搜索二叉树，要求高度差不超过 1。注意有些情况是做不到高度差是 0 的，比如一棵树是 2 个节点，4 个节点等情况下，高度差最好就是 1，无法作为高度差是 0。

AVL树 整体节点数量和分布和完全二叉树类似，高度可以控制在 log N，那么增删查改的效率也可以控制在 O(logN)，相比二叉搜索树有了本质的提升。
在这里插入图片描述
在这里插入图片描述

二、AVL树的实现

1.AVL树的结构

template<class Key, class Value>
class AVLTree
{
	typedef std::pair<Key, Value> Type;

	struct AVLTreeNode
	{
		AVLTreeNode(const Type& data)
			:_data(data)
			, _left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _bf(0)
		{
			;
		}

		AVLTreeNode* _left;
		AVLTreeNode* _right;
		AVLTreeNode* _parent;	// 需要 _parent 指针，方便寻找
		Type _data;
		int _bf;				// 平衡因子
	};

	typedef AVLTreeNode Node;
	typedef Node* pNode;

	pNode _root = nullptr;
};

2.AVL树的插入

AVL树插入一个值的大概过程

  1. 插入一个值按二叉搜索树规则进行插入。

  2. 新增节点以后，只会影响祖先节点的高度，也就是可能会影响部分祖先节点的平衡因子，所以更新从新增节点 -> 根节点路径上的平衡因子，实际中最坏情况下要更新到根，有些情况更新到中间就可以停止了，具体情况下面再详细分析。

  3. 更新平衡因子过程中没有出现问题，则插入结束。

  4. 更新平衡因子过程中出现不平衡，对不平衡子树旋转，旋转后平衡的同时，本质降低了子树的高度，不会再影响上一层，所以插入结束。

平衡因子更新

更新原则：

  1. 平衡因子 = 右子树高度 - 左子树高度。

  2. 只有子树高度变化才会影响当前节点平衡因子。

  3. 插入节点，会增加高度，若新增节点在 parent 的右子树，parent 的平衡因子++，新增节点在 parent 的左子树，parent 的平衡因子 --。

  4. parent 所在子树的高度是否变化决定了是否会继续往上判断更新。

判断停止条件：

  1. 更新后 parent 的平衡因子等于 0，更新中 parent 的平衡因子变化为 -1 -> 0 或者 1 -> 0，说明更新前 parent 子树一边高一边低，新增的节点插入在低的那边，插入后 parent 所在的子树高度不变，不会影响 parent 的父亲节点的平衡因子，更新结束。

  2. 更新后 parent 的平衡因子等于 1 或 -1，更新中 parent 的平衡因子变化为 0 -> 1 或者 0 -> -1，说明更新前 parent 子树两边一样高，新增的插入节点后，parent 所在的子树一边高一边低，parent 所在的子树符合平衡要求，但是高度增加了 1，会影响 parent 的父亲节点的平衡因子，所以要继续向上更新。

  3. 更新后 parent 的平衡因子等于 2 或 -2，更新中 parent 的平衡因子变化为 1 -> 2 或者 -1 -> -2，说明更新前 parent 子树一边高一边低，新增的插入节点在高的那边，parent 所在的子树高的那边更高了，破坏了平衡，parent 所在的子树不符合平衡要求，需要旋转处理，旋转的目标有两个：把 parent 子树旋转平衡 和 降低 parent 子树的高度，恢复到插入节点以前的高度。所以旋转后也不需要继续往上更新，插入结束。

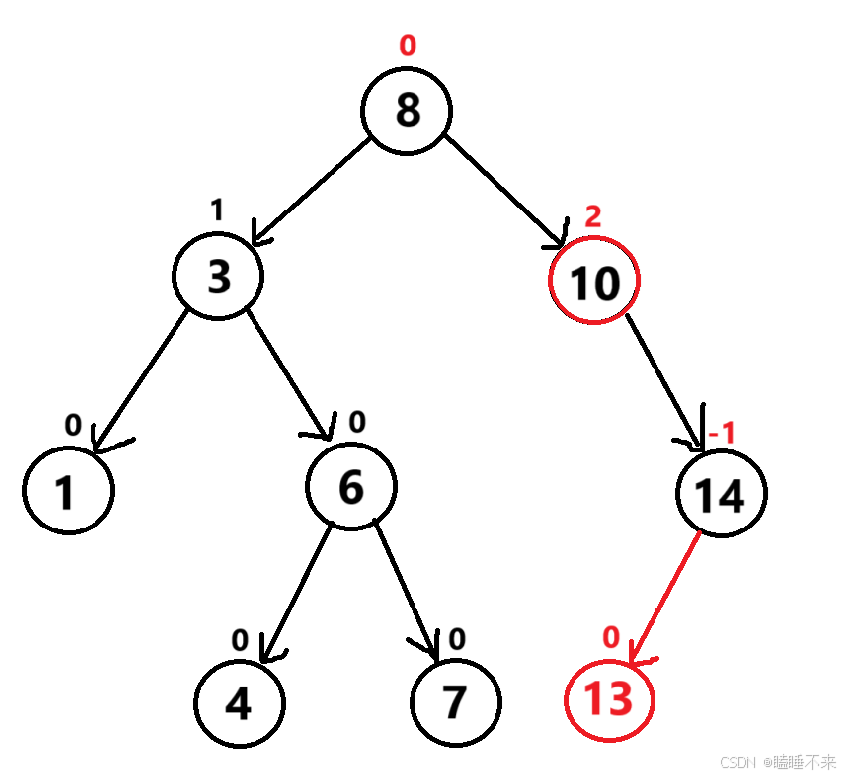
更新到 10 节点，平衡因子为 2，10 所在的子树已经不平衡，需要旋转处理
在这里插入图片描述

更新到中间节点，3 为根的子树高度不变，不会影响上一层，更新结束
在这里插入图片描述

最坏更新到根停止
在这里插入图片描述

插入节点及更新平衡因子的代码实现

bool insert(const Type& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		return true;
	}

	pNode parent = nullptr;
	pNode cur = _root;
	while (cur != nullptr)
	{
		if (cur->_data.first > data.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_data.first < data.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return false;
		}
	}

	// 插入
	pNode newNode = new Node(data);
	if (parent->_data.first > data.first)
	{
		parent->_left = newNode;
		--parent->_bf;
	}
	else
	{
		parent->_right = newNode;
		++parent->_bf;
	}
	newNode->_parent = parent;

	while (parent != nullptr)							// 更新平衡因子
	{
		if (parent->_bf == 0)							// 更新结束
		{
			break;
		}

		if (parent->_bf == 1 || parent->_bf == -1)		// 继续向上更新
		{
			pNode cur = parent;
			parent = parent->_parent;
			if (parent == nullptr)
			{
				;
			}
			else if (parent->_left == cur)
			{
				--parent->_bf;
			}
			else
			{
				++parent->_bf;
			}
		}
		else if (parent->_bf == -2)						// 不平衡旋转处理	
		{
			// ...
			break;
		}
		else											// 不平衡旋转处理	
		{
			// ...
			break;
		}
	}

	return true;
}

3.旋转

旋转的原则

  1. 保持搜索树的规则。

  2. 让旋转的树从不满足平衡变成满足平衡，其次降低树高度的旋转方式总共分为四种，左单旋 / 右单旋 / 左右双旋 / 右左双旋。

右单旋

  1. 下图展示的是 10 为根的树，有 a / b / c 抽象为三棵高度为 h 的子树(h>=0)，a / b / c 均符合 AVL树 的要求。10 可能是整棵树的根，也可能是一个整棵树中局部的子树的根。这里 a / b / c 是高度为 h 的子树，是一种概括抽象表示，其代表了所有右单旋的场景，实际右单旋形态有很多种，这里不做详细描述。

  2. 在 a 子树中插入一个新节点，导致 a 子树的高度从 h 变成 h + 1，不断向上更新平衡因子，导致 10 的平衡因子从 -1 变成 -2，10 为根的树左右高度差超过 1，违反平衡规则。10 为根的树左边太高了，需要往右边旋转，控制两棵树的平衡。

  3. 旋转核心步骤，因为 5 < b子树的值 < 10，将 b 变成 10 的左子树，10 变成 5 的右子树，5 变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的高度恢复到了插入之前的 h + 2，符合旋转原则。如果插入之前 10 整棵树的一个局部子树，旋转后不会再影响上一层，插入结束了。
    在这里插入图片描述

右单旋代码实现

	// 右单旋
	void rotateR(pNode parent)
	{
		pNode subL = parent->_left;
		pNode subLR = subL->_right;
		pNode pParent = parent->_parent;	// 需要注意除了要修改孩⼦指针指向，还有修改⽗亲
		
		parent->_left = subLR;
		if (subLR != nullptr)
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		parent->_parent = subL;

		subL->_parent = pParent;
		// parent有可能是整棵树的根，也可能是局部的⼦树
		// 如果是整棵树的根，要修改 _root
		// 如果是局部的指针要跟上⼀层链接
		if (pParent == nullptr)
		{
			_root = subL;
		}
		else if (pParent->_left == parent)
		{
			pParent->_left = subL;
		}
		else
		{
			pParent->_right = subL;
		}

		parent->_bf = subL->_bf = 0;
	}

左单旋

  1. 下图展示的是 10 为根的树，有 a / b / c 抽象为三棵高度为 h 的子树(h>=0)，a / b / c 均符合 AVL树 的要求。10 可能是整棵树的根，也可能是一个整棵树中局部的子树的根。这里 a / b / c 是高度为 h 的子树，是一种概括抽象表示，他代表了所有左单旋的场景，实际左单旋形态有很多种，具体跟上面右旋类似。

  2. 在 a 子树中插入一个新节点，导致 a 子树的高度从 h 变成 h + 1，不断向上更新平衡因子，导致 10 的平衡因子从 1 变成 2，10 为根的树左右高度差超过 1，违反平衡规则。10 为根的树右边太高了，需要往左边旋转，控制两棵树的平衡。

  3. 旋转核心步骤，因为 10 < b子树的值 < 15，将 b 变成 10 的右子树，10 变成 15 的左子树，15 变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的高度恢复到了插入之前的 h + 2，符合旋转原则。如果插入之前 10 整棵树的一个局部子树，旋转后不会再影响上一层，插入结束了。
    在这里插入图片描述

左单旋代码实现

	// 左单旋
	void rotateL(pNode parent)
	{
		pNode subR = parent->_right;
		pNode subRL = subR->_left;
		pNode pParent = parent->_parent;

		parent->_right = subRL;
		if (subRL != nullptr)
		{
			subRL->_parent = parent;
		}

		subR->_left = parent;
		parent->_parent = subR;

		subR->_parent = pParent;
		if (pParent == nullptr)
		{
			_root = subR;
		}
		else if (pParent->_left == parent)
		{
			pParent->_left = subR;
		}
		else
		{
			pParent->_right = subR;
		}

		parent->_bf = subR->_bf = 0;
	}

左右双旋

通过下图可以看到，左边高时，如果插入位置不是在 a 子树，而是插入在 b 子树，b 子树高度从 h 变成 h + 1，引发旋转，右单旋无法解决问题，右单旋后，我们的树依旧不平衡。右单旋解决的纯粹的左边高，但是插入在 b 子树中，10 为根的子树不再是单纯的左边高，对于 10 是左边高，但是对于 5 是右边高，需要用两次旋转才能解决，以 5 为旋转点进行一个左单旋，以 10 为旋转点进行一个右单旋，这棵树就平衡了。
在这里插入图片描述
在这里插入图片描述

下面我们将 a / b / c 子树抽象为高度 h 的 AVL子树 进行分析，另外我们需要把 b子树 的细节进一步展开为 8 和左子树高度为 h - 1 的 e 和 f 子树，因为我们要对 b 的父亲 5 为旋转点进行左单旋，左单旋需要动 b 树中的左子树。b 子树中新增节点的位置不同，平衡因子更新的细节也不同，通过观察 8 的平衡因子不同，这里我们要分三个情况讨论：

  1. 情况1：h >= 1 时，新增节点插入在 e 子树，e 子树高度从 h - 1 并为 h 并不断更新 8 -> 5 -> 10 平衡因子，引发旋转，其中 8 的平衡因子为 -1，旋转后 8 和 5 平衡因子为 0，10 平衡因子为 1。

  2. 情况2：h == 0 时，a / b / c 都是空树，b 自己就是一个新增节点，不断更新 5 -> 10 平衡因子，引发旋转，其中 8 的平衡因子为 0，旋转后 8 和 10 和 5 平衡因子均为 0。

  3. 情况3：h >= 1 时，新增节点插入在 f 子树，f 子树高度从 h - 1 变为 h 并不断更新 8 -> 5 -> 10 平衡因子，引发旋转，其中 8 的平衡因子为 1，旋转后 8 和 10 平衡因子为 0，5 平衡因子为 -1。
    在这里插入图片描述

左右双旋代码实现

	// 左右双旋
	void rotateLR(pNode parent)
	{
		pNode subL = parent->_left;
		pNode subLR = subL->_right;
		int bf = subLR->_bf;

		rotateL(parent->_left);		// 先子树左旋
		rotateR(parent);			// 再右旋

		if (bf == -1)
		{
			subL->_bf = 0;
			subLR->_bf = 0;
			parent->_bf = 1;
		}
		else if (bf == 1)
		{
			subL->_bf = -1;
			subLR->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			subL->_bf = 0;
			subLR->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

右左双旋

跟左右双旋类似，下面我们将 a / b / c 子树抽象为高度 h 的 AVL子树 进行分析，另外我们需要把 b 子树的细节进一步展开为 12 和左子树高度为 h - 1 的 e 和 f 子树，因为我们要对 b 的父亲 15 为旋转点进行右单旋，右单旋需要动 b 树中的右子树。b 子树中新增节点的位置不同，平衡因子更新的细节也不同，通过观察 12 的平衡因子不同，这里我们要分三个情况讨论：

  1. 情况1：h >= 1 时，新增节点插入在 f 子树，f 子树高度从 h - 1 变为 h 并不断更新 12 -> 15 -> 10 平衡因子，引发旋转，其中 12 的平衡因子为 1，旋转后 15 和 12 平衡因子为 0，10 平衡因子为 -1。

  2. 情况2：h == 0 时，a / b / c 都是空树，b 自己就是一个新增节点，不断更新 15 -> 10 平衡因子，引发旋转，其中 12 的平衡因子为 0，旋转后 10 和 12 和 15 平衡因子均为 0。

  3. 情况3：h >= 1 时，新增节点插入在 e 子树，e 子树高度从 h - 1 变为 h 并不断更新 12 -> 15 -> 10 平衡因子，引发旋转，其中 12 的平衡因子为 -1，旋转后 10 和 12 平衡因子为 0，15 平衡因子为 1。

在这里插入图片描述

右左双旋代码实现

	void rotateRL(pNode parent)
	{
		pNode subR = parent->_right;
		pNode subRL = subR->_left;
		int bf = subRL->_bf;

		rotateR(parent->_right);
		rotateL(parent);

		if (bf == -1)
		{
			subR->_bf = 1;
			subRL->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)
		{
			subR->_bf = 0;
			subRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == 0)
		{
			subR->_bf = 0;
			subRL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

4.AVL树的查找

按照二叉搜索树逻辑实现即可，搜索效率为 O(logN)

	pNode find(const Key& key)
	{
		pNode cur = _root;
		while (cur != nullptr)
		{
			if (cur->_data.first > key)
			{
				cur = cur->_left;
			}
			else if (cur->_data.first < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}

5.AVL树 插入平衡检测

我们实现的 AVL树的插入 是否合格，可以通过检查左右子树高度差的的程序进行反向验证，同时检查一下节点的平衡因子更新是否出现了问题。

	size_t _Height(pNode root)
	{
		if (root == nullptr)
		{
			return 0;
		}

		int leftHigh = _Height(root->_left);
		int rightHigh = _Height(root->_right);

		return (leftHigh > rightHigh ? leftHigh : rightHigh) + 1;
	}

	// 根据 AVL树 的概念验证其是否为有效的 AVL树
	bool _IsAVLTree(pNode root)
	{
		if (root == nullptr)		// 空树也是AVL树
		{
			return true;
		}

		// 计算 root 结点的平衡因⼦：即 root 左右⼦树的⾼度差
		int leftHigh = _Height(root->_left);
		int rightHigh = _Height(root->_right);
		int diff = rightHigh - leftHigh;

		// 如果计算出的平衡因⼦与 _root 的平衡因⼦不相等，
		// 或者 root 平衡因⼦的绝对值超过 1，则⼀定不是 AVL树
		if (abs(diff) >= 2)
		{
			std::cout << "高度差异常" << std::endl;
			return false;
		}
		else if (root->_bf != diff)
		{
			std::cout << "平衡因子异常" << std::endl;
			return false;
		}

		// root 的左和右如果都是 AVL树，则该树⼀定是 AVL树
		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
	}

void test1()
{
	AVLTree<int, int> t;
	// 常规的测试⽤例
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	// 特殊的带有双旋场景的测试⽤例
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		t.insert({ e, e });
	}
	t.inOrder();
	cout << endl;
	cout << t.isAVLTree() << endl;
}

// 插⼊⼀堆随机值，测试平衡，顺便测试⼀下⾼度和性能等
void test2()
{
	srand(time(0));
	const int N = 100000;

	vector<int> v;
	v.reserve(N);
	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
	}

	AVLTree<int, int> t;
	size_t begin2 = clock();
	for (auto e : v)
	{
		t.insert(make_pair(e, e));
	}
	size_t end2 = clock();

	cout << "insert:" << end2 - begin2 << endl;
	cout << t.isAVLTree() << endl;
	cout << "high:" << t.high() << endl;
	size_t begin1 = clock();
	// 确定在的值
	//for (auto e : v)
	//{
	//	t.find(e);
	//}
	// 随机值
	for (size_t i = 0; i < N; i++)
	{
		t.find((rand() + i));
	}
	size_t end1 = clock();
	cout << "find:" << end1 - begin1 << endl;
}

6.AVL树的删除

AVL树的删除使用的旋转依然是上面介绍的四种旋转情况，一些重复的介绍这里省略。

AVL树的删除可以借用二叉搜索树的删除，分为四种情况：

  1. 要删除节点 H 左右孩子均为空

  2. 要删除的节点 H 左孩子为空，右孩子节点不为空

  3. 要删除的节点 H 右孩子为空，左孩子节点不为空

  4. 要删除的节点 H 左右孩子节点均不为空

不过考虑到平衡因子的存在，我们需要对其具体分析。

左右孩子均为空的删除：

在这里插入图片描述

左孩子为空，右孩子节点不为空的删除：

在这里插入图片描述

右孩子为空，左孩子节点不为空的删除：

在这里插入图片描述

左右孩子节点均不为空：

我们使用替换法解决，在被删除节点的右孩子（或左孩子）开始，一直向下找到最小（或最大）的节点，然后交换两者数据。这里我采用从右孩子开始，向下找最小节点。

则对于第 4 种情况可以借用替换法转化成第 1 种情况 或 第 2 种情况：
在这里插入图片描述

平衡因子更新

AVL树的删除平衡因子更新考虑的情况更多：
在这里插入图片描述

删除代码实现

第 2 种情况与第 3 种情况不同之处只是连接的节点不同，这里合并在一起。

注意这里旋转后会将检查的 checkLevel 与 checkChild 位置改变，需要具体处理。

另外这里实现时先删除再将其进行平衡因子更新判断：

// N 表示空，H 表示有节点
// NN 表示 左右为空
// NH 表示 左为空	右有节点
// HN 表示 左有节点	右为空
void eraseNN(pNode& parent, pNode& aim, pNode& checkLevel, pNode& checkChild)
{
	if (parent == nullptr)							// 为空则根空
	{
		_root = nullptr;
	}
	else if (parent->_bf == 0)						// 不用向上判断
	{
		if (parent->_left == aim)
		{
			++parent->_bf;
			parent->_left = nullptr;
		}
		else
		{
			--parent->_bf;
			parent->_right = nullptr;
		}
	}
	else if (parent->_bf == 1)						// 平衡因子为 1				
	{
		if (parent->_left == aim)					// 为左
		{
			parent->_left = nullptr;

			if (parent->_right->_bf == 1)			// 左旋
			{
				rotateL(parent);

				checkChild = parent->_parent;		// 旋转后位置改变的处理，其他地方同理
				checkLevel = checkChild->_parent;
			}
			else if (parent->_right->_bf == -1)		// 右左旋
			{
				rotateRL(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
			else									// 左旋
			{
				rotateL(parent);					// 高度不变不用向上考虑

				parent->_bf = 1;					// 注意调整平衡因子
				parent->_parent->_bf = -1;
			}
		}
		else										// 为右
		{
			--parent->_bf;
			parent->_right = nullptr;

			checkChild = parent;
			checkLevel = checkChild->_parent;
		}
	}
	else											// 平衡因子为 -1
	{
		if (parent->_right == aim)					// 为右
		{
			parent->_right = nullptr;

			if (parent->_left->_bf == 1)			// 左右旋
			{
				rotateLR(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
			else if (parent->_left->_bf == -1)		// 右旋
			{
				rotateR(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
			else									// 右旋
			{
				rotateR(parent);					// 高度未变

				parent->_bf = -1;					// 调整平衡因子
				parent->_parent->_bf = 1;
			}
		}
		else										// 为左
		{
			++parent->_bf;
			parent->_left = nullptr;

			checkChild = parent;
			checkLevel = checkChild->_parent;
		}
	}
}

void erase_NH_or_HN(pNode& parent, pNode& aim, pNode& aimChild, pNode& checkLevel, pNode& checkChild)
{
	if (parent == nullptr)								// 删根节点
	{
		_root = aimChild;
		_root->_parent = nullptr;
	}
	else if (parent->_left == aim)						// 在左边
	{
		parent->_left = aimChild;
		aimChild->_parent = parent;

		if (parent->_bf == 1)
		{
			++parent->_bf;

			if (parent->_right->_bf == 1)				// 左旋
			{
				rotateL(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
			else if (parent->_right->_bf == 0)			// 左旋
			{
				rotateL(parent);						// 对高度不变，不用向上找

				parent->_bf = 1;						// 注意平衡因子
				parent->_parent->_bf = -1;
			}
			else										// 右左双旋
			{
				rotateRL(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
		}
		else if (parent->_bf == -1)						// 不用旋转
		{
			++parent->_bf;

			checkChild = parent;
			checkLevel = checkChild->_parent;
		}
		else											// parent 高度差为 0，调节完退出
		{
			++parent->_bf;
		}
	}
	else												// 在右边
	{
		parent->_right = aimChild;
		aimChild->_parent = parent;

		if (parent->_bf == 1)
		{
			--parent->_bf;

			checkChild = parent;
			checkLevel = checkChild->_parent;
		}
		else if (parent->_bf == -1)
		{
			--parent->_bf;

			if (parent->_left->_bf == 0)
			{
				rotateR(parent);					// 不用向上找

				parent->_bf = -1;
				parent->_parent->_bf = 1;
			}
			else if (parent->_left->_bf == 1)
			{
				rotateLR(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
			else
			{
				rotateR(parent);

				checkChild = parent->_parent;
				checkLevel = checkChild->_parent;
			}
		}
		else										// 此时 parent 高度差为 0
		{
			--parent->_bf;
		}
	}
}


bool erase(const Key& key)
{
	pNode aim = find(key);

	if (aim == nullptr)
	{
		return false;
	}

	pNode parent = aim->_parent;

	pNode checkChild = nullptr;
	pNode checkLevel = nullptr;

	// 先删除结点
	if (aim->_left == nullptr && aim->_right == nullptr)
	{
		eraseNN(parent, aim, checkLevel, checkChild);
	}
	else if (aim->_left == nullptr)
	{
		erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
	}
	else if (aim->_right == nullptr)
	{
		erase_NH_or_HN(parent, aim, aim->_left, checkLevel, checkChild);
	}
	else
	{
		pNode rightToLeft = aim->_right;
		pNode rightToLeftPrev = aim;
		while (rightToLeft != nullptr)					// 替换法
		{
			rightToLeftPrev = rightToLeft;
			rightToLeft = rightToLeft->_left;
		}

		std::swap(rightToLeftPrev->_data, aim->_data);	// 值交换

		pNode OtherNode = rightToLeftPrev->_right;

		int have_right = 0;
		if (OtherNode != nullptr)						// 判断右边是否为空
		{
			have_right = 1;
		}

		std::swap(rightToLeftPrev, aim);				// 指针交换
		parent = aim->_parent;							// parent 更新

		if (have_right == 0)							// 为 0 则是 第 1 种情况，反之为第 2 种情况
		{
			eraseNN(parent, aim, checkLevel, checkChild);
		}
		else
		{
			erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
		}
	}

	while (checkLevel != nullptr)						// 更新平衡因子
	{
		int child_is_left = checkLevel->_left == checkChild ? 1 : -1;

		if (checkLevel->_bf == 0)						// 停止更新
		{
			checkLevel->_bf += child_is_left;
			break;
		}
		else if (checkLevel->_bf == 1)
		{
			if (child_is_left == 1)						// 孩子为左
			{
				if (checkLevel->_right->_bf == 0)		// 高度整体不变
				{
					rotateL(checkLevel);
					checkLevel->_bf = 1;
					checkLevel->_parent->_bf = -1;
					break;
				}
				else if (checkLevel->_right->_bf == 1)
				{
					rotateL(checkLevel);

					checkChild = checkLevel;
					checkLevel = checkLevel->_parent;
				}
				else
				{
					rotateRL(checkLevel);

					checkChild = checkLevel;
					checkLevel = checkLevel->_parent;
				}
			}
			else										// 为右
			{
				checkLevel->_bf = 0;
			}
		}
		else
		{
			if (child_is_left == 1)						// 为左
			{
				checkLevel->_bf = 0;
			}
			else
			{
				if (checkLevel->_left->_bf == 0)		// 高度整体不变
				{
					rotateR(checkLevel);
					checkLevel->_bf = -1;
					checkLevel->_parent->_bf = 1;
					break;
				}
				else if (checkLevel->_left->_bf == 1)
				{
					rotateLR(checkLevel);

					checkChild = checkLevel;
					checkLevel = checkLevel->_parent;
				}
				else
				{
					rotateR(checkLevel);

					checkChild = checkLevel;
					checkLevel = checkLevel->_parent;
				}
			}
		}

		checkChild = checkLevel;						// 向上继续判断更新
		checkLevel = checkLevel->_parent;
	}

	delete aim;
	return true;
}

7.拷贝、遍历、销毁

拷贝与二叉树的先序遍历原理相同，遍历与二叉树的中序遍历相同，销毁与二叉树的后序遍历相同，这里不赘述。

		static void _inOrder(pNode root)				// 遍历等价为二叉树中序遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_inOrder(root->_left);
			std::cout << root->_data.second << ' ';
			_inOrder(root->_right);
		}

		static void _treeDestory(pNode root)			// 销毁等价为二叉树后续遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_treeDestory(root->_left);
			_treeDestory(root->_right);

			delete root;
		}
				// 使用这种方式拷贝注意使用引用，不然拷贝无效且导致内存泄漏
		static void _treeCopy(pNode& des, pNode src)	// 拷贝等价为二叉树先序遍历
		{
			if (src == nullptr)	
			{
				return;
			}

			des = new Node(src->_data);			
			des->_bf = src->_bf;

			_treeCopy(des->_left, src->_left);
			_treeCopy(des->_right, src->_right);

			if (des->_left != nullptr)			// 注意指向父亲结点
			{
				des->_left->_parent = des;
			}
			if (des->_right != nullptr)
			{
				des->_right->_parent = des;
			}
		}

三、AVL树的封装

注意到我们设计的只是 key / value 的 AVL树，还有 key 这种类型，这里将两者整合。

AVLTree_base

我们先将之前介绍的基础函数都封装到一个模版类，也就是 AVLTree_base 里方便后续 key / value 与 key 类型复用：

	template<class Type, class Key, class Value, class Node, class GetKey, class GetValue, class CompareKey>
	class AVLTree_base
	{
		typedef Node* pNode;

		pNode _root = nullptr;
		size_t _size = 0;

		static constexpr const GetKey _getKey = GetKey();
		static constexpr const GetValue _getValue = GetValue();
		static constexpr const CompareKey _comKey = CompareKey();

	protected:
		
		// N 表示空，H 表示有节点
		// NN 表示 左右为空
		// NH 表示 左为空	右有节点
		// HN 表示 左有节点	右为空
		void eraseNN(pNode& parent, pNode& aim, pNode& checkLevel, pNode& checkChild)
		{
			if (parent == nullptr)							// 为空则根空
			{
				_root = nullptr;
			}
			else if (parent->_bf == 0)						// 不用向上判断
			{
				if (parent->_left == aim)				
				{
					++parent->_bf;
					parent->_left = nullptr;
				}
				else									
				{
					--parent->_bf;
					parent->_right = nullptr;
				}
			}
			else if (parent->_bf == 1)						// 平衡因子为 1				
			{
				if (parent->_left == aim)					// 为左
				{
					parent->_left = nullptr;

					if (parent->_right->_bf == 1)			// 左旋
					{
						rotateL(parent);

						checkChild = parent->_parent;		// 旋转后位置改变的处理，其他地方同理
						checkLevel = checkChild->_parent;
					}
					else if (parent->_right->_bf == -1)		// 右左旋
					{
						rotateRL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else									// 左旋
					{
						rotateL(parent);					// 高度不变不用向上考虑

						parent->_bf = 1;					// 注意调整平衡因子
						parent->_parent->_bf = -1;
					}
				}
				else										// 为右
				{
					--parent->_bf;
					parent->_right = nullptr;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
			}
			else											// 平衡因子为 -1
			{
				if (parent->_right == aim)					// 为右
				{
					parent->_right = nullptr;

					if (parent->_left->_bf == 1)			// 左右旋
					{
						rotateLR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else if (parent->_left->_bf == -1)		// 右旋
					{
						rotateR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else									// 右旋
					{
						rotateR(parent);					// 高度未变

						parent->_bf = -1;					// 调整平衡因子
						parent->_parent->_bf = 1;
					}
				}
				else										// 为左
				{
					++parent->_bf;
					parent->_left = nullptr;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
			}
		}

		void erase_NH_or_HN(pNode& parent, pNode& aim, pNode& aimChild, pNode& checkLevel, pNode& checkChild)
		{
			if (parent == nullptr)								// 删根节点
			{
				_root = aimChild;
				_root->_parent = nullptr;
			}
			else if (parent->_left == aim)						// 在左边
			{
				parent->_left = aimChild;
				aimChild->_parent = parent;

				if (parent->_bf == 1)							
				{
					++parent->_bf;

					if (parent->_right->_bf == 1)				// 左旋
					{
						rotateL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else if (parent->_right->_bf == 0)			// 左旋
					{
						rotateL(parent);						// 对高度不变，不用向上找

						parent->_bf = 1;						// 注意平衡因子
						parent->_parent->_bf = -1;
					}
					else										// 右左双旋
					{
						rotateRL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
				}
				else if (parent->_bf == -1)						// 不用旋转
				{
					++parent->_bf;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
				else											// parent 高度差为 0，调节完退出
				{
					++parent->_bf;
				}
			}
			else												// 在右边
			{
				parent->_right = aimChild;
				aimChild->_parent = parent;

				if (parent->_bf == 1)							
				{
					--parent->_bf;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
				else if (parent->_bf == -1)
				{
					--parent->_bf;

					if (parent->_left->_bf == 0)			
					{
						rotateR(parent);					// 不用向上找

						parent->_bf = -1;
						parent->_parent->_bf = 1;
					}
					else if (parent->_left->_bf == 1)		
					{
						rotateLR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else
					{
						rotateR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
				}
				else										// 此时 parent 高度差为 0
				{
					--parent->_bf;
				}
			}
		}

	protected:

		void rotateR(pNode parent)					// 右单旋
		{
			pNode subL = parent->_left;
			pNode subLR = subL->_right;
			pNode pParent = parent->_parent;

			parent->_left = subLR;
			if (subLR != nullptr)
			{
				subLR->_parent = parent;
			}

			subL->_right = parent;
			parent->_parent = subL;

			subL->_parent = pParent;
			if (pParent == nullptr)
			{
				_root = subL;
			}
			else if (pParent->_left == parent)
			{
				pParent->_left = subL;
			}
			else
			{
				pParent->_right = subL;
			}

			parent->_bf = subL->_bf = 0;
		}

		void rotateL(pNode parent)		// 左单旋
		{
			pNode subR = parent->_right;
			pNode subRL = subR->_left;
			pNode pParent = parent->_parent;

			parent->_right = subRL;
			if (subRL != nullptr)
			{
				subRL->_parent = parent;
			}

			subR->_left = parent;
			parent->_parent = subR;

			subR->_parent = pParent;
			if (pParent == nullptr)
			{
				_root = subR;
			}
			else if (pParent->_left == parent)
			{
				pParent->_left = subR;
			}
			else
			{
				pParent->_right = subR;
			}

			parent->_bf = subR->_bf = 0;
		}

		void rotateRL(pNode parent)			// 右左双旋
		{
			pNode subR = parent->_right;
			pNode subRL = subR->_left;
			int bf = subRL->_bf;

			rotateR(parent->_right);		// 先子树右旋
			rotateL(parent);				// 再左旋

			if (bf == -1)
			{
				subR->_bf = 1;
				subRL->_bf = 0;
				parent->_bf = 0;
			}
			else if (bf == 1)
			{
				subR->_bf = 0;
				subRL->_bf = 0;
				parent->_bf = -1;
			}
			else
			{
				subR->_bf = 0;
				subRL->_bf = 0;
				parent->_bf = 0;
			}
		}

		void rotateLR(pNode parent)		// 左右双旋
		{
			pNode subL = parent->_left;
			pNode subLR = subL->_right;
			int bf = subLR->_bf;

			rotateL(parent->_left);
			rotateR(parent);

			if (bf == -1)
			{
				subL->_bf = 0;
				subLR->_bf = 0;
				parent->_bf = 1;
			}
			else if (bf == 1)
			{
				subL->_bf = -1;
				subLR->_bf = 0;
				parent->_bf = 0;
			}
			else
			{
				subL->_bf = 0;
				subLR->_bf = 0;
				parent->_bf = 0;
			}
		}

	protected:

		static size_t _height(pNode root)
		{
			if (root == nullptr)
			{
				return 0;
			}

			size_t leftHigh = _height(root->_left);
			size_t rightHigh = _height(root->_right);

			return (leftHigh > rightHigh ? leftHigh : rightHigh) + 1;
		}

		static bool _isAVLTree(pNode root)
		{
			if (root == nullptr)
			{
				return true;
			}

			int leftHigh = _height(root->_left);
			int rightHigh = _height(root->_right);

			int diff = rightHigh - leftHigh;
			if (abs(diff) >= 2)
			{
				std::cout << "高度差异常" << std::endl;
				return false;
			}
			else if (root->_bf != diff)
			{
				std::cout << "平衡因子异常" << std::endl;
				return false;
			}

			return _isAVLTree(root->_left) && _isAVLTree(root->_right);
		}

		static void _inOrder(pNode root)				// 遍历等价为二叉树中序遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_inOrder(root->_left);
			std::cout << _getValue(root->_data) << ' ';
			_inOrder(root->_right);
		}

		static void _treeDestory(pNode root)			// 销毁等价为二叉树后续遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_treeDestory(root->_left);
			_treeDestory(root->_right);

			delete root;
		}
				// 使用这种方式拷贝注意使用引用，不然拷贝无效且导致内存泄漏
		static void _treeCopy(pNode& des, pNode src)	// 拷贝等价为二叉树先序遍历
		{
			if (src == nullptr)	
			{
				return;
			}

			des = new Node(src->_data);			
			des->_bf = src->_bf;

			_treeCopy(des->_left, src->_left);
			_treeCopy(des->_right, src->_right);

			if (des->_left != nullptr)			// 注意指向父亲结点
			{
				des->_left->_parent = des;
			}
			if (des->_right != nullptr)
			{
				des->_right->_parent = des;
			}
		}

	protected:

		pNode _find(const Key& key) const
		{
			pNode cur = _root;
			while (cur != nullptr)
			{
				if (_comKey(_getKey(cur->_data), key) > 0)
				{
					cur = cur->_left;
				}
				else if (_comKey(_getKey(cur->_data), key) < 0)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}

		bool _insert(const Type& data)
		{
			if (_root == nullptr)
			{
				_root = new Node(data);
				return true;
			}

			pNode parent = nullptr;
			pNode cur = _root;
			while (cur != nullptr)
			{
				if (_comKey(_getKey(cur->_data), _getKey(data)) > 0)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (_comKey(_getKey(cur->_data), _getKey(data)) < 0)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}

			// 插入
			pNode newNode = new Node(data);
			if (_comKey(_getKey(parent->_data), _getKey(data)) > 0)
			{
				parent->_left = newNode;
				--parent->_bf;
			}
			else
			{
				parent->_right = newNode;
				++parent->_bf;
			}
			newNode->_parent = parent;

			while (parent != nullptr)
			{
				if (parent->_bf == 0)
				{
					break;
				}

				if (parent->_bf == 1 || parent->_bf == -1)
				{
					pNode cur = parent;
					parent = parent->_parent;
					if (parent == nullptr)
					{
						;
					}
					else if (parent->_left == cur)
					{
						--parent->_bf;
					}
					else
					{
						++parent->_bf;
					}
				}
				else if (parent->_bf == -2)
				{
					if (parent->_left->_bf == -1)
					{
						rotateR(parent);
					}
					else
					{
						rotateLR(parent);
					}
					break;
				}
				else
				{
					if (parent->_right->_bf == 1)
					{
						rotateL(parent);
					}
					else
					{
						rotateRL(parent);
					}
					break;
				}
			}

			return true;
		}

		bool _erase(const Key& key)
		{
			pNode aim = find(key);

			if (aim == nullptr)
			{
				return false;
			}

			pNode parent = aim->_parent;

			pNode checkChild = nullptr;
			pNode checkLevel = nullptr;

			// 先删除结点
			if (aim->_left == nullptr && aim->_right == nullptr)
			{
				eraseNN(parent, aim, checkLevel, checkChild);
			}
			else if (aim->_left == nullptr)
			{
				erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
			}
			else if (aim->_right == nullptr)
			{
				erase_NH_or_HN(parent, aim, aim->_left, checkLevel, checkChild);
			}
			else
			{
				pNode rightToLeft = aim->_right;
				pNode rightToLeftPrev = aim;
				while (rightToLeft != nullptr)					// 替换法
				{
					rightToLeftPrev = rightToLeft;
					rightToLeft = rightToLeft->_left;
				}

				std::swap(rightToLeftPrev->_data, aim->_data);	// 值交换

				pNode OtherNode = rightToLeftPrev->_right;

				int have_right = 0;
				if (OtherNode != nullptr)						// 判断右边是否为空
				{
					have_right = 1;
				}

				std::swap(rightToLeftPrev, aim);				// 指针交换
				parent = aim->_parent;							// parent 更新

				if (have_right == 0)							// 为 0 则是 第 1 种情况，反之为第 2 种情况
				{
					eraseNN(parent, aim, checkLevel, checkChild);
				}
				else
				{
					erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
				}
			}

			while (checkLevel != nullptr)						// 更新平衡因子
			{
				int child_is_left = checkLevel->_left == checkChild ? 1 : -1;

				if (checkLevel->_bf == 0)						// 停止更新
				{
					checkLevel->_bf += child_is_left;
					break;
				}
				else if (checkLevel->_bf == 1)					
				{
					if (child_is_left == 1)						// 孩子为左
					{
						if (checkLevel->_right->_bf == 0)		// 高度整体不变
						{
							rotateL(checkLevel);
							checkLevel->_bf = 1;
							checkLevel->_parent->_bf = -1;
							break;
						}
						else if (checkLevel->_right->_bf == 1)	
						{
							rotateL(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
						else
						{
							rotateRL(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
					}
					else										// 为右
					{
						checkLevel->_bf = 0;
					}
				}
				else
				{
					if (child_is_left == 1)						// 为左
					{
						checkLevel->_bf = 0;
					}
					else
					{
						if (checkLevel->_left->_bf == 0)		// 高度整体不变
						{
							rotateR(checkLevel);
							checkLevel->_bf = -1;
							checkLevel->_parent->_bf = 1;
							break;
						}
						else if (checkLevel->_left->_bf == 1)
						{
							rotateLR(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
						else
						{
							rotateR(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
					}
				}

				checkChild = checkLevel;						// 向上继续判断更新
				checkLevel = checkLevel->_parent;
			}

			delete aim;		
			return true;
		}

	public:

		AVLTree_base() = default;

		AVLTree_base(const AVLTree_base& tree)
		{
			_treeCopy(_root, tree._root);
			_size = tree._size;
		}

		AVLTree_base(AVLTree_base&& tree) noexcept
		{
			swap(tree);
		}

		AVLTree_base& operator=(AVLTree_base tree)
		{
			swap(tree);
			return *this;
		}

		AVLTree_base& operator=(AVLTree_base&& tree)
		{
			swap(tree);
			return *this;
		}

		~AVLTree_base()
		{
			if (_root != nullptr)
			{
				_treeDestory(_root);
			}
			_root = nullptr;
			_size = 0;
		}

		AVLTree_base(std::initializer_list<Type> list)
		{
			for (const Type& e : list)
			{
				insert(e);
			}
		}

		template<class InputIterator>
		AVLTree_base(InputIterator begin, InputIterator end)
		{
			while (begin != end)
			{
				insert(*begin);
				++begin;
			}
		}

	public:

		void swap(AVLTree_base& tree)
		{
			std::swap(_root, tree._root);
			std::swap(_size, tree._size);
		}

		pNode find(const Key& key) const
		{
			return _find(key);
		}

		bool insert(const Type& data)
		{
			bool access = _insert(data);
			if (access == true)
			{
				++_size;
			}
			return access;
		}

		bool erase(const Key& key)
		{
			if (_size == 0)
			{
				return false;
			}

			bool access = _erase(key);
			if (access == true)
			{
				--_size;
			}
			return access;
		}

		bool isAVLTree() const
		{
			return _isAVLTree(_root);
		}

		void inOrder() const
		{
			_inOrder(_root);
		}

		size_t high() const
		{
			return _height(_root);
		}

		size_t size() const
		{
			return _size;
		}
	};

key / value 复用

这里处理节点与 Key 和 Value 获取，将 AVLTree_base 组合为成员加上接口即可

	template<class Key, class Value, class CompareKey = less<Key>>
	class AVLTreeTwo
	{
		typedef std::pair<Key, Value> Type;

		struct AVLTreeNode							// key / value 节点
		{
			AVLTreeNode(const Type& data)
				:_data(data)
				, _left(nullptr)
				, _right(nullptr)
				, _parent(nullptr)
				, _bf(0)
			{
				;
			}

			AVLTreeNode* _left;
			AVLTreeNode* _right;
			AVLTreeNode* _parent;
			Type _data;
			int _bf;
		};

		typedef AVLTreeNode Node;
		typedef Node* pNode;
		typedef Node const* const_pNode;
		struct getMapKey							// 获取 Key
		{
			const Key& operator()(const Type& data) const
			{
				return data.first;
			}
		};
		struct getMapValue							// 获取 Value
		{
			const Value& operator()(const Type& data) const
			{
				return data.second;
			}
		};

		AVLTree_base<Type, Key, Value, Node, getMapKey, getMapValue, CompareKey> _base;

	public:

		AVLTreeTwo() = default;

		template<class InputIterator>
		AVLTreeTwo(InputIterator begin, InputIterator end)
			:_base(begin, end)
		{
			;
		}

		AVLTreeTwo(std::initializer_list<Type> list)
			:_base(list)
		{
			;
		}

		const const_pNode find(const Key& key) const	// 注意这里的 const_pNode 防止用户修改里边的内容
		{
			return _base.find(key);
		}

		bool insert(const Type& data)
		{
			return _base.insert(data);
		}

		bool erase(const Key& key)
		{
			return _base.erase(key);
		}

		bool isAVLTree() const
		{
			return _base.isAVLTree();
		}

		void inOrder() const
		{
			_base.inOrder();
		}

		size_t high() const
		{
			return _base.high();
		}

		size_t size() const
		{
			return _base.size();
		}
	};

key 复用

同上，这里处理节点与 Key 和 Value 获取，将 AVLTree_base 组合为成员加上接口即可：

	template<class T, class CompareKey = less<T>>
	class AVLTreeOne
	{
		typedef T Type;
		typedef T Key;
		typedef T Value;

		struct AVLTreeNode
		{
			AVLTreeNode(const Type& data = Type())
				: _left(nullptr)
				, _right(nullptr)
				, _parent(nullptr)
				, _data(data)
				, _bf(0)
			{
				;
			}

			AVLTreeNode* _left;
			AVLTreeNode* _right;
			AVLTreeNode* _parent;
			Type _data;
			int _bf;
		};

		typedef AVLTreeNode Node;
		typedef Node* pNode;
		typedef Node const* const_pNode;
		struct getSetKey
		{
			const Key& operator()(const Type& data) const
			{
				return data;
			}
		};
		struct getSetValue
		{
			const Key& operator()(const Type& data) const
			{
				return data;
			}
		};

		AVLTree_base<Type, Key, Value, Node, getSetKey, getSetValue, CompareKey> _base;

	public:

		AVLTreeOne() = default;

		template<class InputIterator>
		AVLTreeOne(InputIterator begin, InputIterator end)
			:_base(begin, end)
		{
			;
		}

		AVLTreeOne(std::initializer_list<Type> list)
			:_base(list)
		{
			;
		}

		const const_pNode find(const Key& key) const
		{
			return _base.find(key);
		}

		bool insert(const Type& data)
		{
			return _base.insert(data);
		}

		bool erase(const Key& key)
		{
			return _base.erase(key);
		}

		bool isAVLTree() const
		{
			return _base.isAVLTree();
		}

		void inOrder() const
		{
			_base.inOrder();
		}

		size_t high() const
		{
			return _base.high();
		}

		size_t size() const
		{
			return _base.size();
		}
	};

源码展示

#pragma once

#include <iostream>
#include <utility>
#include <cassert>

namespace my
{
	template<class Type, class Key, class Value, class Node, class GetKey, class GetValue, class CompareKey>
	class AVLTree_base
	{
		typedef Node* pNode;

		pNode _root = nullptr;
		size_t _size = 0;

		static constexpr const GetKey _getKey = GetKey();
		static constexpr const GetValue _getValue = GetValue();
		static constexpr const CompareKey _comKey = CompareKey();

	protected:
		
		// N 表示空，H 表示有节点
		// NN 表示 左右为空
		// NH 表示 左为空	右有节点
		// HN 表示 左有节点	右为空
		void eraseNN(pNode& parent, pNode& aim, pNode& checkLevel, pNode& checkChild)
		{
			if (parent == nullptr)							// 为空则根空
			{
				_root = nullptr;
			}
			else if (parent->_bf == 0)						// 不用向上判断
			{
				if (parent->_left == aim)				
				{
					++parent->_bf;
					parent->_left = nullptr;
				}
				else									
				{
					--parent->_bf;
					parent->_right = nullptr;
				}
			}
			else if (parent->_bf == 1)						// 平衡因子为 1				
			{
				if (parent->_left == aim)					// 为左
				{
					parent->_left = nullptr;

					if (parent->_right->_bf == 1)			// 左旋
					{
						rotateL(parent);

						checkChild = parent->_parent;		// 旋转后位置改变的处理，其他地方同理
						checkLevel = checkChild->_parent;
					}
					else if (parent->_right->_bf == -1)		// 右左旋
					{
						rotateRL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else									// 左旋
					{
						rotateL(parent);					// 高度不变不用向上考虑

						parent->_bf = 1;					// 注意调整平衡因子
						parent->_parent->_bf = -1;
					}
				}
				else										// 为右
				{
					--parent->_bf;
					parent->_right = nullptr;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
			}
			else											// 平衡因子为 -1
			{
				if (parent->_right == aim)					// 为右
				{
					parent->_right = nullptr;

					if (parent->_left->_bf == 1)			// 左右旋
					{
						rotateLR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else if (parent->_left->_bf == -1)		// 右旋
					{
						rotateR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else									// 右旋
					{
						rotateR(parent);					// 高度未变

						parent->_bf = -1;					// 调整平衡因子
						parent->_parent->_bf = 1;
					}
				}
				else										// 为左
				{
					++parent->_bf;
					parent->_left = nullptr;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
			}
		}

		void erase_NH_or_HN(pNode& parent, pNode& aim, pNode& aimChild, pNode& checkLevel, pNode& checkChild)
		{
			if (parent == nullptr)								// 删根节点
			{
				_root = aimChild;
				_root->_parent = nullptr;
			}
			else if (parent->_left == aim)						// 在左边
			{
				parent->_left = aimChild;
				aimChild->_parent = parent;

				if (parent->_bf == 1)							
				{
					++parent->_bf;

					if (parent->_right->_bf == 1)				// 左旋
					{
						rotateL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else if (parent->_right->_bf == 0)			// 左旋
					{
						rotateL(parent);						// 对高度不变，不用向上找

						parent->_bf = 1;						// 注意平衡因子
						parent->_parent->_bf = -1;
					}
					else										// 右左双旋
					{
						rotateRL(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
				}
				else if (parent->_bf == -1)						// 不用旋转
				{
					++parent->_bf;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
				else											// parent 高度差为 0，调节完退出
				{
					++parent->_bf;
				}
			}
			else												// 在右边
			{
				parent->_right = aimChild;
				aimChild->_parent = parent;

				if (parent->_bf == 1)							
				{
					--parent->_bf;

					checkChild = parent;
					checkLevel = checkChild->_parent;
				}
				else if (parent->_bf == -1)
				{
					--parent->_bf;

					if (parent->_left->_bf == 0)			
					{
						rotateR(parent);					// 不用向上找

						parent->_bf = -1;
						parent->_parent->_bf = 1;
					}
					else if (parent->_left->_bf == 1)		
					{
						rotateLR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
					else
					{
						rotateR(parent);

						checkChild = parent->_parent;
						checkLevel = checkChild->_parent;
					}
				}
				else										// 此时 parent 高度差为 0
				{
					--parent->_bf;
				}
			}
		}

	protected:

		void rotateR(pNode parent)					// 右单旋
		{
			pNode subL = parent->_left;
			pNode subLR = subL->_right;
			pNode pParent = parent->_parent;

			parent->_left = subLR;
			if (subLR != nullptr)
			{
				subLR->_parent = parent;
			}

			subL->_right = parent;
			parent->_parent = subL;

			subL->_parent = pParent;
			if (pParent == nullptr)
			{
				_root = subL;
			}
			else if (pParent->_left == parent)
			{
				pParent->_left = subL;
			}
			else
			{
				pParent->_right = subL;
			}

			parent->_bf = subL->_bf = 0;
		}

		void rotateL(pNode parent)		// 左单旋
		{
			pNode subR = parent->_right;
			pNode subRL = subR->_left;
			pNode pParent = parent->_parent;

			parent->_right = subRL;
			if (subRL != nullptr)
			{
				subRL->_parent = parent;
			}

			subR->_left = parent;
			parent->_parent = subR;

			subR->_parent = pParent;
			if (pParent == nullptr)
			{
				_root = subR;
			}
			else if (pParent->_left == parent)
			{
				pParent->_left = subR;
			}
			else
			{
				pParent->_right = subR;
			}

			parent->_bf = subR->_bf = 0;
		}

		void rotateRL(pNode parent)			// 右左双旋
		{
			pNode subR = parent->_right;
			pNode subRL = subR->_left;
			int bf = subRL->_bf;

			rotateR(parent->_right);		// 先子树右旋
			rotateL(parent);				// 再左旋

			if (bf == -1)
			{
				subR->_bf = 1;
				subRL->_bf = 0;
				parent->_bf = 0;
			}
			else if (bf == 1)
			{
				subR->_bf = 0;
				subRL->_bf = 0;
				parent->_bf = -1;
			}
			else
			{
				subR->_bf = 0;
				subRL->_bf = 0;
				parent->_bf = 0;
			}
		}

		void rotateLR(pNode parent)		// 左右双旋
		{
			pNode subL = parent->_left;
			pNode subLR = subL->_right;
			int bf = subLR->_bf;

			rotateL(parent->_left);
			rotateR(parent);

			if (bf == -1)
			{
				subL->_bf = 0;
				subLR->_bf = 0;
				parent->_bf = 1;
			}
			else if (bf == 1)
			{
				subL->_bf = -1;
				subLR->_bf = 0;
				parent->_bf = 0;
			}
			else
			{
				subL->_bf = 0;
				subLR->_bf = 0;
				parent->_bf = 0;
			}
		}

	protected:

		static size_t _height(pNode root)
		{
			if (root == nullptr)
			{
				return 0;
			}

			size_t leftHigh = _height(root->_left);
			size_t rightHigh = _height(root->_right);

			return (leftHigh > rightHigh ? leftHigh : rightHigh) + 1;
		}

		static bool _isAVLTree(pNode root)
		{
			if (root == nullptr)
			{
				return true;
			}

			int leftHigh = _height(root->_left);
			int rightHigh = _height(root->_right);

			int diff = rightHigh - leftHigh;
			if (abs(diff) >= 2)
			{
				std::cout << "高度差异常" << std::endl;
				return false;
			}
			else if (root->_bf != diff)
			{
				std::cout << "平衡因子异常" << std::endl;
				return false;
			}

			return _isAVLTree(root->_left) && _isAVLTree(root->_right);
		}

		static void _inOrder(pNode root)				// 遍历等价为二叉树中序遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_inOrder(root->_left);
			std::cout << _getValue(root->_data) << ' ';
			_inOrder(root->_right);
		}

		static void _treeDestory(pNode root)			// 销毁等价为二叉树后续遍历
		{
			if (root == nullptr)
			{
				return;
			}

			_treeDestory(root->_left);
			_treeDestory(root->_right);

			delete root;
		}
				// 使用这种方式拷贝注意使用引用，不然拷贝无效且导致内存泄漏
		static void _treeCopy(pNode& des, pNode src)	// 拷贝等价为二叉树先序遍历
		{
			if (src == nullptr)	
			{
				return;
			}

			des = new Node(src->_data);			
			des->_bf = src->_bf;

			_treeCopy(des->_left, src->_left);
			_treeCopy(des->_right, src->_right);

			if (des->_left != nullptr)			// 注意指向父亲结点
			{
				des->_left->_parent = des;
			}
			if (des->_right != nullptr)
			{
				des->_right->_parent = des;
			}
		}

	protected:

		pNode _find(const Key& key) const
		{
			pNode cur = _root;
			while (cur != nullptr)
			{
				if (_comKey(_getKey(cur->_data), key) > 0)
				{
					cur = cur->_left;
				}
				else if (_comKey(_getKey(cur->_data), key) < 0)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}

		bool _insert(const Type& data)
		{
			if (_root == nullptr)
			{
				_root = new Node(data);
				return true;
			}

			pNode parent = nullptr;
			pNode cur = _root;
			while (cur != nullptr)
			{
				if (_comKey(_getKey(cur->_data), _getKey(data)) > 0)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (_comKey(_getKey(cur->_data), _getKey(data)) < 0)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}

			// 插入
			pNode newNode = new Node(data);
			if (_comKey(_getKey(parent->_data), _getKey(data)) > 0)
			{
				parent->_left = newNode;
				--parent->_bf;
			}
			else
			{
				parent->_right = newNode;
				++parent->_bf;
			}
			newNode->_parent = parent;

			while (parent != nullptr)
			{
				if (parent->_bf == 0)
				{
					break;
				}

				if (parent->_bf == 1 || parent->_bf == -1)
				{
					pNode cur = parent;
					parent = parent->_parent;
					if (parent == nullptr)
					{
						;
					}
					else if (parent->_left == cur)
					{
						--parent->_bf;
					}
					else
					{
						++parent->_bf;
					}
				}
				else if (parent->_bf == -2)
				{
					if (parent->_left->_bf == -1)
					{
						rotateR(parent);
					}
					else
					{
						rotateLR(parent);
					}
					break;
				}
				else
				{
					if (parent->_right->_bf == 1)
					{
						rotateL(parent);
					}
					else
					{
						rotateRL(parent);
					}
					break;
				}
			}

			return true;
		}

		bool _erase(const Key& key)
		{
			pNode aim = find(key);

			if (aim == nullptr)
			{
				return false;
			}

			pNode parent = aim->_parent;

			pNode checkChild = nullptr;
			pNode checkLevel = nullptr;

			// 先删除结点
			if (aim->_left == nullptr && aim->_right == nullptr)
			{
				eraseNN(parent, aim, checkLevel, checkChild);
			}
			else if (aim->_left == nullptr)
			{
				erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
			}
			else if (aim->_right == nullptr)
			{
				erase_NH_or_HN(parent, aim, aim->_left, checkLevel, checkChild);
			}
			else
			{
				pNode rightToLeft = aim->_right;
				pNode rightToLeftPrev = aim;
				while (rightToLeft != nullptr)					// 替换法
				{
					rightToLeftPrev = rightToLeft;
					rightToLeft = rightToLeft->_left;
				}

				std::swap(rightToLeftPrev->_data, aim->_data);	// 值交换

				pNode OtherNode = rightToLeftPrev->_right;

				int have_right = 0;
				if (OtherNode != nullptr)						// 判断右边是否为空
				{
					have_right = 1;
				}

				std::swap(rightToLeftPrev, aim);				// 指针交换
				parent = aim->_parent;							// parent 更新

				if (have_right == 0)							// 为 0 则是 第 1 种情况，反之为第 2 种情况
				{
					eraseNN(parent, aim, checkLevel, checkChild);
				}
				else
				{
					erase_NH_or_HN(parent, aim, aim->_right, checkLevel, checkChild);
				}
			}

			while (checkLevel != nullptr)						// 更新平衡因子
			{
				int child_is_left = checkLevel->_left == checkChild ? 1 : -1;

				if (checkLevel->_bf == 0)						// 停止更新
				{
					checkLevel->_bf += child_is_left;
					break;
				}
				else if (checkLevel->_bf == 1)					
				{
					if (child_is_left == 1)						// 孩子为左
					{
						if (checkLevel->_right->_bf == 0)		// 高度整体不变
						{
							rotateL(checkLevel);
							checkLevel->_bf = 1;
							checkLevel->_parent->_bf = -1;
							break;
						}
						else if (checkLevel->_right->_bf == 1)	
						{
							rotateL(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
						else
						{
							rotateRL(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
					}
					else										// 为右
					{
						checkLevel->_bf = 0;
					}
				}
				else
				{
					if (child_is_left == 1)						// 为左
					{
						checkLevel->_bf = 0;
					}
					else
					{
						if (checkLevel->_left->_bf == 0)		// 高度整体不变
						{
							rotateR(checkLevel);
							checkLevel->_bf = -1;
							checkLevel->_parent->_bf = 1;
							break;
						}
						else if (checkLevel->_left->_bf == 1)
						{
							rotateLR(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
						else
						{
							rotateR(checkLevel);

							checkChild = checkLevel;
							checkLevel = checkLevel->_parent;
						}
					}
				}

				checkChild = checkLevel;						// 向上继续判断更新
				checkLevel = checkLevel->_parent;
			}

			delete aim;		
			return true;
		}

	public:

		AVLTree_base() = default;

		AVLTree_base(const AVLTree_base& tree)
		{
			_treeCopy(_root, tree._root);
			_size = tree._size;
		}

		AVLTree_base(AVLTree_base&& tree) noexcept
		{
			swap(tree);
		}

		AVLTree_base& operator=(AVLTree_base tree)
		{
			swap(tree);
			return *this;
		}

		AVLTree_base& operator=(AVLTree_base&& tree)
		{
			swap(tree);
			return *this;
		}

		~AVLTree_base()
		{
			if (_root != nullptr)
			{
				_treeDestory(_root);
			}
			_root = nullptr;
			_size = 0;
		}

		AVLTree_base(std::initializer_list<Type> list)
		{
			for (const Type& e : list)
			{
				insert(e);
			}
		}

		template<class InputIterator>
		AVLTree_base(InputIterator begin, InputIterator end)
		{
			while (begin != end)
			{
				insert(*begin);
				++begin;
			}
		}

	public:

		void swap(AVLTree_base& tree)
		{
			std::swap(_root, tree._root);
			std::swap(_size, tree._size);
		}

		pNode find(const Key& key) const
		{
			return _find(key);
		}

		bool insert(const Type& data)
		{
			bool access = _insert(data);
			if (access == true)
			{
				++_size;
			}
			return access;
		}

		bool erase(const Key& key)
		{
			if (_size == 0)
			{
				return false;
			}

			bool access = _erase(key);
			if (access == true)
			{
				--_size;
			}
			return access;
		}

		bool isAVLTree() const
		{
			return _isAVLTree(_root);
		}

		void inOrder() const
		{
			_inOrder(_root);
		}

		size_t high() const
		{
			return _height(_root);
		}

		size_t size() const
		{
			return _size;
		}
	};

	template<class Key>
	struct less
	{
		int operator()(const Key& one, const Key& two) const
		{
			if (one < two)
			{
				return -1;
			}
			else if (one > two)
			{
				return 1;
			}
			return 0;
		}
	};
	template<class Key>
	struct greater
	{
		int operator()(const Key& one, const Key& two) const
		{
			if (one < two)
			{
				return 1;
			}
			else if (one > two)
			{
				return -1;
			}
			return 0;
		}
	};

	template<class T, class CompareKey = less<T>>
	class AVLTreeOne
	{
		typedef T Type;
		typedef T Key;
		typedef T Value;

		struct AVLTreeNode
		{
			AVLTreeNode(const Type& data = Type())
				: _left(nullptr)
				, _right(nullptr)
				, _parent(nullptr)
				, _data(data)
				, _bf(0)
			{
				;
			}

			AVLTreeNode* _left;
			AVLTreeNode* _right;
			AVLTreeNode* _parent;
			Type _data;
			int _bf;
		};

		typedef AVLTreeNode Node;
		typedef Node* pNode;
		typedef Node const* const_pNode;
		struct getSetKey
		{
			const Key& operator()(const Type& data) const
			{
				return data;
			}
		};
		struct getSetValue
		{
			const Key& operator()(const Type& data) const
			{
				return data;
			}
		};

		AVLTree_base<Type, Key, Value, Node, getSetKey, getSetValue, CompareKey> _base;

	public:

		AVLTreeOne() = default;

		template<class InputIterator>
		AVLTreeOne(InputIterator begin, InputIterator end)
			:_base(begin, end)
		{
			;
		}

		AVLTreeOne(std::initializer_list<Type> list)
			:_base(list)
		{
			;
		}

		const const_pNode find(const Key& key) const
		{
			return _base.find(key);
		}

		bool insert(const Type& data)
		{
			return _base.insert(data);
		}

		bool erase(const Key& key)
		{
			return _base.erase(key);
		}

		bool isAVLTree() const
		{
			return _base.isAVLTree();
		}

		void inOrder() const
		{
			_base.inOrder();
		}

		size_t high() const
		{
			return _base.high();
		}

		size_t size() const
		{
			return _base.size();
		}
	};

	template<class Key, class Value, class CompareKey = less<Key>>
	class AVLTreeTwo
	{
		typedef std::pair<Key, Value> Type;

		struct AVLTreeNode							// key / value 节点
		{
			AVLTreeNode(const Type& data)
				:_data(data)
				, _left(nullptr)
				, _right(nullptr)
				, _parent(nullptr)
				, _bf(0)
			{
				;
			}

			AVLTreeNode* _left;
			AVLTreeNode* _right;
			AVLTreeNode* _parent;
			Type _data;
			int _bf;
		};

		typedef AVLTreeNode Node;
		typedef Node* pNode;
		typedef Node const* const_pNode;
		struct getMapKey							// 获取 Key
		{
			const Key& operator()(const Type& data) const
			{
				return data.first;
			}
		};
		struct getMapValue							// 获取 Value
		{
			const Value& operator()(const Type& data) const
			{
				return data.second;
			}
		};

		AVLTree_base<Type, Key, Value, Node, getMapKey, getMapValue, CompareKey> _base;

	public:

		AVLTreeTwo() = default;

		template<class InputIterator>
		AVLTreeTwo(InputIterator begin, InputIterator end)
			:_base(begin, end)
		{
			;
		}

		AVLTreeTwo(std::initializer_list<Type> list)
			:_base(list)
		{
			;
		}

		const const_pNode find(const Key& key) const	// 注意这里的 const_pNode 防止用户修改里边的内容
		{
			return _base.find(key);
		}

		bool insert(const Type& data)
		{
			return _base.insert(data);
		}

		bool erase(const Key& key)
		{
			return _base.erase(key);
		}

		bool isAVLTree() const
		{
			return _base.isAVLTree();
		}

		void inOrder() const
		{
			_base.inOrder();
		}

		size_t high() const
		{
			return _base.high();
		}

		size_t size() const
		{
			return _base.size();
		}
	};
}
AVL
zhoutonglx的专栏
08-11 365
reference: 数据结构 邓俊辉 第三版#include<iostream> using std::swap; using std::cout; using std::cin; using std::endl; using std::max; #define pnode node* #define isRoot(x) (!((x).parent)) #define isLChild(x) (!
AVL树
晴天的专栏
03-19 875
1. 概述 AVL树是最早提出的自平衡二叉树，在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis。AVL树种查找、插入和删除在平均和最坏情况下都是O（log n），增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。本文介绍了AVL树的设计思想和基本操作。 2. 基本术语 有四
AVL树的操作
myBarbell的博客
04-01 536
AVL（ Adelson-Velsky and Landis）树是一棵自平衡的二叉查找树BST（binary search tree），所谓二叉查找树就是：左子树结点值&lt;根节点值&lt;右子树结点值。在查找结点值时相对普通二叉树的查找可以进行剪枝处理，当待查找值小于当前结点值时，往左子树查找，当待查结点值大于当前结点值时往右子树查找，这样查找时总体能达到o(logn)的复杂度。但当二叉查找树...
【数据结构与算法】【15】AVL树
天天向上 Up Up Up (*^▽^*)
07-19 888
AVL树的删除和插入基本类似，由于AVL树本来就是高度平衡的，删除一个元素只会影响到parent节点的平衡因子。对于第二种情况，则需要向上递归，更新parent的parent的平衡因子，直到某个parent的平衡因子为0。AVL树的优点在于，查询效率很高，但要维护其平衡性，在插入时需要进行一些转换，这样就会导致其插入效率比较低。判断删除后，parent节点的平衡因子是否大于1，如果大于1，按照一样的方法进行旋转即可。可以看出，最终的树结构和环境因子，和我们上面图示的情况一模一样，完全正确。.........
数据结构_算法实现_Java_AVL树_学习与优化应用_1741873056.zip
最新发布
03-15
本文档《数据结构_算法实现_Java_AVL树_学习与优化应用_1741873056.zip》包含了一系列关于AVL树在Java中实现的学习资源，这些资源有助于读者深入理解AVL树的原理、操作方法以及性能优化技巧。文档可能包含了详细的...
C++ AVL树的实现
07-10
AVL树是一种自平衡二叉查找树（Binary Search Tree，...以上是C++实现AVL树的基础知识点，具体实现过程会涉及更多细节，如旋转的具体代码实现、错误处理等。在实际编码时，还需要注意C++语法和面向对象设计原则的运用。
C语言实现AVL树封装类教程：初始化及增删操作
7. Visual C++中的AVL树实现： - 在Visual C++中实现AVL树时，可以使用类模板来增强代码的通用性和复用性。 - 实现过程中需要特别注意内存的管理，如动态分配和释放节点内存。 8. AVL树的实际应用： - AVL树适用...
掌握基础：AVL树、Splay树与二叉搜索树的实现代码
从提供的文件名称列表“AVLtree、BSTtree、Splay_tree”中，我们可以看到代码实现了AVL树、二叉搜索树和splay树。这些文件可能包含了每个数据结构的定义、节点类、树的操作（如插入、删除、查找）以及可能的自平衡或...
AVL树的C++实现
05-01
本文档详细介绍了一个完整的AVL树C++实现案例。AVL树是一种自平衡二叉搜索树，它由Georgy Adelson-Velsky和Evgenii Landis在1962年提出。AVL树的特点在于任何节点的两个子树的高度最大差别不超过1，这保证了AVL树的...
AVL（平衡二叉树）
weixin_41027614的博客
07-09 235
#include&lt;iostream&gt; #include&lt;cmath&gt; using namespace std; const int MAXSIZE=100; const int LH=1,EH=0,RH=-1; /*左高,等高,右高*/ /*二叉树的二叉链表结点结构定义*/ typedef struct BiTNode /*结点结构*/ { int data;...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值