图（二）---------图的深度优先遍历算法和广度优先遍历算法

今天我来介绍一些图的深度优先遍历算法和广度优先遍历算法。在展示我的代码之前我想先对这两种算法进行一些讲述

首先是深度优先遍历算法。

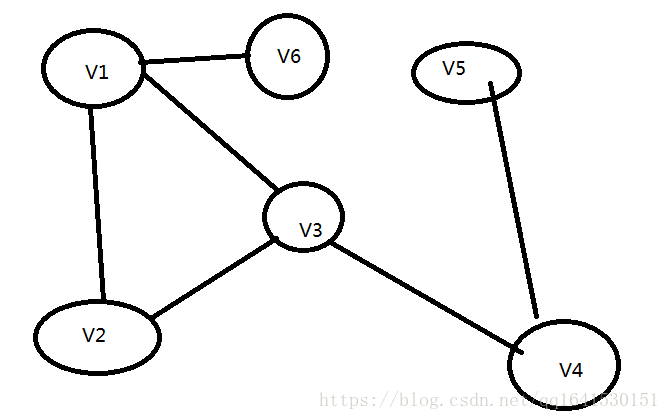
大家来看这个图，深度优先遍历就是以一个顶点为起点，找到它的第一个邻接顶点并将这个顶点设置为已经访问过的，然后递归之前的方法，直到所有的顶点的第一个邻接点都被访问过了。然后向上回溯，查找其他的邻接顶点重复之前的方法查找其他的邻接顶点的第一个邻接顶点是否被访问。

以我这个图为例首先访问V1,然后它的第一个邻接顶点是V2，然后是V3，V4。遍历到V5时，由于V5没有邻接顶点，所以向上回溯，直到回溯到V1，查找到V6。

下面我来解释一下我的代码

为了防止重复被访问，我设置了一个数组

private boolean[] isVisited;// 判断顶点是否被访问过的数组

public void depthFirstSearch(int i) {
		System.out.println("访问到了" + i + "结点");
		for (int j = 0; j < vertexSize; j++) {
			isVisited[i] = true;
			if (matrix[i][j] != 0 && matrix[i][j] != MAX_WEIGHT && !isVisited[j]) {
				isVisited[j] = true;
				depthFirstSearch(j);
			}
		}
	}

可以看到我的代码基本上就是我的思路的一个实现。只有该顶点未被访问过时，才会去递归调用我的depthFirstSearch算法。

图的广度优先遍历算法，很像我们在二叉树中遇到的层次遍历，其原理是先将每第一个顶点的所有邻接顶点都访问一遍将其设置为已经访问状态，然后将其入队。然后从队头元素开始遍历队头元素的所有未被访问过的邻接顶点，将未被访问的邻接顶点入队并将其设置为已经访问状态。直到队列空。

public void breadFirstSearch(int i) {
		Queue<Integer> queue = new LinkedList<Integer>();
		for (int j = 0; j < vertexSize; j++) {
			if (matrix[i][j] != MAX_WEIGHT && !isVisited[j]) {
				System.out.println("访问到了" + j + "结点");
				isVisited[j] = true;
				if (j != i) {
					queue.add(j);
				}
			}
		}
		while (!queue.isEmpty()) {
			breadFirstSearch(queue.remove());
		}
	}

算法如上，其实刚开始时这两个算法让我很头疼，但是当我们梳理清楚其中的原理，实际上也可以将这些算法很好写出。