二分搜索(c++,模板，详细解析)

普通二分搜索

while(l<r)的情况

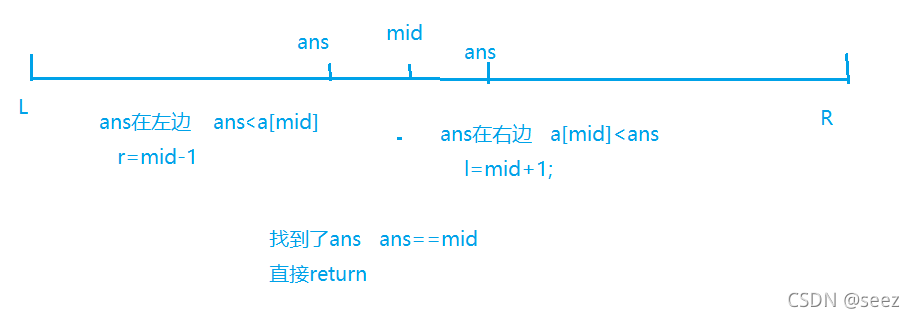
循环条件                初始化                循环终止                查询区间

 while(l<r)                l=0，r=n             l==r                        [l,r)

while(l<=r)               l=0,r=n-1            l==r+1                    [l,r]

int binary_search(int x)
{//普通二叉搜索，查找某个元素，返回下标
	int l = 0;
	int r = n;			//数组长度
	//l<r,循环终止条件是l==r,可遍历区间是[l,r)
	while (l < r)
	{
		int mid = l + r >> 1;		//中点
		if (a[mid] == x)
			return mid;
		else if (a[mid] < x)				//x在mid右边
			l = mid + 1;				//去区间[mid+1,r)寻找
		else if (a[mid] > x)			//x在mid左边
			r = mid;					//去区间[l,mid)寻找
	}
	//最后出来时l==r，我们少检查一个元素mid，此时还要检查
	return a[l]==x?l:-1;							//找不到

	/*以下是方法二*/
	 l = 0;
	 r = n - 1;
	//l<=r,循环终止条件是l==r+1,可遍历区间是[l,r]
	//由于右边会取交集，所以r==n-1，而不是取n
	while (l <= r)
	{
		int mid = l + r >> 1;
		if (a[mid] == x)
			return mid;
		else if (a[mid] < x)		//right
			l = mid + 1;			//去区间[mid+1,r]寻找
		else if (a[mid] > x)			//left
			r = mid - 1;			//去区间[l,mid-1]寻找
	}
	return -1;
	//l<=r退出的循环条件是l==r+1，等价于[r+1,r]，所以是不会漏的
	//那么如果while循环找不到，就说明没有
}

如果一个x有多个，二分搜索分为两种情况：

1.寻找第一个满足条件的元素

2.寻找最后一个满足条件的元素

1.寻找第一个满足条件的元素

int left_bound(int x)
{//寻找x的第一个出现的下标
//也可以理解为：数组中有几个小于x的数字，可能的返回值取值为[0,n]

	int l = 0, r = n;
	//l<r   搜索区间[l,r),终止条件l==r
	while (l < r)			
	{
		int mid = l + r >> 1;
		if (a[mid] < x)	//元素在右边
			l = mid + 1;	//去[mid+1,r)区间寻找
		else if (a[mid] > x)	//元素在左边
			r = mid;	//去[l,mid)区间寻找
		else if (a[mid] == x)	//这也是为什么能搜查左边界的原因
			//遇到x时不是立即返回，而是继续向左搜索，减小右边边界
			r = mid;
	}
	//循环终止条件是l==r，可能取值是[0,n]，left满足时返回l,当搜寻不到时返回-1
	//可能越界，先检查是否越界
	if (l == n) return -1;
	return a[l] == x ? l : -1;

	//方法二，while(l<=r)的情况
	 l = 0, r = n - 1;
	//l<=r  搜索区间
	 while (l <= r)
	 {
		 int mid = l + r >> 1;
		 if (a[mid] < x)		//x在右边
			 l = mid + 1;		//去[mid+1,r]区间查找
		 else if (a[mid] > x)	//x在左边
			 r = mid - 1;		//去[l,mid-1]区间查找
		 else if (a[mid] == x)
			 r = mid - 1;		//去[l,mid-1]区间查找
	 }
	 //由于循环终止条件是  l==r+1  l可能取值是[0,n]
	 //由于l可能取到n，下标会越界，所以需要检查
	 if (l >= n || a[l] != x)
		 return -1;
	 return l;
}
/*搜索右侧边界的时候，l需要-1，而搜索左侧边界却不用
答：while(l<r)时，搜索左侧边界，r=mid，最后循环终止l==r，如果仅有一个x，也确定会找到
    while(l<=r)时，搜索左侧边界，r=mid-1，最后循环终止l==r+1，也不会遗漏*/

2.寻找最后一个满足条件的值

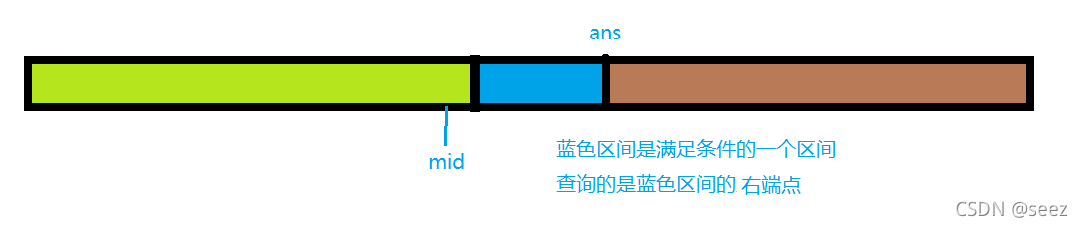
int right_bound(int x)
{
	int l = 0, r = n;
	/*while(l<r)	循环终止 l==r  循环区间[l,r)*/
	while (l < r)
	{
		int mid = l + r >> 1;
		if (a[mid] < x)		//x在右边
			l = mid + 1;	//去区间[mid+1,r)寻找
		else if (a[mid] > x)	//x在左边
			r = mid;		//去区间[l,mid)寻找
		else if (a[mid] == x)	//找到了x不是立即返回，而是去右边继续寻找
			l = mid + 1;
	}
	if (l == 0)return -1;
	return a[l - 1] == x ? l - 1 : -1;
	/*这里使用l-1，是因为找到x后搜索右侧边界，l=mid+1，可能会错过一个唯一的x
	所以这里使用l-1，同时l-1也不会越界，不需要越界检测*/
	l = 0, r = n - 1;
	//while(l<=r)	循环终止l==r+1，循环区间[l,r)
	while (l <= r)
	{
		int mid = l + r >> 1;
		if (a[mid] < x)	//x在右边
			l = mid + 1;	//去区间[mid+1,r]寻找
		else if (a[mid] > x)
			r = mid - 1;	//去区间[l,mid-1]寻找
		else if (a[mid] == x)	//继续寻找右侧端点
			l = mid + 1;	//去区间[mid+1,r]寻找
	}
	//循环终止条件为l==r+1，所以只要r不越界，那么r的值就是x的右侧边界，不需要l-1
	if (r < 0 || a[l] != x)
		return -1;
	return r;
}

y总的记忆法

int acwing(int x)
{
	//搜索左侧边界
	//[l,r]分为[l,mid],[mid+1,r]
	//[l,mid]保证了不漏

	int l = 0, r = n - 1;
	while (l < r) {
			int mid = (l + r) / 2;
			if (a[mid]>=x)	//x在左边，去左边寻找左侧边界 
				r = mid; 
			else l = mid + 1;
		}
		return l;
	
	//搜索右侧边界
	//[l,r]分为[l,mid-1][mid,r]
	//[mid,r]保证了不漏
		l = 0, r = n - 1;    
    //如果这里r=n，就会发生错误，因为mid是上取整的，那么l的取值会取到n，发生错误
	while (l < r)
	{
		int mid = (l + r + 1) >> 1;		//写了l=mid，mid就+1
		if (a[mid] <= x) l = mid;
		else r = mid - 1;
	}
	return l;
	//p.s.mid = (l + r + 1) / 2这里，+1是因为除法下取整，
	//在r = l + 1时更新l = mid时会出现l = mid = l的死循环。+1则相当于上取整，解决了这个隐患。
}
//写成l=mid mid=(l+r+1)/2
//写成l=mid+1 mid=(l+r)/2

/*
如果搜索右侧边界，不想上取整且想r=n
int right_bound(int x)
{
    int l = 0, r = n ;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (x < a[mid])
            r = mid;
        else if (x == a[mid])
            l = mid+1;      //相等的时候去右边寻找
        else if (x > a[mid])
            l = mid+1;      //去[mid+1,r)区间寻找
    }//由于去[mid+1,r)寻找，所有应该l-1
    return a[l-1] == x ? l-1 : -1;
}
*/