DRL笔记

最新推荐文章于 2025-05-17 17:49:36 发布

qiu_xiao_ying

最新推荐文章于 2025-05-17 17:49:36 发布

阅读量216

点赞数 1

文章标签：概率论机器学习自动驾驶

本文链接：https://blog.youkuaiyun.com/qiu_xiao_ying/article/details/120688671

版权

本文详细介绍了强化学习（RL）的难点和方法，重点探讨了策略梯度（policy-based approach）的三大步骤，包括神经网络作为行为者、函数优劣度量以及选取最佳函数。还讲解了PPO（策略梯度的进阶版）的概念，如on-policy与off-policy的区别。此外，文章还涉及了值基方法（value-based approach）和actor-critic方法，如Q-learning和A2C算法，讨论了连续动作问题及解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

十四.Reinforement learning

一.概述

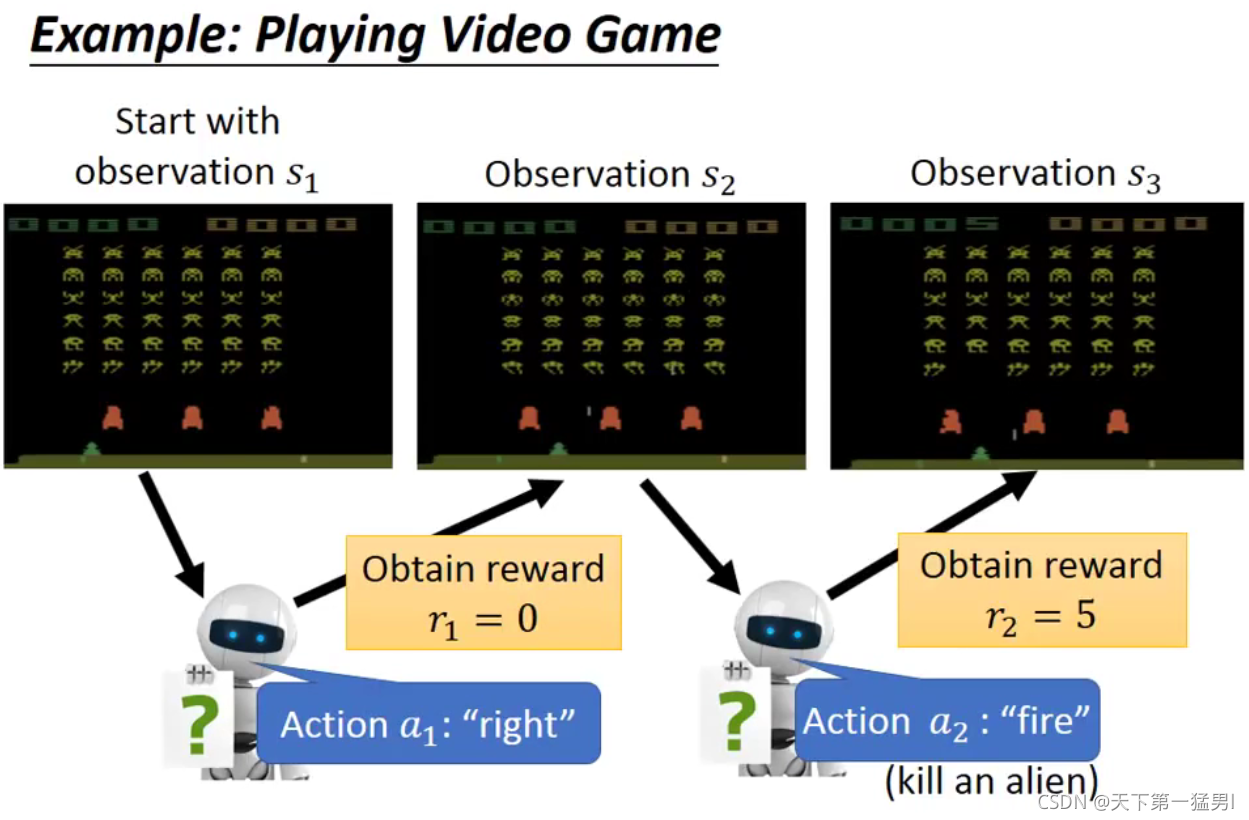
在这里插入图片描述

1.RL存在的困难

延迟奖励：虽然“向左”、“向右”移动无法得到奖励，但是有助于获得更大的奖励；
agent采取的行为会影响它看到的东西，要会探索这个世界；

2.方法

policy-based approach(learning an actor)
value-based approach(learning a critic)
actor+critic (A3C)

二.policy-based approach

1.梗概

在这里插入图片描述

2. 3大步骤

2.1 step1：neural network as actor

在这里插入图片描述
输入：observation；输出：action的分布

2.2 step2：goodness of a function

假设让actor(定义为： $\pi_\theta(s)$ )玩一场游戏(episode)从开始到结束有这样一个轨迹(trajectory)：
$\tau=\{ s_1,a_1,r_1,s_2,a_2,r_2,\dots,s_T,a_T,r_T\}$ ;
$R_\theta=\sum_{t=1}^{T}r_t$ ;
由于actor和游戏具有随机性，故 $R_\theta$ 是一个随机变量，故转而求它的期望值( $\bar{R}_\theta$ )的最大值;
期望： $\bar{R}_\theta=\sum_{\tau}R(\tau)p(\tau \vert \theta)$ ;
抽样 $\{\tau^1,\tau^2,\dots,\tau^N\}$ 估计总体:
即： $\bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N}R(\tau^n)$

2.3 step3:pick the best function

1.目标函数： $\theta^*=\argmax_{\theta}\bar{R}_{\theta}$
2.梯度上升法(policy gradient)： $\theta^{new} \leftarrow \theta^{old}+\eta\triangledown \bar{R}_\theta$
3.推导过程
$\begin{aligned}\bar{R}_\theta &=\sum_{\tau}R(\tau)p(\tau \vert \theta) \\ \triangledown \bar{R}_\theta &= \sum_{\tau}R(\tau)\triangledown{p(\tau \vert \theta)} \\ & =\sum_{\tau}R(\tau)p(\tau \vert \theta)\frac{\triangledown{p(\tau \vert \theta)}}{p(\tau \vert \theta)} \\ & =\sum_{\tau}R(\tau)p(\tau \vert \theta) \triangledown{\log p(\tau \vert \theta) } \\ & \approx \frac{1}{N}\sum_{n=1}^{N}R(\tau^n)\triangledown{\log p(\tau^n \vert \theta) } \\ \tau &=\{ s_1,a_1,r_1,s_2,a_2,r_2,\dots,s_T,a_T,r_T\} \\p(\tau \vert \theta) &=p(s_1)p(a_1 \vert s_1,\theta)p(r_1,s_2 \vert s_1,a_1)p(a_2 \vert s_2,\theta)p(r_2,s_3 \vert s_2,a_2) \dots \\ &=p(s_1)\prod_{t=1}^{T}p(a_t\vert s_t,\theta)p(r_t,s_{t+1} \vert s_t,a_t) \\ \triangledown \bar{R}_\theta & \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}R(\tau^n) \triangledown \log p(a_t^n \vert s_t^n,\theta)\end{aligned}$

最低0.47元/天解锁文章