题目描述
有 NNN 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这NNN 个任务分成若干批,每一批包含连续的若干个任务。
从时刻000开始,任务被分批加工,执行第 iii 个任务所需的时间是 TiT_iTi。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 SSS 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 CiC_iCi。
请为机器规划一个分组方案,使得总费用最小。
输入格式
第一行包含整数 NNN。
第二行包含整数 SSS。
接下来N行每行有一对整数,分别为 TiT_iTi 和 CiC_iCi,表示第 iii 个任务单独完成所需的时间 TiT_iTi 及其费用系数 CiC_iCi。
输出格式
输出一个整数,表示最小总费用。
数据范围
1≤N≤50001≤N≤50001≤N≤5000,
0≤S≤500≤S≤500≤S≤50,
1≤Ti,Ci≤1001≤T_i,C_i≤1001≤Ti,Ci≤100
输入样例
5
1
1 3
3 2
4 3
2 3
1 4
输出样例
153
算法思想(动态规划)
根据题目描述,可以将任务划分成若干批,每一批包含连续的若干个任务,且在每批任务开始前,机器需要 SSS 的启动时间。分析输入样例,可以将任务做如下划分:
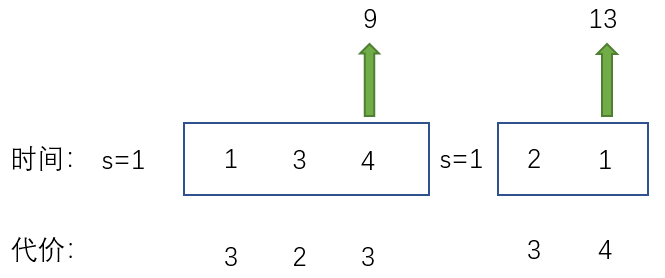
此时总费用=(3+2+3)×9+(3+4)×13=72+91=163=(3 + 2 + 3) \times 9 + (3 + 4) \times 13=72+91=163=(3+2+3)×9+(3+4)×13=72+91=163
也可以将任务做如下划分:
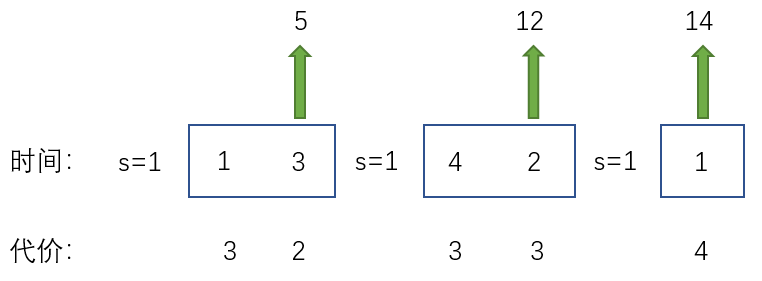
此时总费用=(3+2)×5+(4+2)×12+4×14=25+72+56=153=(3 + 2) \times 5 + (4 + 2) \times 12 + 4\times14=25+72+56=153=(3+2)×5+(4+2)×12+4×14=25+72+56=153,此时总费用最小。
从上述分析可以看出,这是一个典型线性DP求最小值问题。
状态表示
f[i]表示处理完前i个任务,所有方案的最小值
状态计算
不妨设j为前一批的最后一个任务,那么要计算f[i]可以分为下面几部分:
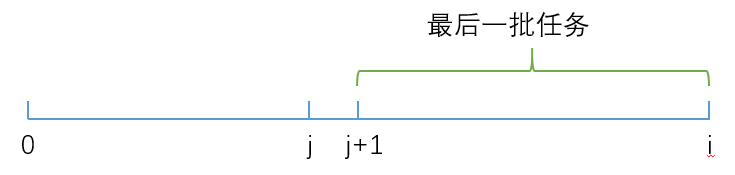
- 处理完前
j个任务的最小总代价f[j] - 完成最后一批任务(j+1∼ij + 1\sim ij+1∼i),需要花费SumTi×(SumCi−SumCj)Sum_{T_i}\times(Sum_{C_i}-Sum_{C_j})SumTi×(SumCi−SumCj)
- 其中SumTiSum_{T_i}SumTi表示第
i个任务完成的时刻,即TiT_iTi的前缀和;SumCiSum_{C_i}SumCi表示前i个任务的代价和,即CiC_iCi的前缀和
- 其中SumTiSum_{T_i}SumTi表示第
- 每一批任务的开始都会增加一个启动时间SSS,这会导致后面所有任务的完成时刻都增加SSS,所以还需要在当前阶段累加对后面所有任务带来的额外影响,即S×(SumCn−SumCj)S\times (Sum_{C_n}-Sum_{C_j})S×(SumCn−SumCj)
因此,状态转移方程可以表示为:
f[i]=min{f[j]+SumTi×(SumCi−SumCj)+S×(SumCn−SumCj)},0≤j<if[i]= min\{f[j] + Sum_{T_i}\times(Sum_{C_i}-Sum_{C_j})+S\times (Sum_{C_n}-Sum_{C_j})\}, 0\le j \lt if[i]=min{f[j]+SumTi×(SumCi−SumCj)+S×(SumCn−SumCj)},0≤j<i
时间复杂度
状态数:nnn
状态计算时间复杂度:O(n)O(n)O(n)
总的时间复杂度为:O(n2)=O(25,000,000)O(n^2) = O(25,000,000)O(n2)=O(25,000,000)
代码实现
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 5010;
LL sumt[N], sumc[N];
LL f[N];
int main()
{
int n, s;
cin >> n >> s;
for(int i = 1; i <= n; i ++)
{
cin >> sumt[i] >> sumc[i];
sumt[i] += sumt[i - 1], sumc[i] += sumc[i - 1]; //前缀和
}
//求最小值,要将数组初始化为无穷大
memset(f, 0x3f, sizeof f);
f[0] = 0; //初始状态
for(int i = 1; i <= n; i ++)
for(int j = 0; j < i; j ++)
f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));
cout << f[n] << endl;
return 0;
}

























 571
571

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










