Leetcode每日一题 539. 最小时间差

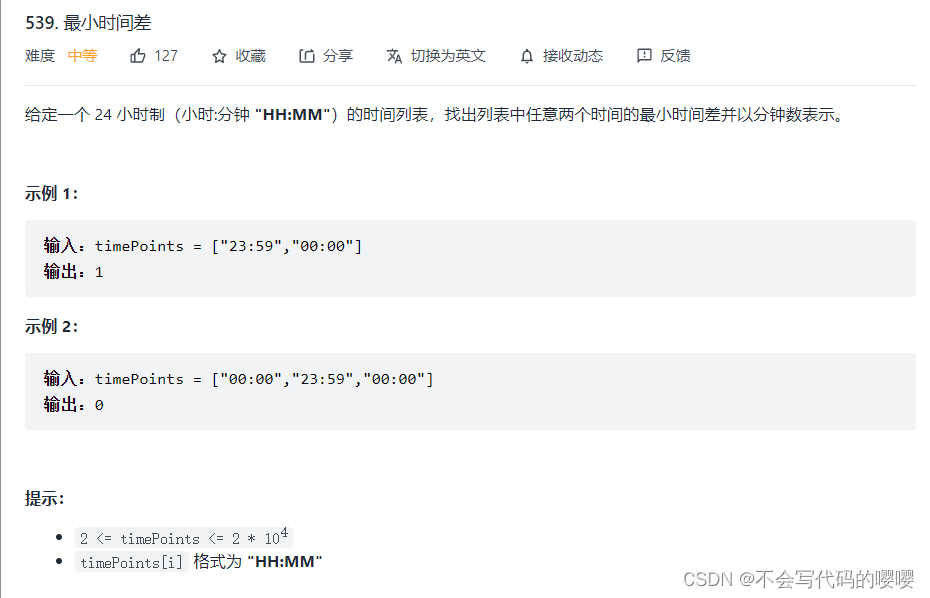
问题描述

思路分析及代码实现

方法一 模拟排序

根据题意，涉及到了一个零点的偏角问题，因此某一时间在第二天的夹角或许比当天的夹角小，所以可以在换算每一个时间时再额外把时间+1440并一起记录，这样就可以把所有的情况都考虑到，然后排序，遍历每一组相邻差找出最小值

class Solution:
    def findMinDifference(self, timePoints: List[str]) -> int:
        n = len(timePoints) * 2
        nums = [0] * n
        ids = 0
        for time in timePoints:
            nums[ids] = int(time[:2])*60 + int(time[-2:])
            nums[ids+1] = int(time[:2])*60 + int(time[-2:]) + 24*60
            ids += 2
        nums.sort()
        return min(nums[i+1]-nums[i] for i in range(n-1))

方法二 鸽巢原理

根据题意，最多有24*60=1440个时间，因此当数量超过1440时，一定存在两个相同的时间,因此可以在方法一开始加一个1440范围的判断

class Solution:
    def findMinDifference(self, timePoints: List[str]) -> int:
        m = len(timePoints)
        if m > 1440:
            return 0
        n = len(timePoints) * 2
        nums = [0] * n
        ids = 0
        for time in timePoints:
            nums[ids] = int(time[:2])*60 + int(time[-2:])
            nums[ids+1] = int(time[:2])*60 + int(time[-2:]) + 24*60
            ids += 2
        nums.sort()
        return min(nums[i+1]-nums[i] for i in range(n-1))

解释一下鸽巢原理

鸽巢原理又叫抽屉原理或狄利克雷原理，鸽巢原理的简单形式：如果n+1个物体被放进n个盒子里，那么至少有一个盒子包含两个或更多的物体