李宏毅机器学习入门学习笔记（四） Classification：Probabilistic Generative Model

最新推荐文章于 2022-12-12 12:02:13 发布

DataScience

最新推荐文章于 2022-12-12 12:02:13 发布

阅读量802

点赞数

分类专栏： Machine Learning 《李宏毅机器学习》读书笔记文章标签：李宏毅机器学习 ML 分类 Classification

本文链接：https://blog.youkuaiyun.com/q370835062/article/details/88191042

版权

本文介绍了机器学习中的分类概念，通过神奇宝贝属性预测为例，对比了回归模型与概率模型的差异。重点讲解了概率模型的实现原理，包括盒抽球概率模型、高斯分布和最大似然估计，以及如何利用这些理论进行分类模型的建立和优化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

背景

分类概念

在这里插入图片描述
分类要找一个 $f u n c t i o n$ 函数，输入对象 $x$ 特征，输出是该对象属于 $n$ 个类别中是属于哪一个。

例子1：比如信用评分【二分类问题】
- 输入：收入，储蓄，行业，年龄，金融史…
- 输出：是否拒绝拒绝贷款
例子2：比如医疗诊断【多分类问题】
- 输入：当前症状，年龄，性别，医疗史…
- 输出：患了哪种疾病
例子3：比如手写文字辨识【多分类问题】
- 输入：手写的文字
- 输出：约9353个汉字中输入哪一个

个人总结：我接触到的分类问题目前还是相对较少。在多分类问题上，如果特征复杂，类别又多，对机器的计算性能要求也相对较高。

神奇宝贝的属性（水、电、草）预测

这里再次使用《神奇宝贝》作为例子讲解。如下图，首先认识一下神奇宝贝中的属性：
在这里插入图片描述
神奇宝贝有很多的属性，比如电，火，水。要做的就是一个分类的问题：需要找到一个 $f u n c t i o n$ ，

输入：一只神奇宝贝的特征（整体强度，生命值，攻击力，防御力，特殊攻击力，特殊防御力，速度等）
输出：属于哪一种类型的神奇宝贝

首先将神奇宝贝数值化：以比卡丘为例

Total：整体强度，大概的表述神奇宝贝有多强，比如皮卡丘是320
HP：生命值，比如皮卡丘35
Attack：攻击力，比如皮卡丘55
Defense：防御力，比如皮卡丘40
SP Atk：特殊攻击力，比如皮卡丘50
SP Def：特殊防御力，比如皮卡丘50
Speed：速度，比如皮卡丘90

所以一只《神奇宝贝》可以用一个向量来表示，上述7个数字组成的向量。

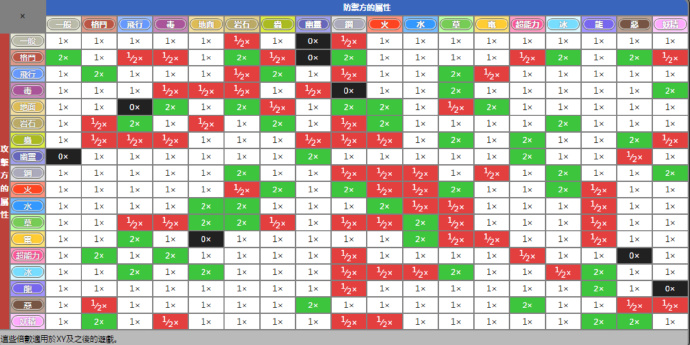
因为没有玩过《神奇宝贝》，我猜测在PK厂可以大概知道一只神奇宝贝的特征，但是不知道属于属性。因为在战斗的时候会有属性相克，下面给了张表，只需要知道，战斗的时候遇到对面神奇宝贝的特征，己方不知道属性的情况会吃亏，所以需要预测它的属性。
在这里插入图片描述

回归模型 vs 概率模型

我们收集当前神奇宝贝的特征数据和属性数据，例如：皮卡丘 $(x^1,\hat{y}^1)$ 电属性；杰尼龟 $(x^2,\hat{y}^2)$ 水属性；···；妙蛙草 $(x^3,\hat{y}^3)$ 草属性
在这里插入图片描述

回归模型

假设还不了解怎么做，但之前已经学过了 $r e g r e s s i o n$ 。就把分类当作回归硬解。
举一个二分类的例子，假设输入神奇宝贝的特征 $x$ ，判断属于类别1或者类别2，把这个当作回归问题。

类别1：相当于target是 $1$ 。
类别2：相当于target是 $- 1$ 。

然后训练模型：因为是个数值，如果数值比较接近 $1$ ，就当作类别1，如果数值接近 $- 1$ ，就当做类别2。这样做遇到什么问题？

在这里插入图片描述

左图：绿色是分界线，红色叉叉就是 Class2 的类别，蓝色圈圈就是 Class1 的类别。
右图：紫色是分界线，红色叉叉就是 Class2 的类别，蓝色圈圈就是 Class1 的类别。训练集添加有很多的距离远大于1的数据后，分界线从绿色偏移到紫色

这样用回归的方式硬训练可能会得到紫色的这条。直观上就是将绿色的线偏移一点到紫色的时候，就能让右下角的那部分的值不是那么大了。但实际是绿色的才是比较好的，用回归硬训练并不会得到好结果。此时可以得出用回归的方式定义，对于分类问题来说是不适用的。

还有另外一个问题：比如多分类，类别1当作target1，类别2当作target2，类别3当作target3…如果这样做的话，就会认为类别2和类别3是比较接近的，认为它们是有某种关系的；认为类别1和类别2也是有某种关系的，比较接近的。但是实际上这种关系不存在，它们之间并不存在某种特殊的关系。这样是没有办法得到好的结果。