7-3 找零钱***（天梯赛）

收银员现有 n 张面值分别为 v​1​​,v​2​​,…,v​n​​ 的纸币。若找零金额为 m，则一共有多少种找零方法？

注：0<n≤1000，0<v​1​​,v​2​​,…,v​n​​≤10000，0<m≤10000
输入格式

n v​1​​,v​2​​,...,v​n​​ m

输出格式

若有解，则输出全部找零方案，每输出一种 若无解，则输出“None”

输入样例1

6
3 1 4 3 2 7
9

输出样例1

3 1 3 2
3 4 2
4 3 2
2 7

输入样例2

5
5 3 4 6 7
2

输出样例2

None
思路：深度搜索每一种组合方案，用一个book数组存储答案，输出满足的方案。
如样例：
路径 选取数 当前凑出的零钱sum1 要求数 9
第一步： 选3 3
第二步： 选1 4
第三步： 选4 8
第四步： 选3 11（大于要求，返回上一步 选下一个数）
第四步： 选2 10（大于要求，返回上一步 选下一个数）
第四步： 选7 15（大于要求，返回上一步 选下一个数）
第三步： 选3 7
第四步： 选2 9 满足条件
以此类推依次往后搜索
树形结构如下

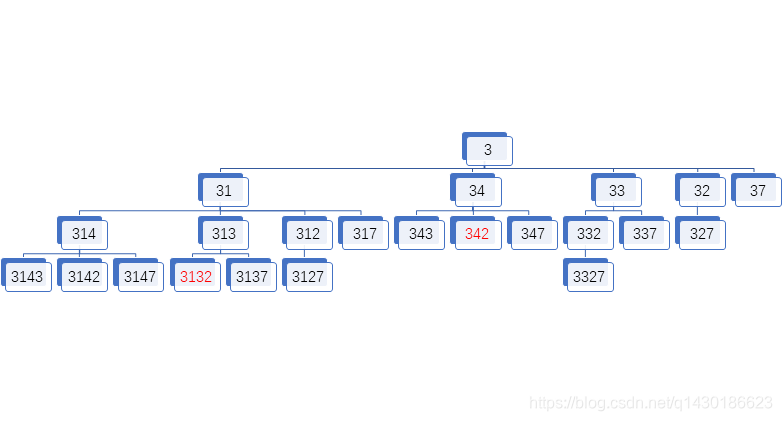
以先选3为例构建一棵树，如果后面还有数未被选并且当前凑出的零钱小于9，继续往下添加子节点；如果大于等于9，便不向下延伸，即剪枝的思想。

#include <iostream>
using namespace std;
#include <stdio.h>
#include