堆排序（headSort）

堆排序（headSort）

定义

按照惯例我们先来点入门的知识点，这样方便大家理解后面的知识点。
按照百科的说法，堆排序是指利用堆积树这种数据结构所设计的一种排序算法，但对于没有接触这个算法的人来说，会误以为是需要将数组转化为一种树型结构再进行排序，但其实并不是如此，堆排序只是利用树的性质，并利用数组的特点快速定位指定索引位置。
举个例子：
数组 【1，2，3，4，5，6】，长度为len=6
我们可以把它看作是一棵完全二叉树的存储结构

那么对于任何非叶子结点（1，2，3）来说，它们的左、右子结点为 i*2 , i*2+1 (如果存在)；
最后一个非叶子结点就是len/2；
比如结点i=1的左孩子结点为 1*2=2， 右孩子结点为 1*2+1=3 。最后一个非叶子结点为 6/2=3；

• 注意这里是下标从1开始，如果下标从0开始，即【0,1,2,3,4,5】，那么非叶子结点的左右子结点为 *i*2+1 , i*2+2 ;最后一个非叶子结点则为len/2-1;

堆排序

理解完上面这些，再来学习堆排序就相对简单多了。
我先讲一下堆排序思路：

1、构造最大堆（最小堆）

首先，构造最大堆（或最小堆），最大堆要求父结点不小于其左右子结点（最小堆就是父结点不大于其左右子结点），举个例子吧，看下图，图1是最大堆，图2是最小堆

如何构造最大堆？从最后一个非叶子结点开始，从右往左，从下往上遍历结点，每一个结点都与其左右子结点相比较（如果存在），如果父结点的值小于其子结点的值 ，则将父结点与子结点的位置进行调换。遍历完之后，数组中的最大值就会被移动到堆顶。

2、把堆顶元素与最后一个元素互换位置，对前len-1个元素重新进行构造最大堆。

把堆顶元素与最后一个元素互换位置，对剩余前len-1个元素重新进行构造最大堆，重新此过程直到只剩下最后一个元素，这时候数组就已经排序完成。

举个粟子吧

数组【16，7，3，20，17，8】，len=6
先把它看成一棵完全二叉树

接下来我们进行构造最大堆，首先从最后一个非叶子结点（3）开始，3比8小，将3跟8交换位置
—–》
然后我们再看倒数第二个非叶子结点（7），7 < 16 < 20 ，7跟20交换位置
—–》
第2层的非叶子结点已经遍历完，接下来再往上找非叶子结点，看16，16 < 20 ，所以16跟20交换位置
——》
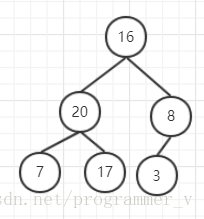这样最大值已经移动到了堆顶，将堆顶元素与最后一个元素交换位置，重新构造前len-1位元素（即【3，16，8，7，17】，len=5）的最大堆，再与第len位元素交换位置。

例子是参考这位老哥的：https://www.cnblogs.com/0zcl/p/6737944.html

最后给上用java实现的代码

package 算法题;/**
 * Created by VLoye on 2018/7/26.
 */

/**
 * @author VLoye
 * @ClassName HeapSort
 * @Description
 * @Date 11:50  2018/7/26
 * @Version 1.0
 **/
public class HeapSort {

    private static void heapSort(int[] arr) {
        int len = arr.length ;
        //len/2-1 即最后一个有孩子的结点
       makeHeap(arr,len);
        len--;
        while (len >=0){
            swap(arr,0,len);    //将堆顶元素与尾节点交换后，长度减1，尾元素最大
            makeHeap(arr,len--);    //再次对堆进行调整
        }
    }
    //构造堆  自下往上
    public static void makeHeap(int[] arr,int len){
        for(int i = len/2 - 1; i >=0; i --){ //堆构造,自下往上
            heapAndjust(arr,i,len);
        }
    }
    //被makeHeap调用
    public static  void heapAndjust(int[] arr,int i,int len){
        int left,right,j ;
        while((left = 2*i+1) < len){    //判断当前父节点有无左节点（即有无孩子节点，left为左节点）
            if((right=left+1) >= len)
                right = left;
            j = left;   //j"指针指向左节点"
            if(j < len && arr[left] < arr[right])    //右节点大于左节点
                j ++;     //当前把"指针"指向右节点
            if(arr[i] < arr[j])    //将父节点与孩子节点交换（如果上面if为真，则arr[j]为右节点，如果为假arr[j]则为左节点）
                swap(arr,i,j);
            else         //说明比孩子节点都大，直接跳出循环语句
                break;
            i = j;
        }
    }

    public static  void swap(int[] arr,int i,int len){
        int temp = arr[i];
        arr[i] = arr[len];
        arr[len] = temp;
    }

    public static void main(String[] args) {
        int array[] = {20,50,20,40,70,10,80,30,60,90};
        int array2[] ={16,7,3,20,17,8};
        System.out.println("排序之前：");
        for(int element : array2){
            System.out.print(element+" ");
        }
        heapSort(array2);
        System.out.println("\n排序之后：");
        for(int element : array2){
            System.out.print(element+" ");
        }
    }
}

其实理解了也不是很难，就是 重复构造最大堆，交换堆顶跟最后一位元素的位置，直到堆只有一个元素。