深度学习之卷积神经网络（一）-优快云博客

视觉处理三大任务：图像分类、目标检测、图像分割

上游：提取特征，CNN

下游：分类、目标、分割等，具体的业务

1. 概述

卷积神经网络是深度学习在计算机视觉领域的突破性成果。在计算机视觉领域, 往往我们输入的图像都很大，使用全连接网络的话，计算的代价较高。另外图像也很难保留原有的特征，导致图像处理的准确率不高。

卷积神经网络（Convolutional Neural Network，CNN）是一种专门用于处理具有网格状结构数据的深度学习模型。最初，CNN主要应用于计算机视觉任务，但它的成功启发了在其他领域应用，如自然语言处理等。

卷积神经网络（Convolutional Neural Network）是含有卷积层的神经网络. 卷积层的作用就是用来自动学习、提取图像的特征。

CNN网络主要有三部分构成：卷积层、池化层和全连接层构成，其中卷积层负责提取图像中的局部特征；池化层用来大幅降低运算量并特征增强；全连接层类似神经网络的部分，用来输出想要的结果。

1.1 使用场景

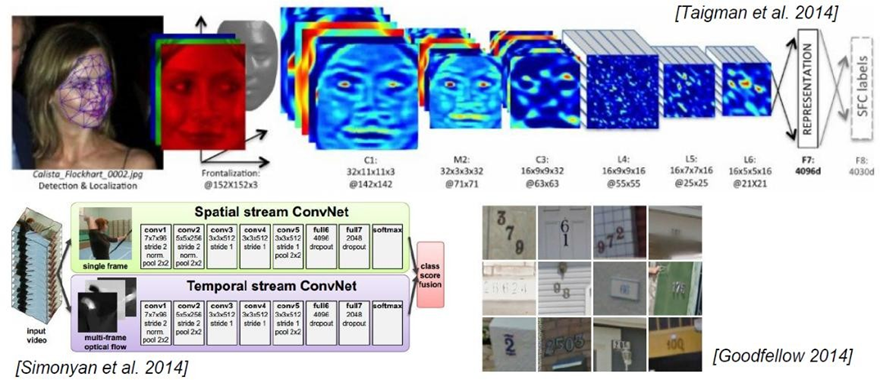
1.2 与传统网络的区别

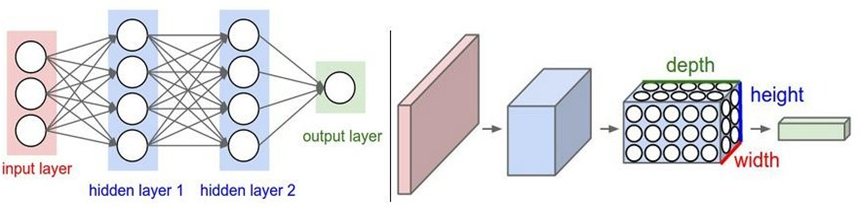
1.3 全连接的局限性

全连接神经网络并不太适合处理图像数据....

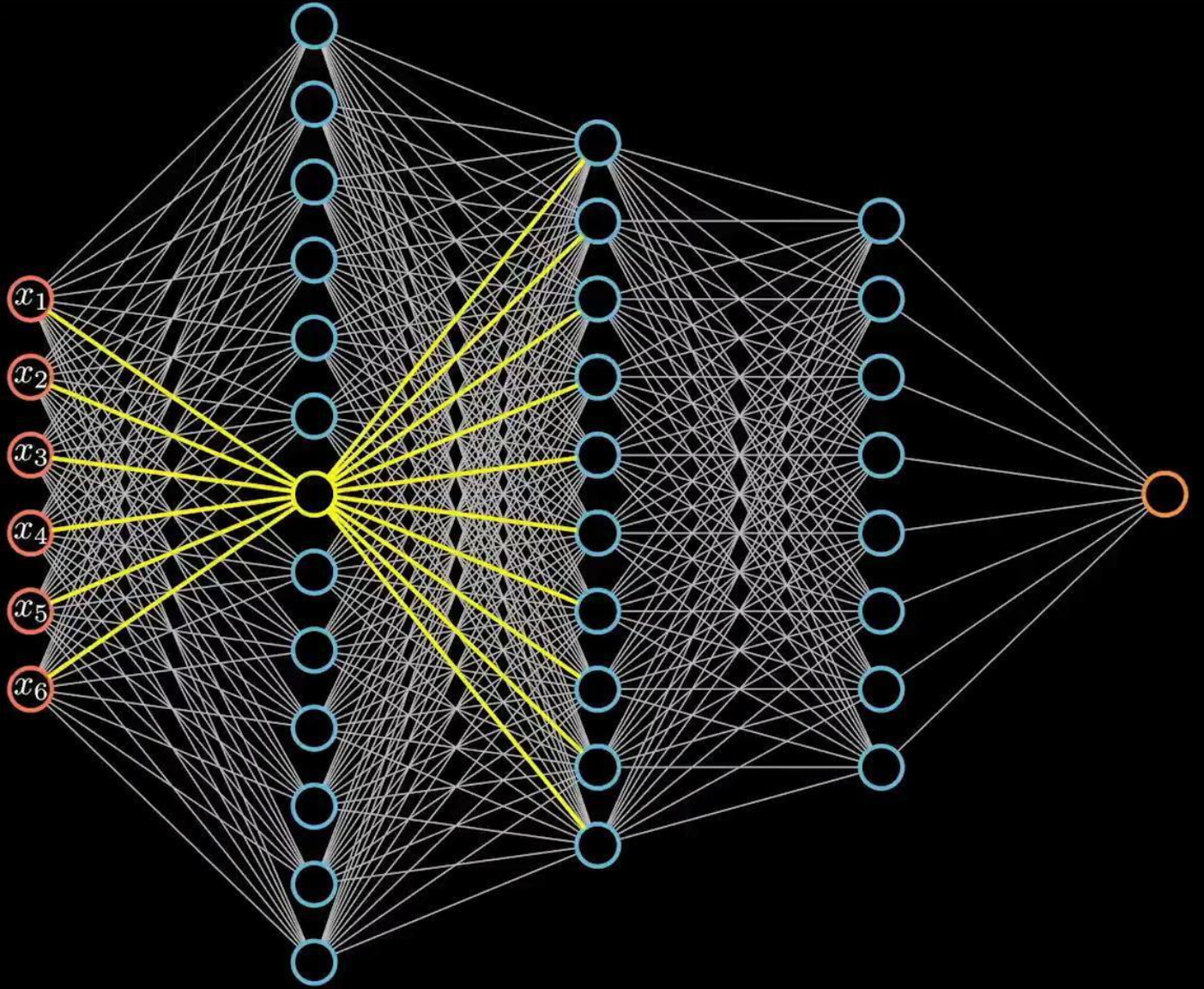
1.3.1 参数量巨大

$$
y = x \times W^T + b
$$

全连接结构计算量非常大，假设我们有1000×1000的输入，如果隐藏层也是1000×1000大小的神经元，由于神经元和图像每一个像素连接，则参数量会达到惊人的1000×1000×1000×1000，仅仅一层网络就已经有10^{12}个参数。

1.3.2 表达能力太有限

全连接神经网络的角色只是一个分类器，如果将整个图片直接输入网络，不仅参数量大，也没有利用好图片中像素的空间特性，增加了学习难度，降低了学习效果。

1.4 卷积思想

卷：从左往右，从上往下

积：乘积，求和

1.4.1 概念

Convolution，输入信息与卷积核(滤波器,Filter)的乘积。

1.4.2 局部连接

局部连接可以更好地利用图像中的结构信息，空间距离越相近的像素其相互影响越大。
根据局部特征完成目标的可辨识性。

1.4.3 权重共享

图像从一个局部区域学习到的信息应用到其他区域。
减少参数，降低学习难度。

2. 卷积层

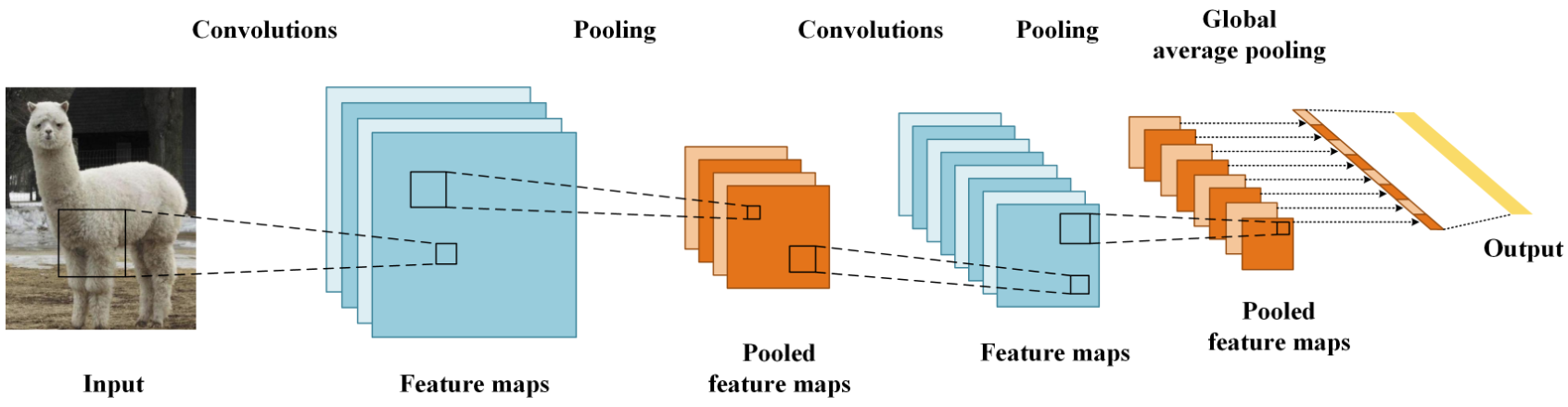
接下来，我们开始学习卷积核的计算过程, 即: 卷积核是如何提取特征的。

2.1 卷积核

卷积核是卷积运算过程中必不可少的一个“工具”，在卷积神经网络中，卷积核是非常重要的，它们被用来提取图像中的特征。

卷积核其实是一个小矩阵，在定义时需要考虑以下几方面的内容：

卷积核的个数：卷积核（过滤器）的个数决定了其输出特征矩阵的通道数。
卷积核的值：卷积核的值是初始化好的，后续进行更新。
卷积核的大小：常见的卷积核有1×1、3×3、5×5等，一般都是奇数 × 奇数。

下图就是一个3×3的卷积核：

2.2 卷积计算

2.2.1 卷积计算过程

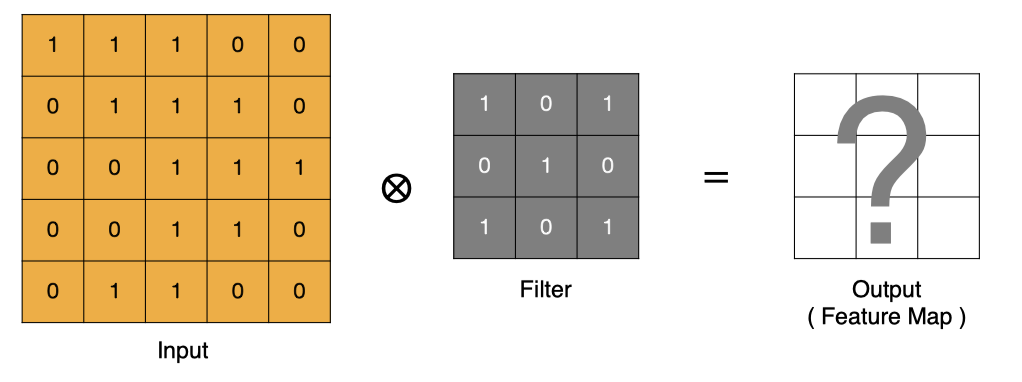
卷积的过程是将卷积核在图像上进行滑动计算，每次滑动到一个新的位置时，卷积核和图像进行点对点的计算，并将其求和得到一个新的值，然后将这个新的值加入到特征图中，最终得到一个新的特征图。

input 表示输入的图像
filter 表示卷积核, 也叫做滤波器
input 经过 filter 的得到输出为最右侧的图像，该图叫做特征图

那么, 它是如何进行计算的呢？卷积运算本质上就是在滤波器和输入数据的局部区域间做点积。

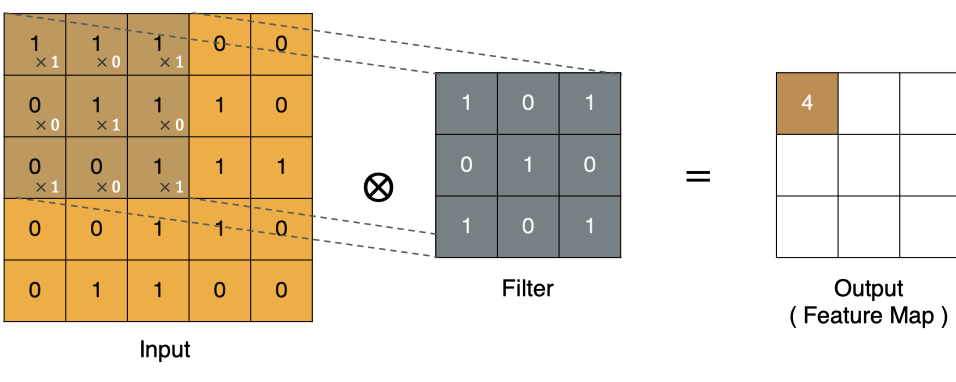
左上角的点计算方法：

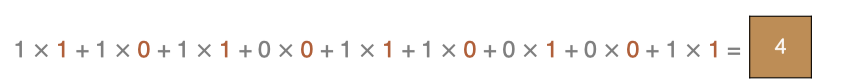
按照上面的计算方法可以得到最终的特征图为:

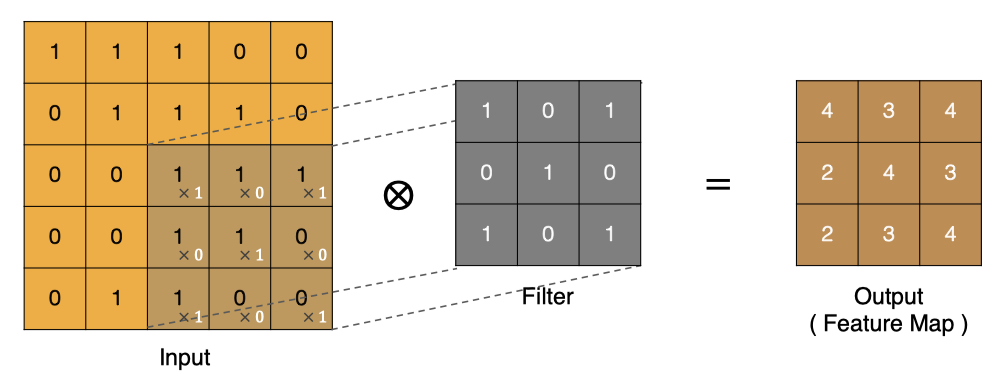
卷积的重要性在于它可以将图像中的特征与卷积核进行卷积操作，从而提取出图像中的特征。

可以通过不断调整卷积核的大小、卷积核的值和卷积操作的步长，可以提取出不同尺度和位置的特征。

 # 面向对象的模块化编程
 from matplotlib import pyplot as plt
 import os
 import torch
 import torch.nn as nn
 
 
 def test001():
     current_path = os.path.dirname(__file__)
     img_path = os.path.join(current_path, "data", "彩色.png")
     # 转换为相对路径
     img_path = os.path.relpath(img_path)
 
     # 使用plt读取图片
     img = plt.imread(img_path)
     print(img.shape)
     # 转换为张量：HWC  ---> CHW  ---> NCHW  链式调用
     img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)
     # 创建卷积核  (501, 500, 4)
     conv = nn.Conv2d(
         in_channels=4,  # 输入通道
         out_channels=32,  # 输出通道
         kernel_size=(5, 3),  # 卷积核大小
         stride=1,  # 步长
         padding=0,  # 填充
         bias=True
     )
     # 使用卷积核对图像进行卷积操作  [9999]  [[[[]]]]
     out = conv(img)
     
     # 输出128个特征图
     conv2 = nn.Conv2d(
         in_channels=32,  # 输入通道
         out_channels=128,  # 输出通道
         kernel_size=(5, 5),  # 卷积核大小
         stride=1,  # 步长
         padding=0,  # 填充
         bias=True
     )
     out = conv2(out)
     print(out)
     # 把图像显示出来
     print(out.shape)
     plt.imshow(out[0][10].detach().numpy(), cmap='gray')
     plt.show()
 
 
 # 作为主模块执行
 if __name__ == "__main__":
     test001()

2.2.2 卷积计算底层实现

并不是水平和垂直方向的循环。

下图是卷积的基本运算方式：

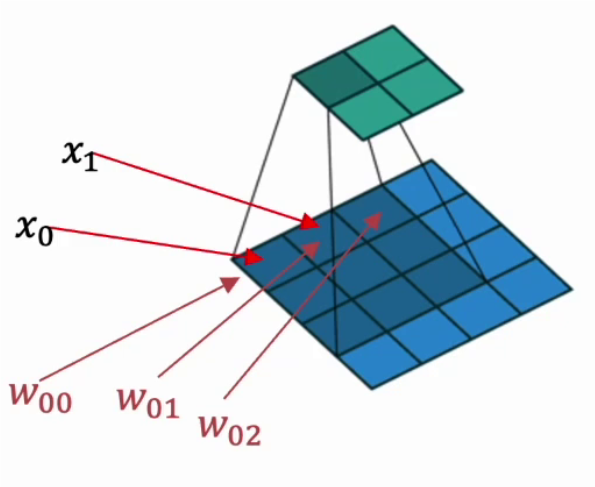
卷积真正的计算过程如下图：

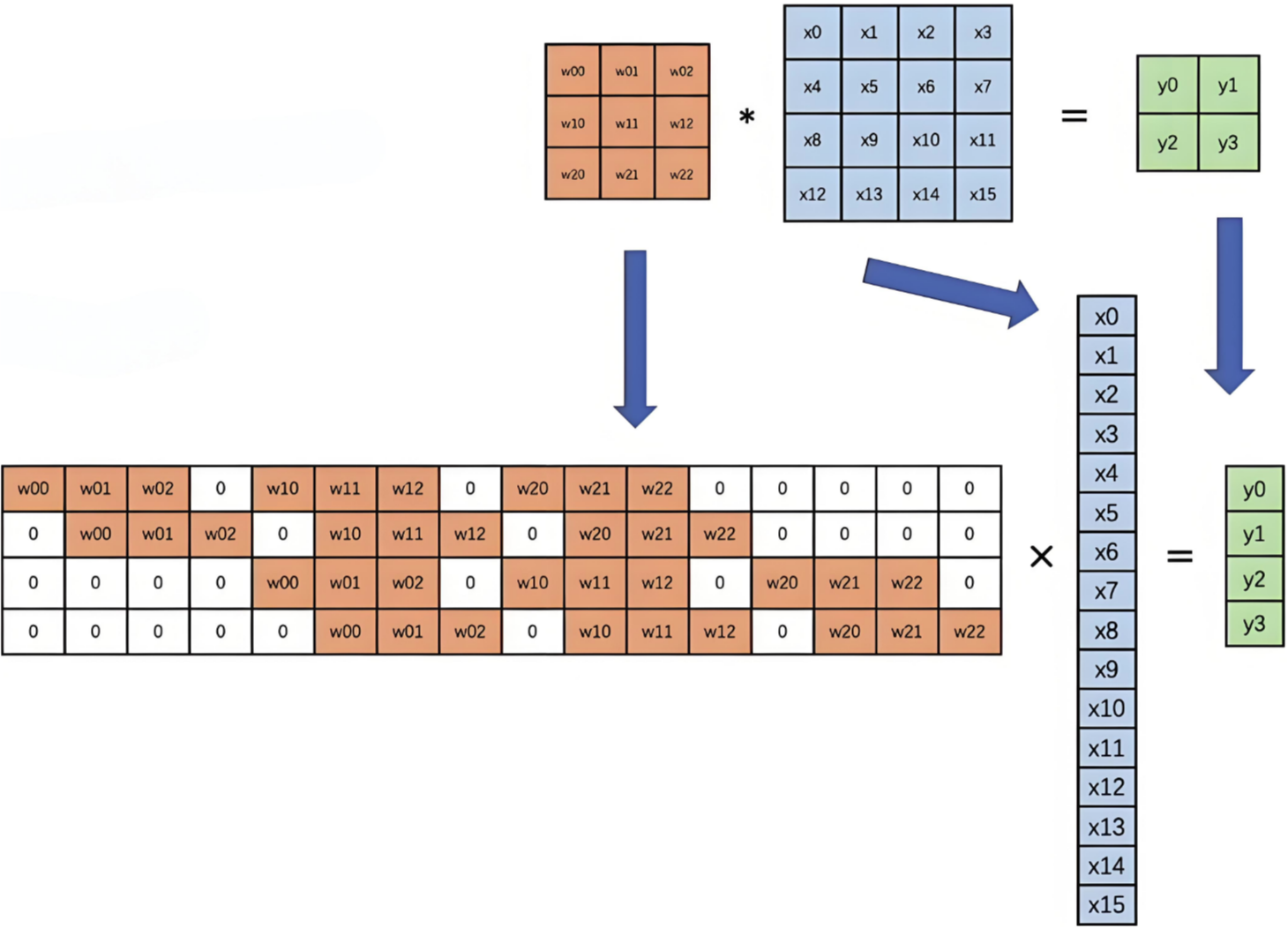
2.3 边缘填充

Padding

通过上面的卷积计算，我们发现最终的特征图比原始图像要小，如果想要保持图像大小不变, 可在原图周围添加padding来实现。

更重要的，边缘填充还更好的保护了图像边缘数据的特征。

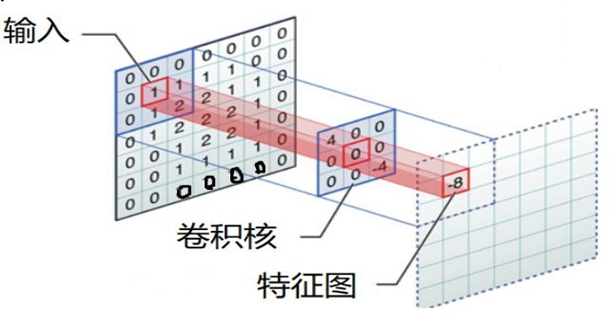
2.4 步长Stride

按照步长为1来移动卷积核，计算特征图如下所示：

如果我们把 Stride 增大为2，也是可以提取特征图的，如下图所示：

stride太小：重复计算较多，计算量大，训练效率降低； stride太大：会造成信息遗漏，无法有效提炼数据背后的特征；

2.5 多通道卷积计算

首先我们需要认识下通道，做到颗粒度对齐~

2.5.1 数字图像的标识

我们知道图像在计算机眼中是一个矩阵

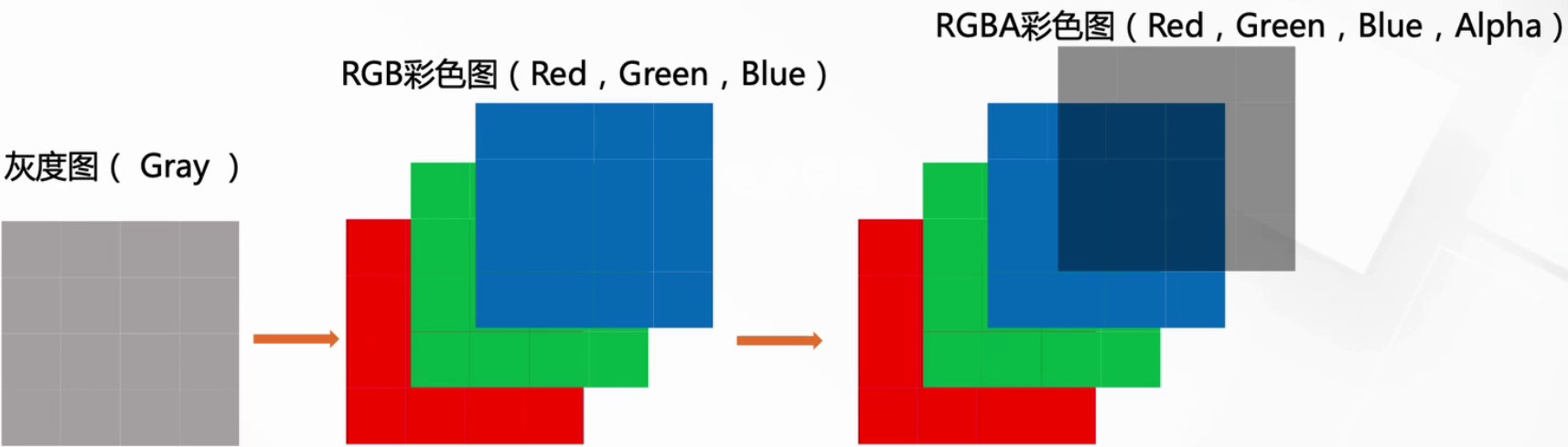
通道越多，可以表达的特征就越丰富~

2.5.2 具体计算实现

实际中的图像都是多个通道组成的，我们怎么计算卷积呢？

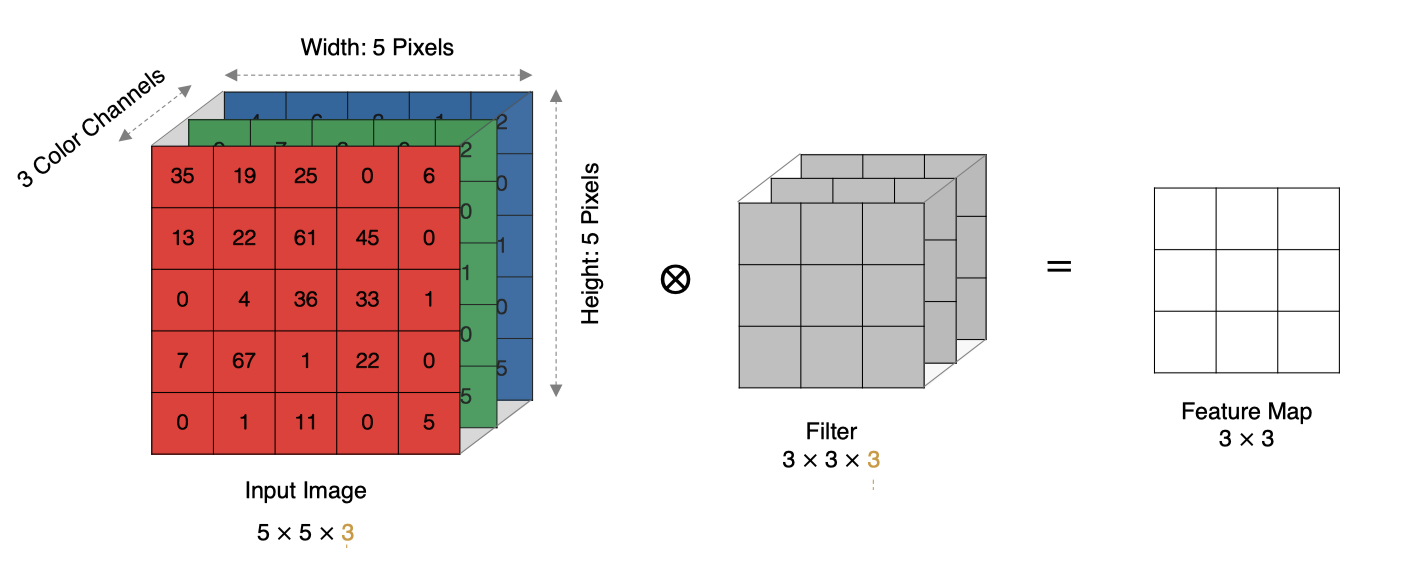
计算方法如下：

当输入有多个通道(Channel), 例如RGB三通道, 此时要求卷积核需要有相同的通道数。
卷积核通道与对应的输入图像通道进行卷积。
将每个通道的卷积结果按位相加得到最终的特征图。

如下图所示:

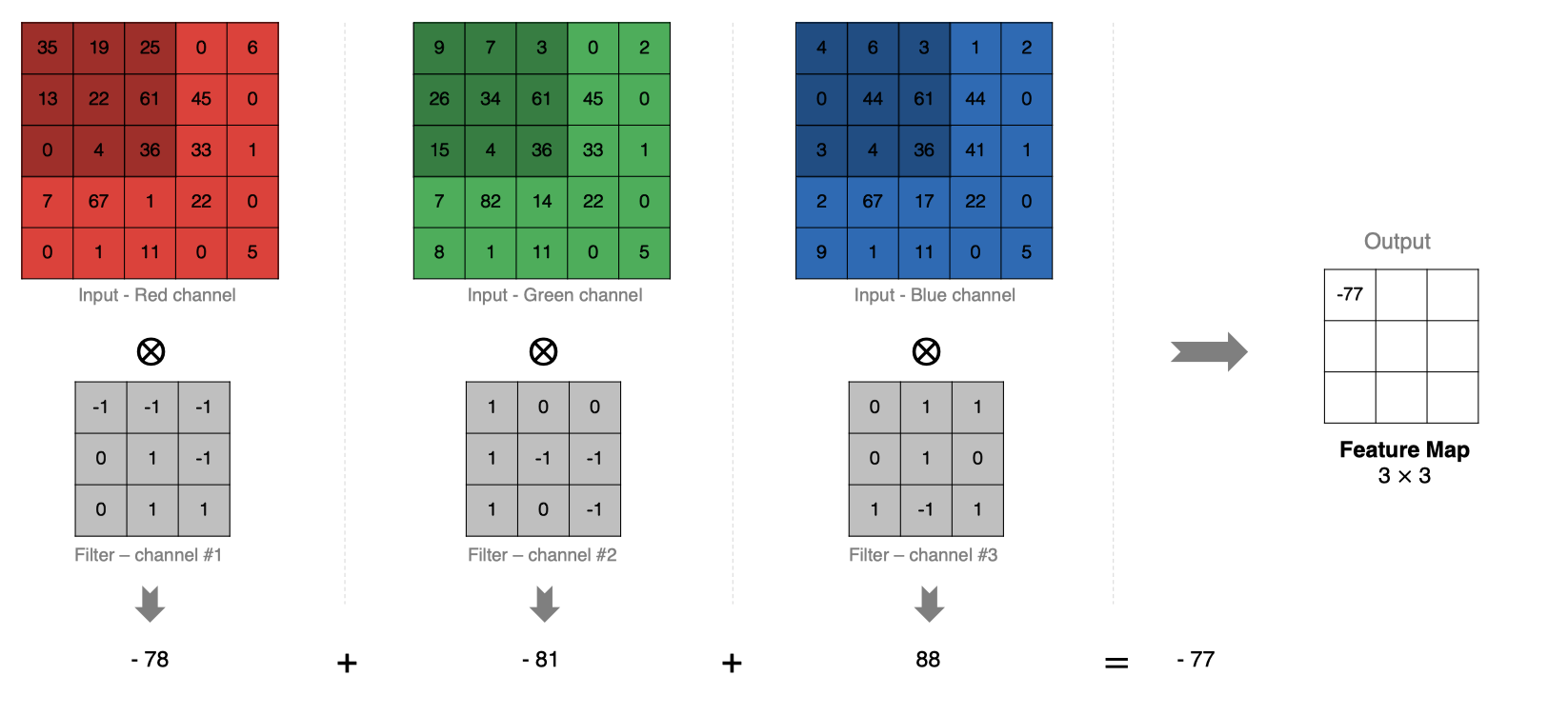
2.6 多卷积核卷积计算

实际对图像进行特征提取时, 我们需要使用多个卷积核进行特征提取。这个多个卷积核可以理解为从不同到的视角、不同的角度对图像特征进行提取。

那么, 当使用多个卷积核时, 应该怎么进行特征提取呢?

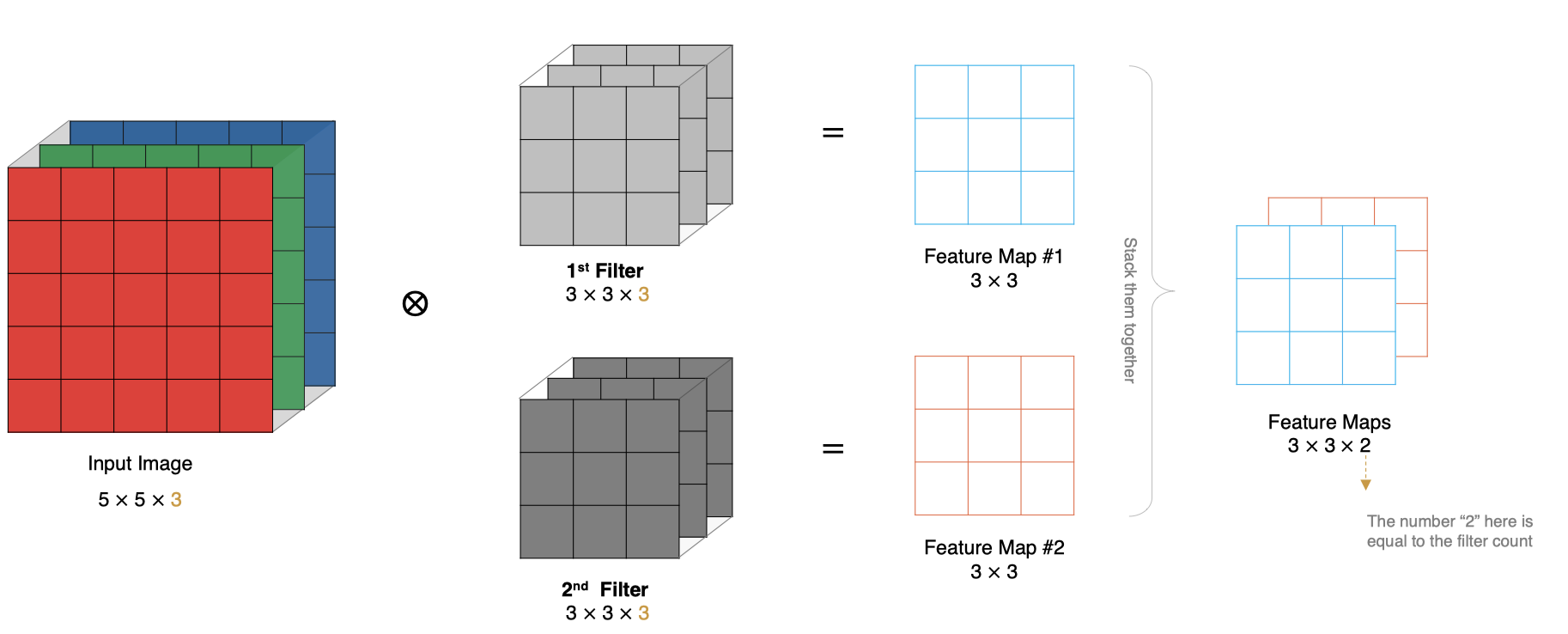
2.7 特征图大小

输出特征图的大小与以下参数息息相关:

size: 卷积核/过滤器大小，一般会选择为奇数，比如有 1×1, 3×3， 5×5
Padding: 零填充的方式
Stride: 步长

那计算方法如下图所示:

输入图像大小: W x W
卷积核大小: F x F
Stride: S
Padding: P
输出图像大小: N x N

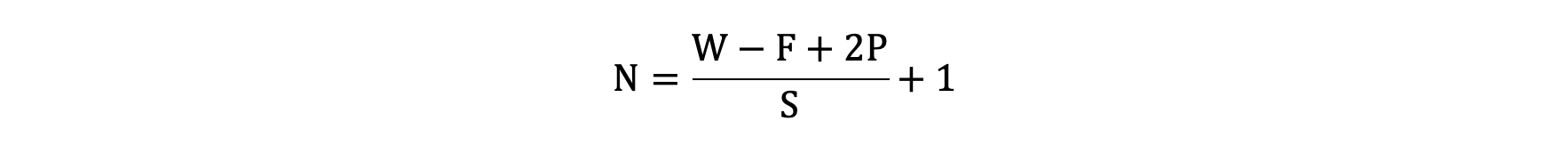
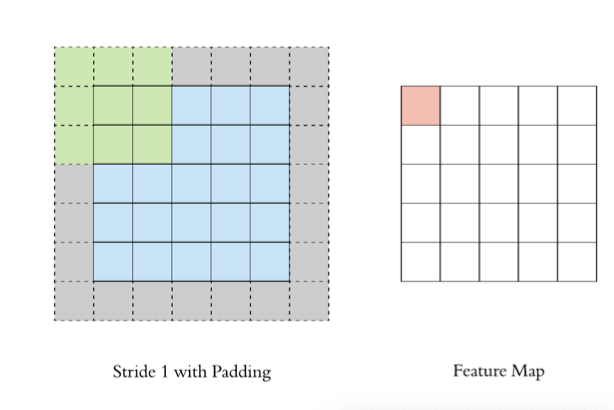
以下图为例:

图像大小: 5 x 5
卷积核大小: 3 x 3
Stride: 1
Padding: 1
(5 - 3 + 2) / 1 + 1 = 5, 即得到的特征图大小为: 5 x 5

2.8 只卷一次？

2.9 卷积参数共享

数据是 32×32×3 的图像，用 10 个 5×5 的filter来进行卷积操作，所需的权重参数有多少个呢？

5×5×3 = 75，表示每个卷积核只需要75个参数。
10个不同的卷积核，就需要10*75 = 750个卷积核参数。
如果还考虑偏置参数b，最终需要 750+10=760 个参数。

$$
全连接参数量： 10 * 28 * 28 *(32 * 32 * 3 + 1)
$$

2.10 局部特征提取

通过卷积操作，CNN具有局部感知性，能够捕捉输入数据的局部特征，这在处理图像等具有空间结构的数据时非常有用。

2.11 PyTorch卷积层 API

test01 函数使用一个多通道卷积核进行特征提取, test02 函数使用 3 个多通道卷积核进行特征提取:

 import torch
 import torch.nn as nn
 import matplotlib.pyplot as plt
 import os
 
 
 def showimg(img):
     plt.imshow(img)
     # 隐藏刻度
     plt.axis("off")
     plt.show()
 
 
 def test001():
     dir = os.path.dirname(__file__)
     img = plt.imread(os.path.join(dir, "彩色.png"))
     # 创建卷积核
     # in_channels：输入数据的通道数
     # out_channels：输出特征图数，和filter数一直
     conv = nn.Conv2d(in_channels=4, out_channels=1, kernel_size=3, stride=1, padding=1)
     # 注意：卷积层对输入的数据有形状要求 [batch, channel, height, width]
     # 需要进行形状转换  H, W, C -> C, H, W
     img = torch.tensor(img, dtype=torch.float).permute(2, 0, 1)
     print(img.shape)
     # 接着变形：CHW -> BCHW
     newimg = img.unsqueeze(0)
     print(newimg.shape)
     # 送入卷积核运算一下
     newimg = conv(newimg)
     print(newimg.shape)
 
     # 蒋NCHW->HWC
     newimg = newimg.squeeze(0).permute(1, 2, 0)
     showimg(newimg.detach().numpy())
 
 
 # 多卷积核
 def test002():
     dir = os.path.dirname(__file__)
     img = plt.imread(os.path.join(dir, "彩色.png"))
     # 定义一个多特征图输出的卷积核
     conv = nn.Conv2d(in_channels=4, out_channels=3, kernel_size=3, stride=1, padding=1)
 
     # 图形要进行变形处理
     img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)
     
     # 使用卷积核对图片进行卷积计算
     outimg = conv(img)
     print(outimg.shape)
     # 把图形形状转换回来以方便显示
     outimg = outimg.squeeze(0).permute(1, 2, 0)
     print(outimg.shape)
     # showimg(outimg)
     # 显示这些特征图
     for idx in range(outimg.shape[2]):
         showimg(outimg[:, :, idx].squeeze(-1).detach())
 
 
 if __name__ == "__main__":
     test002()

效果：