注意力机制

目录

一、基本概念

二、实现过程

三、注意力机制公式

---

一、基本概念

QKV术语

假设你去图书馆查资料。你想要写一篇关于“恐龙灭绝”的报告。

比如你心里想的是：“我想知道小行星撞击对恐龙灭绝的影响”。这就是你要查询的问题（Query），是你当前的需求。

图书馆里收集了很多书记，并记录了所有书籍的目录、索引、书名（Key）。假设有一本书的书名是《恐龙时代》，另一本是《地球地质演变》，还有一本是《宇宙天体学》。这些 Key 是书籍内容的“标签”或“摘要”，用于快速匹配你的问题。

每本书中记录了书籍内部完整的、详细的内容（Value）。它是你最终想要获取的信息本身。

所以，注意力机制通过引入查询向量（Query）、键向量（Key）、值向量（Value）概念来实现序列中各元素之间的信息交互和依赖建模。

• Q：Query

  表示当前查询者的位置，用来发出问题。

• K：Key

  表示被查询者的身份，是所有位置给出的“介绍信”或“标签”。

• V：Value

  表示被查询者实际信息。

二、实现过程

以图书馆查资料为例。

Query (Q)：你的需求 = “小行星撞击对恐龙灭绝的影响”。这是一个抽象的“问题向量”。

Keys (K)：三本书的标题/索引（用于匹配）。

• k₁ = “宇宙天体学” （Key for Book 1）

• k₂ = “恐龙时代” （Key for Book 2）

• k₃ = “地球地质演变” （Key for Book 3）

Values (V)：三本书的详细内容（信息的真正载体）。

• v₁ = 《宇宙天体学》书中所有关于小行星、撞击、地质层铱异常等的内容。

• v₂ = 《恐龙时代》书中所有关于恐龙化石断代、灭绝时间线、生态系统崩溃等的内容。

• v₃ = 《地球地质演变》书中所有关于气候变迁、火山活动、地层年代等的内容。

第1步：评分（Score） - “匹配问题与索引”

动作：你将你的问题（Query）与图书馆的每个索引（Key）进行比对，看它们有多相关。

数学计算：计算Query q 与每个Key kᵢ 的相似度分数。最常用的是点积（Dot Product），其几何意义是衡量两个向量的方向是否相近（可以理解为点积是未标准化的余弦相似度）。

那么如何计算相似度分数呢？

主要有三种方法：KNN，余弦相似度，点积

• s(q, k₁) = q · k₁ （问题 vs “宇宙天体学”）

• s(q, k₂) = q · k₂ （问题 vs “恐龙时代”）

• s(q, k₃) = q · k₃ （问题 vs “地球地质演变”）

结果：假设计算结果的分数为：score₁ = 12, score₂ = 6, score₃ = 2

显然，“宇宙天体学”(k₁)与你的问题最相关，得分最高；“恐龙时代”(k₂)次之；“地球地质演变”(k₃)最不相关，得分最低。

第2步：缩放与归一化（Scale & Softmax） - “计算注意力权重”

• 动作：你根据匹配度，决定在最终的报告中，每本书的内容应该占多大比例。

• 数学计算：

  1. 缩放（Scale）：将上一步每个分数除以一个缩放因子（√d_k，d_k是Key向量的维度）。这是为了在向量维度很高时，防止点积分数过大导致后续Softmax函数的梯度太小。

     • 假设 √d_k = 4，则缩放后分数：12/4=3, 6/4=1.5, 2/4=0.5

  2. 归一化（Softmax）：将缩放后的分数输入Softmax函数。Softmax将所有分数转换为一个概率分布：所有值在0到1之间，且总和为1。这个结果就是注意力权重（αᵢ）。

     • α₁ = e³ / (e³ + e¹·⁵ + e⁰·⁵) ≈ 0.84

     • α₂ = e¹·⁵ / (e³ + e¹·⁵ + e⁰·⁵) ≈ 0.12

     • α₃ = e⁰·⁵ / (e³ + e¹·⁵ + e⁰·⁵) ≈ 0.04

• 结果：你决定，在最终答案中，84% 的信息源自《宇宙天体学》，12% 源自《恐龙时代》，4% 源自《地球地质演变》。注意力权重 [0.84, 0.12, 0.04] 就是你大脑分配的“注意力”。

说明：为什么要缩放？（了解）

Softmax会放大差异，使得概率最大的类别的输出值更接近1，而其他类别更接近0。

比如 [1, 2] 放大10倍 -> [10, 20]

$$
Softmax([10, 20]) = [\frac{e^{10}}{e^{10}+e^{20}}, \frac{e^{20}}{e^{10}+e^{20}}]
$$

e^20 相比于 e^10 是一个巨大的数，因此计算结果无限接近于 [0, 1]。

Softmax输出会收敛到一个极端尖锐的、近乎one-hot的分布。

如果对Softmax求导：

$$
\begin{aligned} &\text{设 }p_i=\mathrm{Softmax}(z_i)\text{,则对于 }z_i\text{ 的导数为:} \\ &\bullet\text{ 当 }i=j\text{ 时:} \\ &&&\frac{\partial p_i}{\partial z_i}=\frac{e^{z_i}(\Sigma_{j=1}^ne^{z_j})-e^{z_i}e^{z_i}}{(\Sigma_{j=1}^ne^{z_j})^2}=p_i(1-p_i) \\ & \bullet\text{ 当 }i\neq j\text{ 时}: \\ &&&\frac{\partial p_i}{\partial z_j}=\frac{0(\Sigma_{j=1}^ne^{z_j})-e^{z_i}e^{z_j}}{(\Sigma_{j=1}^ne^{z_j})^2} =-p_{i}p_{j} \end{aligned}
$$

对于得分20的那个位置，pi=1，它的梯度是：p_i(1-p_i)=1*(1-1)=0。

对于得分10的那个位置，pi=0，它的梯度是：p_i(1-p_i)=0*(1-0)=0。

第3步：加权求和（Weighted Sum） - “合成最终报告”

• 动作：你不是简单地复制粘贴《宇宙天体学》整本书，而是从三本书中分别抽取与问题相关的段落和句子，然后按照84%、12%、4%的比例组合、润色，形成一份连贯、全面的最终报告。

• 数学计算：将第2步得到的每个权重 αᵢ 与其对应的完整内容 vᵢ（Value）相乘，然后将所有结果相加，得到最终的输出向量。

  • V'= (α₁ * v₁) + (α₂ * v₂) + (α₃ * v₃)

  • V'= (0.84 * “小行星、铱异常...”) + (0.12 * “化石断代、生态崩溃...”) + (0.04 * “气候变迁、火山...”)

• 比喻结果：你得到了一份全新的、定制化的报告。这份报告：

  • 核心（84%）来自《宇宙天体学》的详细科学解释。

  • 用《恐龙时代》（12%）的证据进行了支撑和年代定位。

  • 轻微提及（4%）了《地球地质演变》中其他可能理论作为对比。

  • 它不是任何一本现成的书，而是根据你的特定问题从所有来源中动态提取、融合而成的精华。

综上所述，经过计算后就得到了一个新的 V'，这个新的 V' 就包含了，哪些更重要，哪些不重要的信息在里面，然后用 V' 代替 V

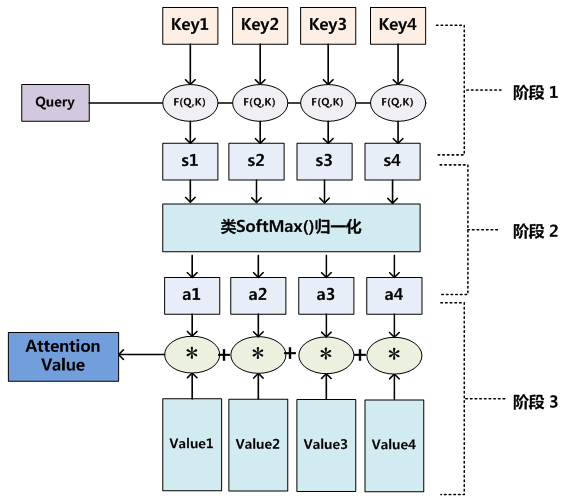
总结：

1. 评分 score(q, kᵢ) = q · kᵢ ：用你的问题去匹配所有书的索引 ，得到一组原始相关性分数

2. 归一化 αᵢ = softmax(score / √d_k) ：根据匹配度决定每本书的参考比例 ，得到注意力权重（一个概率分布）

3. 求和 Output = Σ (αᵢ * vᵢ) ： 按比例从每本书中抽取内容并组合成文， 生成最终的、上下文相关的输出

核心思想：注意力机制的输出永远是一个混合体（Mixture）。它不是简单地选择某一个Value，而是所有Value的加权和。

三、注意力机制公式

$$
\text{Attention} = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) \times V
$$

详细计算步骤

1. 计算注意力分数

分数矩阵 = QK^T

这一步计算查询和键之间的相似度。

1. 缩放（Scaling）

缩放后的分数 = \frac{QK^T}{\sqrt{d_k}}

除以\sqrt{d_k}是为了防止点积结果过大，导致softmax函数的梯度太小。

1. 应用Softmax

注意力权重 = softmax(\frac{QK^T}{\sqrt{d_k}})

将分数转换为概率分布，所有权重之和为1。

1. 加权求和

输出 = 注意力权重 × V

用注意力权重对值向量进行加权求和。

矩阵维度说明

假设：

• 输入序列长度：n

• 查询/键维度：d_k

• 值维度：d_v

• 批次大小：b

则：

• Q: (b,n,d_k)

• K: (b,n,d_k)

• K^T: (b,d_k,n)

• QK^T: (b,n,n)

• V: (b,n,d_v)

• 输出: (b,n,d_v)

如何理解呢？

• Q（查询）：每个 token 的 “查询向量” 集合，比如 “一个批次 b 条文本，每条 n 个 token，每个 token 用 d_q 维向量表示”，这里Q查询向量的子词（token）的维度通常与d_k相同，也就是就是 (b, n, d_k)；
• K（键）：每个 token 的 “键向量” 集合，和 Q 维度完全一致 —— 因为后续要做 “Q 与 K 的点积”（同维度向量才能算点积），所以必须都是 (b, n, d_k)。

---

技术分享是一个相互学习的过程。关于本文的主题，如果你有不同的见解、发现了文中的错误，或者有任何不清楚的地方，都请毫不犹豫地在评论区留言。我很期待能和大家一起讨论，共同补充更多细节。