昨天我们认识了Torch的核心——Tensor,然后学习了它的概念、特点和类型。接着,介绍了三种创建Tensor的方法,以及如何查看和改变Tensor的属性、设备和类型。学会了如何在PyTorch(Tensor)和Numpy这两个生态之间进行数据转换。初步介绍了Tensor的一些基本运算操作,为后续更复杂的模型搭建打下了坚实的基础,今天我们继续torch的学习。
目录
六、Tensor 常见操作
5. 形状操作
在 PyTorch 中,张量的形状操作至关重要,它允许灵活调整张量的维度和结构,以满足不同的计算需求。
5.1 reshape
reshape 方法用于改变张量的形状,但需确保转换后的形状与原始形状的元素数量一致。
import torch
def test001():
data1 = torch.randint(0, 10, (4, 3))
print(data1)
# 1. 使用 reshape 改变形状
data2 = data1.reshape(2, 2, 3)
print(data2)
# 2. 使用 -1 表示自动计算维度
data3 = data1.reshape(2, -1)
print(data3)
if __name__ == "__main__":
test001()-
data1的元素个数为 4×3=12 -
data2的元素个数也应为 12,即 2×2×3=12 -
data3中-1表示自动计算,此处等价于data1.reshape(2, 6)
5.2 view
view 方法也用于形状变换,但具有特定的内存连续性要求。
5.2.1 内存连续性
张量的内存布局决定了元素在内存中的存储顺序。多维张量通常按最后一个维度优先的顺序存储(C 顺序)。若张量的内存布局与形状完全匹配且未被转置、索引等操作打乱,则该张量是连续的。
import torch
def test001():
tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
print("正常情况下的张量:", tensor.is_contiguous())
# 对张量进行转置操作
tensor = tensor.t()
print("转置后的张量:", tensor.is_contiguous())
print(tensor)
# 尝试使用 view 进行变形操作
try:
tensor = tensor.view(2, -1)
print(tensor)
except RuntimeError as e:
print("错误信息:", e)
if __name__ == "__main__":
test001()转置后的张量内存不连续,而 view() 要求内存连续,因此会报错。解决方案是使用 reshape() 或先调用 contiguous()。
5.2.2 与 reshape 的比较
-
view:高效,但要求张量内存连续 -
reshape:更灵活,可能涉及内存复制
5.2.3 view 变形操作
import torch
def test002():
tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 将 2x3 张量转换为 3x2
reshaped_tensor = tensor.view(3, 2)
print(reshaped_tensor)
# 自动推断一个维度
reshaped_tensor = tensor.view(-1, 2)
print(reshaped_tensor)
if __name__ == "__main__":
test002()5.3 transpose
transpose 用于交换张量的两个维度,返回原张量的视图。
torch.transpose(input, dim0, dim1)
参数说明:
-
input:输入张量 -
dim0:要交换的第一个维度 -
dim1:要交换的第二个维度
import torch
def test003():
data = torch.randint(0, 10, (3, 4, 5))
print(data, data.shape)
# 使用 transpose 进行形状变换
transpose_data = torch.transpose(data, 0, 1)
# 或者:transpose_data = data.transpose(0, 1)
print(transpose_data, transpose_data.shape)
if __name__ == "__main__":
test003()注意:
-
transpose返回新张量,原张量不变 -
转置后的张量可能是非连续的,必要时可调用
.contiguous()
5.4 permute
permute 通过重新排列张量的维度来返回新张量,不改变数据,只改变维度顺序。
torch.permute(input, dims)
参数说明:
-
input:输入张量 -
dims:新的维度顺序
import torch
def test004():
data = torch.randint(0, 10, (3, 4, 5))
print(data, data.shape)
# 使用 permute 进行多维度形状变换
permute_data = data.permute(1, 2, 0)
print(permute_data, permute_data.shape)
if __name__ == "__main__":
test004()注意:
-
维度顺序必须合法且包含所有原始维度
-
重排后的张量可能非连续,必要时需调用
.contiguous()
注意:
维度顺序必须合法:dims 中的维度顺序必须包含所有原始维度,且不能重复或遗漏。例如,对于一个形状为 (2, 3, 4) 的张量,dims=(2, 0, 1) 是合法的,但 dims=(0, 1) 或 dims=(0, 1, 2, 3) 是非法的。
与 transpose() 的对比
| 特性 | permute() | transpose() |
|---|---|---|
| 功能 | 可同时调整多个维度顺序 | 只能交换两个维度 |
| 灵活性 | 更灵活 | 较简单 |
| 使用场景 | 适用于多维张量 | 适用于简单维度交换 |
5.5 升维和降维
在网络学习中,升维和降维是常用操作。
5.5.1 squeeze 降维
torch.squeeze(input, dim=None)
参数说明:
-
input:输入张量 -
dim:可选,指定要降维的维度(若为 None,则移除所有大小为 1 的维度)
import torch
def test006():
data = torch.randint(0, 10, (1, 4, 5, 1))
print(data, data.shape)
# 进行降维操作
data1 = data.squeeze(0).squeeze(-1)
print(data1.shape)
# 移除所有大小为 1 的维度
data2 = torch.squeeze(data)
print(data2.shape)
# 尝试移除第 1 维(大小为 4,不为 1,张量保持不变)
data3 = torch.squeeze(data, dim=1)
print("尝试移除第 1 维后的形状:", data3.shape)
if __name__ == "__main__":
test006()5.5.2 unsqueeze 升维
torch.unsqueeze(input, dim)
参数说明:
-
input:输入张量 -
dim:要插入新维度的位置
import torch
def test007():
data = torch.randint(0, 10, (32, 32, 3))
print(data.shape)
# 升维操作
data = data.unsqueeze(0)
print(data.shape)
if __name__ == "__main__":
test007()6. 广播机制
广播机制允许对不同形状的张量进行计算,无需显式调整形状。它通过自动扩展较小维度的张量,使其与较大维度的张量兼容。
6.1 广播机制规则
-
从尾部维度开始对齐
-
维度大小相等或其中一个为 1 时可广播
-
缺失维度视为 1
6.2 广播案例
1D 和 2D 张量广播
import torch
def test006():
data1d = torch.tensor([1, 2, 3])
data2d = torch.tensor([[4], [2], [3]])
print(data1d.shape, data2d.shape)
# 自动进行广播
print(data1d + data2d)
if __name__ == "__main__":
test006()输出:
torch.Size([3]) torch.Size([3, 1])
tensor([[5, 6, 7],
[3, 4, 5],
[4, 5, 6]])
理解

2D 和 3D 张量广播
import torch
def test001():
# 2D 张量
a = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 3D 张量
b = torch.tensor([[[2, 3, 4]], [[5, 6, 7]]])
print(a.shape, b.shape)
# 进行运算
result = a + b
print(result, result.shape)
if __name__ == "__main__":
test001()执行结果:
torch.Size([2, 3]) torch.Size([2, 1, 3])
tensor([[[ 3, 5, 7],
[ 6, 8, 10]],
[[ 6, 8, 10],
[ 9, 11, 13]]]) torch.Size([2, 2, 3])
七、自动微分
自动微分模块torch.autograd负责自动计算张量操作的梯度,具有自动求导功能。自动微分模块是构成神经网络训练的必要模块,可以实现网络权重参数的更新,使得反向传播算法的实现变得简单而高效。
1. 基础概念
-
张量
Torch中一切皆为张量,属性requires_grad决定是否对其进行梯度计算。默认是 False,如需计算梯度则设置为True。
-
计算图:
torch.autograd通过创建一个动态计算图来跟踪张量的操作,每个张量是计算图中的一个节点,节点之间的操作构成图的边。
在 PyTorch 中,当张量的 requires_grad=True 时,PyTorch 会自动跟踪与该张量相关的所有操作,并构建计算图。每个操作都会生成一个新的张量,并记录其依赖关系。当设置为
True时,表示该张量在计算图中需要参与梯度计算,即在反向传播(Backpropagation)过程中会自动计算其梯度;当设置为False时,不会计算梯度。例如:
在上述代码中,x 和 y 是输入张量,即叶子节点,z 是中间结果,loss 是最终输出。每一步操作都会记录依赖关系:
叶子节点:即所有输入的特征
z = x * y:z 依赖于 x 和 y。
loss = z.sum():loss 依赖于 z。
这些依赖关系形成了一个动态计算图,如右图所示: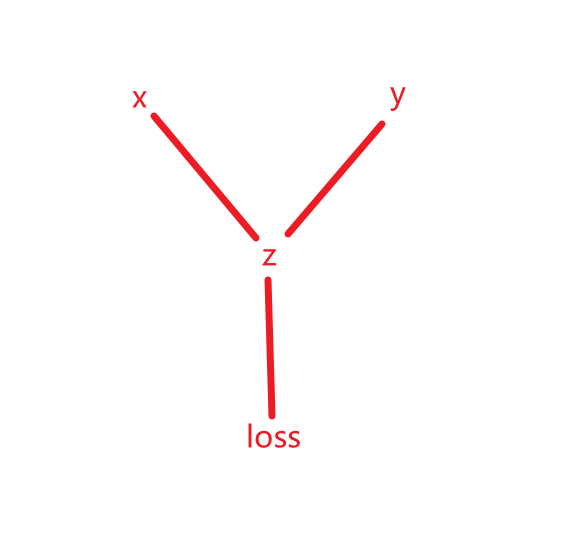
叶子节点:
在 PyTorch 的自动微分机制中,叶子节点(leaf node) 是计算图中:
-
由用户直接创建的张量,并且它的 requires_grad=True。
-
这些张量是计算图的起始点,通常作为模型参数或输入变量。
特征:
-
没有由其他张量通过操作生成。
-
如果参与了计算,其梯度会存储在 leaf_tensor.grad 中。
-
默认情况下,叶子节点的梯度不会自动清零,需要显式调用 optimizer.zero_grad() 或 x.grad.zero_() 清除。
如何判断一个张量是否是叶子节点?
通过 tensor.is_leaf 属性,可以判断一个张量是否是叶子节点。
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True) # 叶子节点 y = x ** 2 # 非叶子节点(通过计算生成) z = y.sum() print(x.is_leaf) # True print(y.is_leaf) # False print(z.is_leaf) # False
叶子节点与非叶子节点的区别
| 特性 | 叶子节点 | 非叶子节点 |
|---|---|---|
| 创建方式 | 用户直接创建的张量 | 通过其他张量的运算生成 |
| is_leaf 属性 | True | False |
| 梯度存储 | 梯度存储在 .grad 属性中 | 梯度不会存储在 .grad,只能通过反向传播传递 |
| 是否参与计算图 | 是计算图的起点 | 是计算图的中间或终点 |
| 删除条件 | 默认不会被删除 | 在反向传播后,默认被释放(除非 retain_graph=True) |
detach():张量 x 从计算图中分离出来,返回一个新的张量,与 x 共享数据,但不包含计算图(即不会追踪梯度)。
特点:
-
返回的张量是一个新的张量,与原始张量共享数据。
-
对 x.detach() 的操作不会影响原始张量的梯度计算。
-
推荐使用 detach(),因为它更安全,且在未来版本的 PyTorch 中可能会取代 data。
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True) y = x.detach() # y 是一个新张量,不追踪梯度 y += 1 # 修改 y 不会影响 x 的梯度计算 print(x) # tensor([1., 2., 3.], requires_grad=True) print(y) # tensor([2., 3., 4.])
-
反向传播
使用tensor.backward()方法执行反向传播,从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。例如:调用 loss.backward() 从输出节点 loss 开始,沿着计算图反向传播,计算每个节点的梯度。
-
梯度
计算得到的梯度通过tensor.grad访问,这些梯度用于优化模型参数,以最小化损失函数。
2. 计算梯度
使用 tensor.backward() 方法执行反向传播,计算张量梯度。
2.1 标量梯度计算
import torch
def test001():
# 创建张量(必须为浮点类型)
x = torch.tensor(1.0, requires_grad=True)
# 操作张量
y = x ** 2
# 计算梯度(反向传播)
y.backward()
# 读取梯度值
print(x.grad) # 输出: tensor(2.)
if __name__ == "__main__":
test001()2.2 向量梯度计算
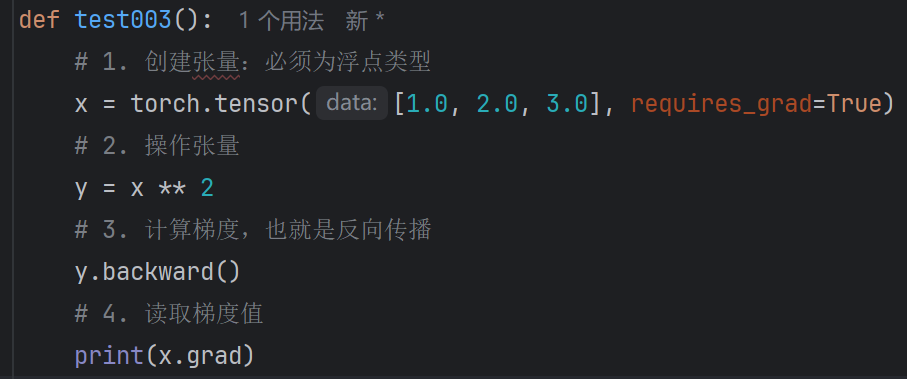
这样会错误预警:RuntimeError: grad can be implicitly created only for scalar outputs
由于 y 是一个向量,我们需要提供一个与 y 形状相同的向量作为 backward() 的参数,这个参数通常被称为 梯度张量(gradient tensor),它表示 y 中每个元素的梯度。
import torch
def test003():
# 创建张量
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
# 操作张量
y = x ** 2
# 计算梯度(需提供梯度张量)
y.backward(torch.tensor([1.0, 1.0, 1.0]))
# 读取梯度值
print(x.grad) # 输出: tensor([2., 4., 6.])
if __name__ == "__main__":
test003()或将向量转换为标量:
import torch
def test002():
# 创建张量
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
# 操作张量
y = x ** 2
# 损失函数
loss = y.mean()
# 计算梯度
loss.backward()
# 读取梯度值
print(x.grad) # 输出: tensor([0.6667, 1.3333, 2.0000])
if __name__ == "__main__":
test002()调用 loss.backward() 从输出节点 loss 开始,沿着计算图反向传播,计算每个节点的梯度。
损失函数,其中 n=3。
对于每个 ,其梯度为
。
对于每个 ,其梯度为:
所以,x.grad 的值为:
2.3 多标量梯度计算
import torch
def test003():
# 创建两个标量
x1 = torch.tensor(5.0, requires_grad=True, dtype=torch.float64)
x2 = torch.tensor(3.0, requires_grad=True, dtype=torch.float64)
# 构建运算公式
y = x1**2 + 2 * x2 + 7
# 计算梯度
y.backward()
# 读取梯度值
print(x1.grad, x2.grad) # 输出: tensor(10., dtype=torch.float64) tensor(2., dtype=torch.float64)
if __name__ == "__main__":
test003()2.4 多向量梯度计算
import torch
def test004():
# 创建两个张量
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = torch.tensor([4.0, 5.0, 6.0], requires_grad=True)
# 前向传播:计算 z = x * y
z = x * y
# 前向传播:计算 loss = z.sum()
loss = z.sum()
# 查看前向传播结果
print("z:", z) # 输出: tensor([ 4., 10., 18.], grad_fn=<MulBackward0>)
print("loss:", loss) # 输出: tensor(32., grad_fn=<SumBackward0>)
# 反向传播:计算梯度
loss.backward()
# 查看梯度
print("x.grad:", x.grad) # 输出: tensor([4., 5., 6.])
print("y.grad:", y.grad) # 输出: tensor([1., 2., 3.])
if __name__ == "__main__":
test004()3. 梯度上下文控制
梯度计算的上下文控制和设置对于管理计算图、内存消耗、以及计算效率至关重要。下面我们学习下Torch中与梯度计算相关的一些主要设置方式。
3.1 控制梯度计算
梯度计算是有性能开销的,有些时候我们只是简单的运算,并不需要梯度
import torch
def test001():
x = torch.tensor(10.5, requires_grad=True)
print(x.requires_grad) # True
# 1. 默认 y 的 requires_grad=True
y = x**2 + 2 * x + 3
print(y.requires_grad) # True
# 2. 使用 with 进行上下文管理
with torch.no_grad():
y = x**2 + 2 * x + 3
print(y.requires_grad) # False
# 3. 使用装饰器
@torch.no_grad()
def y_fn(x):
return x**2 + 2 * x + 3
y = y_fn(x)
print(y.requires_grad) # False
# 4. 全局设置(需谨慎)
torch.set_grad_enabled(False)
y = x**2 + 2 * x + 3
print(y.requires_grad) # False
if __name__ == "__main__":
test001()3.2 累计梯度
默认情况下,梯度是累加的。
import torch
def test002():
# 创建张量
x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)
# 累计梯度:每次计算都会累计梯度
for i in range(3):
y = x**2 + 2 * x + 7
z = y.mean()
z.backward()
print(x.grad)
if __name__ == "__main__":
test002()输出:
tensor([1.3333, 2.0000, 4.2000]) tensor([2.6667, 4.0000, 8.4000]) tensor([ 4.0000, 6.0000, 12.6000])
3.3 梯度清零
import torch
def test002():
# 创建张量
x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)
# 每次计算前清零梯度
for i in range(3):
y = x**2 + 2 * x + 7
z = y.mean()
# 反向传播前先对梯度进行清零
if x.grad is not None:
x.grad.zero_()
z.backward()
print(x.grad)
if __name__ == "__main__":
test002()输出:
tensor([1.3333, 2.0000, 4.2000]) tensor([1.3333, 2.0000, 4.2000]) tensor([1.3333, 2.0000, 4.2000])
3.4 案例1-求函数最小值
通过梯度下降找到函数最小值。
import torch
from matplotlib import pyplot as plt
import numpy as np
def test01():
x = np.linspace(-10, 10, 100)
y = x ** 2
plt.plot(x, y)
plt.show()
def test02():
# 初始化自变量 X
x = torch.tensor([3.0], requires_grad=True, dtype=torch.float)
# 迭代轮次
epochs = 50
# 学习率
lr = 0.1
list = []
for i in range(epochs):
# 计算函数表达式
y = x ** 2
# 梯度清零
if x.grad is not None:
x.grad.zero_()
# 反向传播
y.backward()
# 梯度下降(不需要计算梯度)
with torch.no_grad():
x -= lr * x.grad
print('epoch:', i, 'x:', x.item(), 'y:', y.item())
list.append((x.item(), y.item()))
# 散点图,观察收敛效果
x_list = [l[0] for l in list]
y_list = [l[1] for l in list]
plt.scatter(x=x_list, y=y_list)
plt.show()
if __name__ == "__main__":
test01()
test02()注意:不能直接对叶子变量进行原地更新,需使用 torch.no_grad() 或 x.data。
3.5 案例2-函数参数求解
import torch
def test02():
# 定义数据
x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)
y = torch.tensor([3, 5, 7, 9, 11], dtype=torch.float)
# 定义模型参数 a 和 b,并初始化
a = torch.tensor([1], dtype=torch.float, requires_grad=True)
b = torch.tensor([1], dtype=torch.float, requires_grad=True)
# 学习率
lr = 0.01 # 注意:学习率过大会导致发散
# 迭代轮次
epochs = 500
for epoch in range(epochs):
# 前向传播:计算预测值 y_pred
y_pred = a * x + b
# 定义损失函数
loss = ((y_pred - y) ** 2).mean()
if a.grad is not None and b.grad is not None:
a.grad.zero_()
b.grad.zero_()
# 反向传播:计算梯度
loss.backward()
# 梯度下降
with torch.no_grad():
a -= lr * a.grad
b -= lr * b.grad
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')
print(f'a: {a.item()}, b: {b.item()}')
if __name__ == '__main__':
test02()通过适当的学习率和迭代次数,参数 a 和 b 会收敛到真实值附近。
以上就是 PyTorch 张量形状操作与自动微分的详细内容,这些基础知识对于理解和构建神经网络模型至关重要。
技术分享是一个相互学习的过程。关于本文的主题,如果你有不同的见解、发现了文中的错误,或者有任何不清楚的地方,都请毫不犹豫地在评论区留言。我很期待能和大家一起讨论,共同补充更多细节。





















 1315
1315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








