目录
一、神经网络
我们要学习的深度学习(Deep Learning)是神经网络的一个子领域,主要关注更深层次的神经网络结构,也就是深层神经网络(Deep Neural Networks,DNNs)。所以,我们需要先搞清楚什么是神经网络!
1. 感知神经网络
神经网络(Neural Networks)是一种模拟人脑神经元网络结构的计算模型,用于处理复杂的模式识别、分类和预测等任务。生物神经元如下图: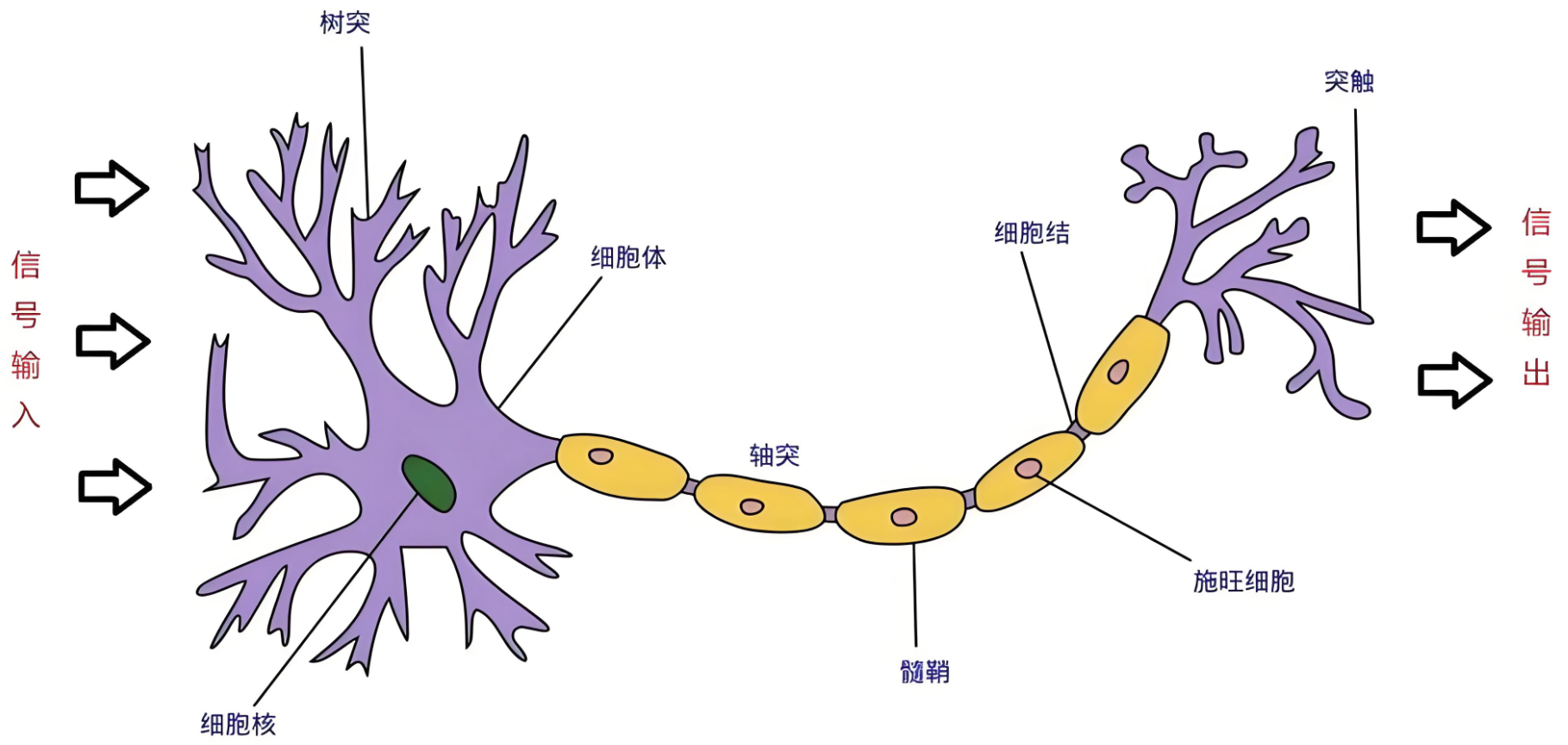
生物学:
人脑可以看做是一个生物神经网络,由众多的神经元连接而成
-
树突:从其他神经元接收信息的分支
-
细胞核:处理从树突接收到的信息
-
轴突:被神经元用来传递信息的生物电缆
-
突触:轴突和其他神经元树突之间的连接
人脑神经元处理信息的过程:
-
多个信号到达树突,然后整合到细胞体的细胞核中
-
当积累的信号超过某个阈值,细胞就会被激活
-
产生一个输出信号,由轴突传递。
神经网络由多个互相连接的节点(即人工神经元)组成。
2. 人工神经元
人工神经元(Artificial Neuron)是神经网络的基本构建单元,模仿了生物神经元的工作原理。其核心功能是接收输入信号,经过加权求和和非线性激活函数处理后,输出结果。
2.1 构建人工神经元
人工神经元接受多个输入信息,对它们进行加权求和,再经过激活函数处理,最后将这个结果输出。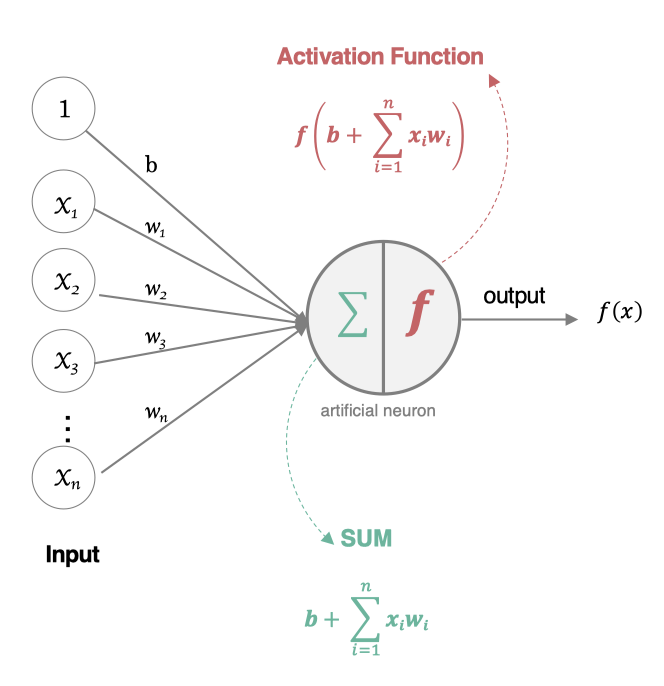
2.2 组成部分
-
输入(Inputs): 代表输入数据,通常用向量表示,每个输入值对应一个权重。
-
权重(Weights): 每个输入数据都有一个权重,表示该输入对最终结果的重要性。
-
偏置(Bias): 一个额外的可调参数,作用类似于线性方程中的截距,帮助调整模型的输出。
-
加权求和: 神经元将输入乘以对应的权重后求和,再加上偏置。
-
激活函数(Activation Function): 用于将加权求和后的结果转换为输出结果,引入非线性特性,使神经网络能够处理复杂的任务。常见的激活函数有Sigmoid、ReLU(Rectified Linear Unit)、Tanh等。
2.3 数学表示
如果有 n 个输入 ,
,
,
,权重分别为
,
,
,
,偏置为 b,则神经元的输出 y 表示为:
其中,是激活函数。
例如:
线性回归:
线性回归不需要激活函数
逻辑回归:
2.4 对比生物神经元
人工神经元和生物神经元对比如下表:
| 生物神经元 | 人工神经元 |
|---|---|
| 细胞核 | 节点 (加权求和 + 激活函数) |
| 树突 | 输入 |
| 轴突 | 带权重的连接 |
| 突触 | 输出 |
3. 深入神经网络
神经网络是由大量人工神经元按层次结构连接而成的计算模型。每一层神经元的输出作为下一层的输入,最终得到网络的输出。
3.1 基本结构
神经网络有下面三个基础层(Layer)构建而成:
-
输入层(Input): 神经网络的第一层,负责接收外部数据,不进行计算。
-
隐藏层(Hidden): 位于输入层和输出层之间,进行特征提取和转换。隐藏层一般有多层,每一层有多个神经元。
-
输出层(Output): 网络的最后一层,产生最终的预测结果或分类结果
3.2 网络构建
我们使用多个神经元来构建神经网络,相邻层之间的神经元相互连接,并给每一个连接分配一个权重,经典如下: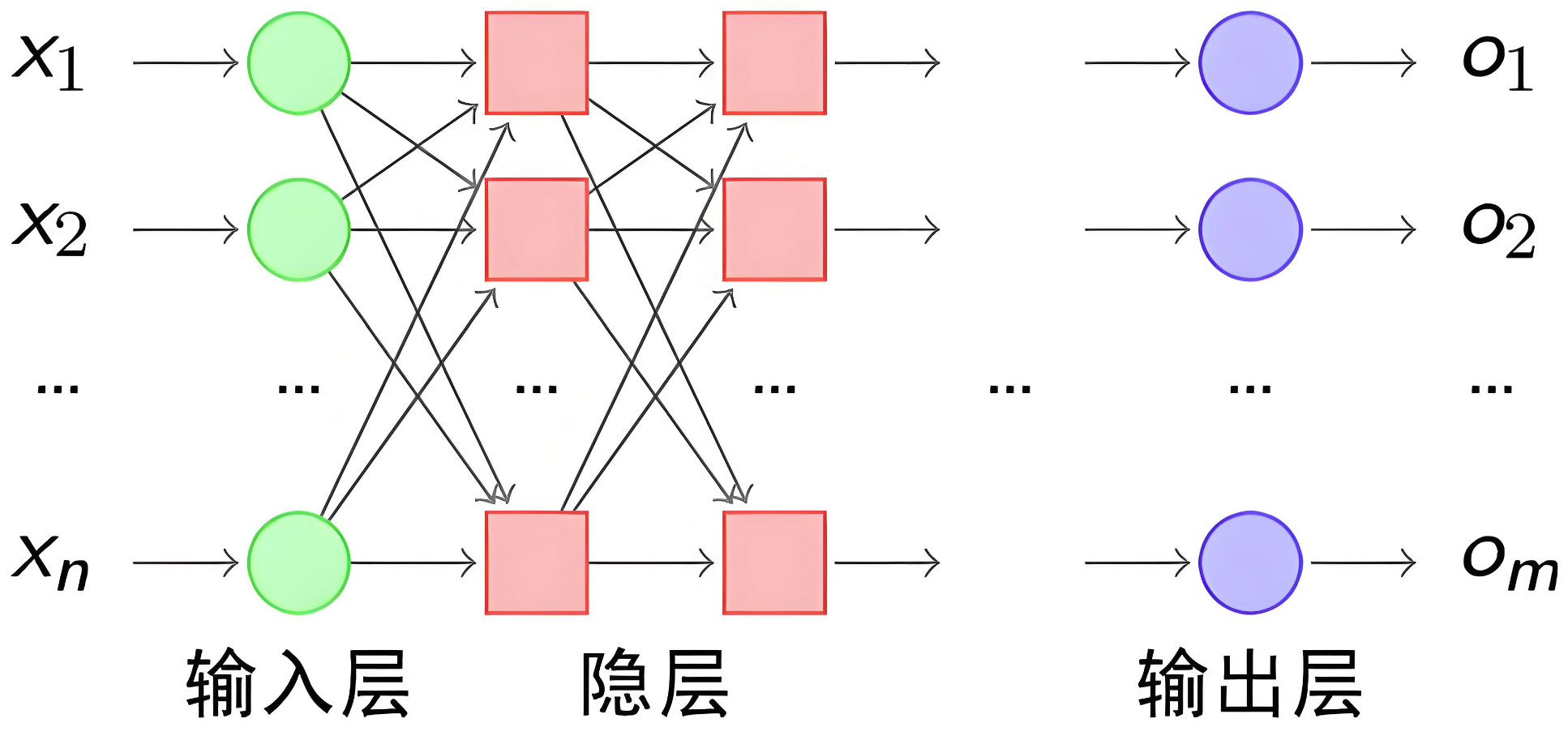
注意:同一层的各个神经元之间是没有连接的。
3.3 全连接神经网络
前馈神经网络(Feedforward Neural Network,FNN)是一种最基本的神经网络结构,其特点是信息从输入层经过隐藏层单向传递到输出层,没有反馈或循环连接。
全连接神经网络(Fully Connected Neural Network,FCNN)是前馈神经网络的一种,每一层的神经元与上一层的所有神经元全连接,常用于图像分类、文本分类等任务。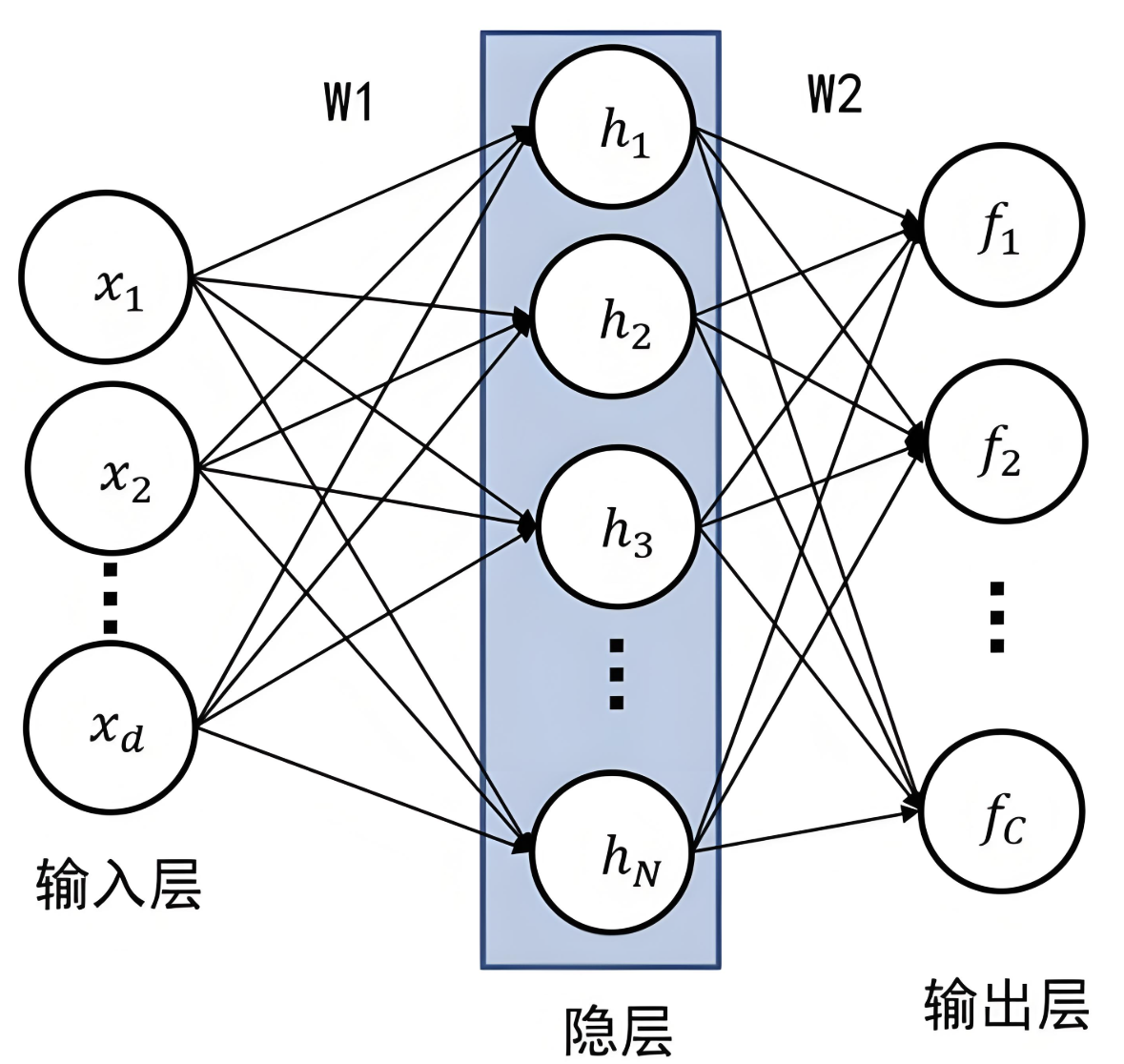
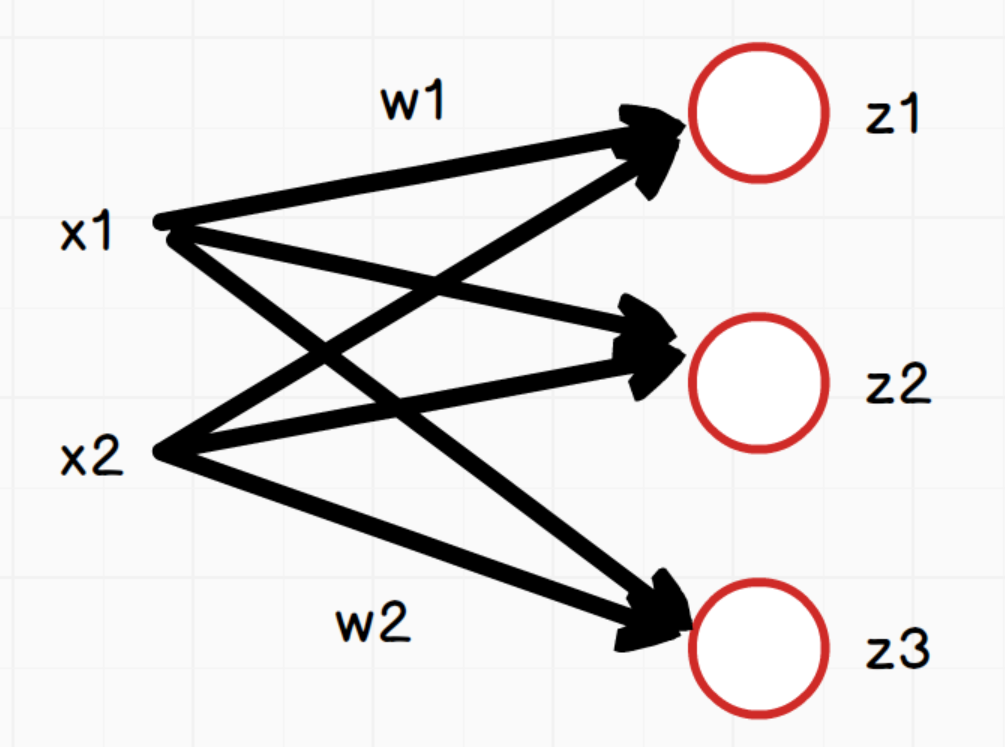
如上图,网络中每个神经元:
说明:三个等式中的w1和w2在这里只是为了方便表示对应x1和x2的权重,实际三个等式中的w值是不同的。
向量x为:
向量w:,其形状为(3,2),3是神经元节点个数,2是向量x的个数
向量z:
向量b:
所以用向量表示为:
-
x是输入数据,形状为 (batch_size, in_features)。
-
W是权重矩阵,形状为 (out_features, in_features)。
-
b是偏置项,形状为 (out_features,)。
-
z是输出数据,形状为 (batch_size, out_features)。
3.3.1 特点
-
全连接层: 层与层之间的每个神经元都与前一层的所有神经元相连。
-
权重数量: 由于全连接的特点,权重数量较大,容易导致计算量大、模型复杂度高。
-
学习能力: 能够学习输入数据的全局特征,但对于高维数据却不擅长捕捉局部特征(如图像就需要CNN)。
3.3.2 计算步骤
-
数据传递: 输入数据经过每一层的计算,逐层传递到输出层。
-
激活函数: 每一层的输出通过激活函数处理。
-
损失计算: 在输出层计算预测值与真实值之间的差距,即损失函数值。
-
反向传播(Back Propagation): 通过反向传播算法计算损失函数对每个权重的梯度,并更新权重以最小化损失。
3.3.3 基本组件认知
先初步认知,他们用法基本一样的,后续在学习深度神经网络和卷积神经网络的过程中会很自然的学到更多组件!
官方文档:torch.nn — PyTorch 2.8 documentation
线性层组件
nn.Linear是 PyTorch 中的一个非常重要的模块,用于实现全连接层(也称为线性层)。它是神经网络中常用的一种层类型,主要用于将输入数据通过线性变换映射到输出空间。
torch.nn.Linear(in_features, out_features, bias=True)
参数说明:
in_features:
-
输入特征的数量(即输入数据的维度)。
-
例如,如果输入是一个长度为 100 的向量,则 in_features=100。
out_features:
-
输出特征的数量(即输出数据的维度)。
-
例如,如果希望输出是一个长度为 50 的向量,则 out_features=50。
bias:
-
是否使用偏置项(默认值为 True)。
-
如果设置为 False,则不会学习偏置项。
示例:构建3层全连接神经网络:在__init__方法中定义网络结构,在forward定义前向传播
import torch
from torch import nn
# 定义全连接神经网络模型
class MyFcnn(nn.Module):
def __init__(self, input_size,out_size):
# 父类初始化
super(MyFcnn, self).__init__()
# 定义线性层1
self.fc1 = nn.Linear(input_size, 64)
# 定义线性层2,输入要和第一层的输出一致
self.fc2 = nn.Linear(64, 32)
# 定义线性层3,输入要和第二层的输出一致
self.fc3 = nn.Linear(32, out_size)
def forward(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
input_size = 32
out_size = 1
model = MyFcnn(input_size,out_size)
print(model)如果模型中线性层按顺序叠加,也可以使用nn.Sequential构建模型。nn.Sequential 是一个顺序容器,内置了自动的前向传播逻辑,它会自动将输入数据依次传递给其中的每一层,并执行前向传播,不需要显式定义 forward() 方法。
import torch
from torch import nn
input_size = 32
# 定义全连接神经网络模型
model = nn.Sequential(
nn.Linear(input_size, 64),
nn.Linear(64, 32),
nn.Linear(32, 1)
)
print(model)激活函数组件
激活函数的作用是在隐藏层引入非线性,使得神经网络能够学习和表示复杂的函数关系,使网络具备非线性能力,增强其表达能力。
常见激活函数:
sigmoid函数:
import torch.nn.functional as F sigmoid = F.sigmoid()
tanh函数:
tanh = F.tanh
ReLU函数:
import torch.nn as nn relu = nn.ReLU()
LeakyReLU函数:
leaky_relu = nn.LeakyReLU(negative_slope=0.01)
softmax函数:
softmax = F.softmax
损失函数组件
损失函数的主要作用是量化模型预测值(y^)与真实值(y)之间的差异。通常,损失函数的值越小,表示模型的预测越接近真实值。训练过程中,通过优化算法(如梯度下降)最小化损失函数,从而调整模型的参数。
PyTorch已内置多种损失函数,在构建神经网络时随用随取!
文档:torch.nn — PyTorch 2.8 documentation
根据任务类型(如回归、分类等),损失函数可以分为以下几类:
回归任务的损失函数:
1.均方误差损失(MSE Loss)
-
函数: torch.nn.MSELoss
import torch.nn as nn loss_fn = nn.MSELoss()
2.L1 损失(L1 Loss)
也叫做MAE(Mean Absolute Error,平均绝对误差)
-
函数: torch.nn.L1Loss
import torch.nn as nn loss_fn = nn.L1Loss()
分类任务的损失函数:
1.交叉熵损失(Cross-Entropy Loss)
-
函数: torch.nn.CrossEntropyLoss
cross_entropy_loss = nn.CrossEntropyLoss()
-
参数:reduction:mean-平均值,sum-总和
-
适用场景: 用于多分类任务。
2.二元交叉熵损失(Binary Cross-Entropy Loss)
-
函数: torch.nn.BCELoss 或 torch.nn.BCEWithLogitsLoss
bce_loss = nn.BCELoss() bce_with_logits_loss = nn.BCEWithLogitsLoss()
-
适用场景: 用于二分类任务。
-
特点: BCEWithLogitsLoss 更稳定,因为它结合了 Sigmoid 激活函数和 BCE 损失。
-
注意:使用
nn.BCELoss时,需要确保预测值经过sigmoid函数处理。如果预测值是 logits(即未经sigmoid处理的预测值),可以使用nn.BCEWithLogitsLoss,它内部会自动应用sigmoid函数。
优化器
官方文档:torch.optim — PyTorch 2.8 documentation
在PyTorch中,优化器(Optimizer)是用于更新模型参数以最小化损失函数的核心工具。
PyTorch 在 torch.optim 模块中提供了多种优化器,常用的包括:
-
SGD(随机梯度下降)
-
Adagrad(自适应梯度)
-
RMSprop(均方根传播)
-
Adam(自适应矩估计)
核心方法有:
zero_grad():清空模型参数的梯度(将梯度置零)。必须在loss.backward()之前调用zero_grad(),避免梯度累积。
step():参数更新;是优化器的核心方法,用于根据计算得到的梯度更新模型参数。优化器会根据梯度和学习率等参数,调整模型的权重和偏置。
以SGD(随机梯度下降)优化器为例:
import torch
import torch.nn as nn
import torch.optim as optim
# 优化方法SGD的学习
def test003():
model = nn.Linear(20, 60)
criterion = nn.MSELoss()
# 优化器:更新模型参数
optimizer = optim.SGD(model.parameters(), lr=0.01)
input = torch.randn(128, 20)
output = model(input)
# 计算损失及反向传播
loss = criterion(output, torch.randn(128, 60))
# 梯度清零
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新模型参数
optimizer.step()
print(loss.item())
if __name__ == "__main__":
test003()-
optim.SGD():优化器方法;是 PyTorch 提供的随机梯度下降(Stochastic Gradient Descent, SGD)优化器。
-
model.parameters():模型参数获取;是一个生成器,用于获取模型中所有可训练的参数(权重和偏置)。
注意:这里只是组件认识和用法演示,没有具体的模型训练功能实现
技术分享是一个相互学习的过程。关于本文的主题,如果你有不同的见解、发现了文中的错误,或者有任何不清楚的地方,都请毫不犹豫地在评论区留言。我很期待能和大家一起讨论,共同补充更多细节。




















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








