机器学习之----线性回归推导

样本

工资	年龄	额度
4000	25	20000
8000	30	70000
5000	28	35000
7500	33	50000
12000	40	85000

例子

数据：工资和年龄（2个特征）
目标：预测银行会贷款给我多少钱（标签）
考虑：工资和年龄都会影响最终银行贷款的结果那么他们各自有多大的影响呢？

线性回归定义（来自于百度百科）

性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

个人理解：线性回归就是通过样本得出一个数值 例如 通过工资和年龄得出可贷款额度。

---

推理开始

假设
X1 = 年龄
X2 = 工资
Y = 银行最终会借多少钱给客户
如下图

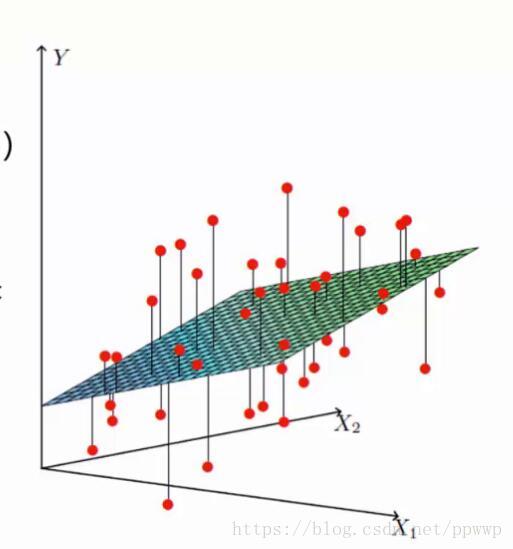
找到最合适的一条线（想象一个高维–面）来最好的拟合我们的数据点

引入数学公式

假设θ₁是年龄的参数，θ₂是工资的参数。

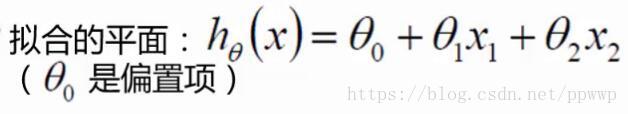
如果θ₁ = 0.1 ，θ₂ = 0.5
hθ(x) = θ + θ₁x₁+θ₂xθ₂ = θ + 0.1*25 + 0.5*4000
参数一旦确定，贷款额度不仅和工资和年龄有关系，贷款额度的上升下降还会会随着偏置项提升下降。

其实θ 的下标是0 ，θx 的x下标是0 且x=1 这样就算是乘以一个1 结果值还是不变。（在实际的工作中，分析数据的时候会额外的增加一个列，这个列里面全部都是1 就是为了如下这个公式）
hθ(x) = θ + θ₁x₁+θ₂xθ₂ = θx + θ₁x₁+θ₂xθ₂
推理出：如下公式

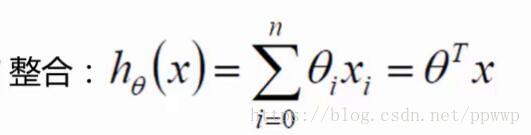
T相当于转置
例如 ： θ 为 [θ0,θ1,θ2]
转置之后为
[[θ0]，
[θ1]，
[θ2]
]
转置之后的矩阵乘以X 的矩阵 [x0,x1,x2]
得出的结果为θ0*x0+θ1*x1+θ2*x2
矩阵相乘 得出最后的结果

误差

对于上面的公式可以推出相应的预测值，但是预测值和真实值还是有一定的差异，就是所谓的误差（用ε来表示该误差）。

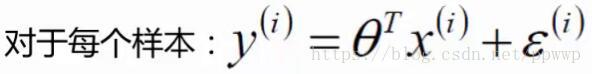
y就是真实值 = θTx 就是预测值 + ε 是误差

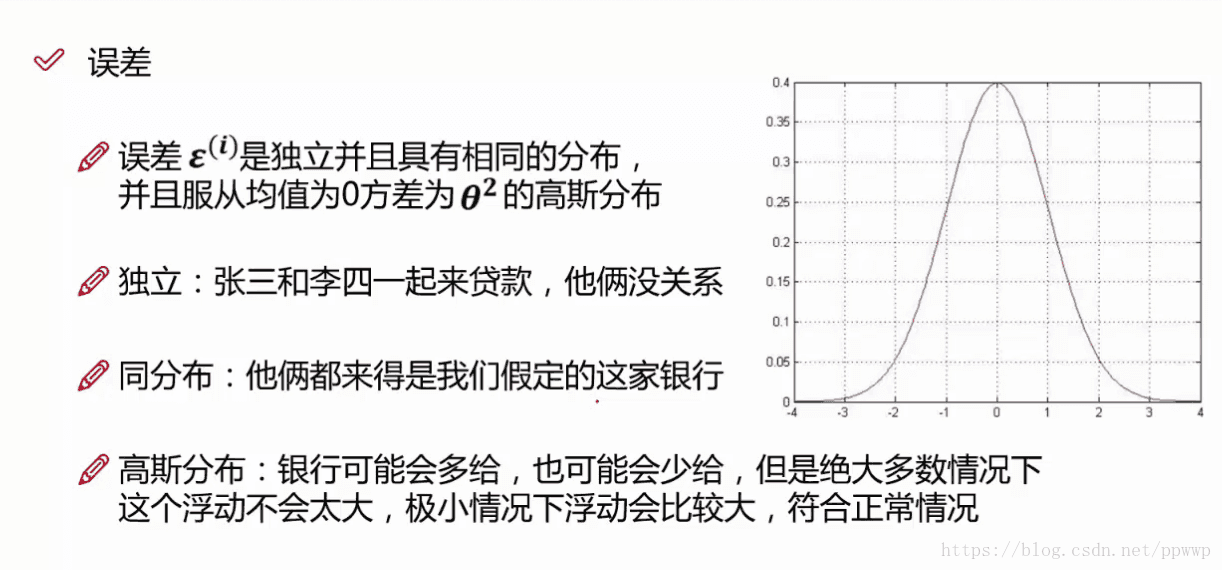
独立：每个样本都是独立的之间互不影响。
同分布：必然是同一个纬度下的数据。比如同一个银行才有效。
高斯分布：如上图右边就是一个 高斯分布的坐标图。大多数的情况就是不多贷不少贷，在向两边扩展的时候，贷的越多或者越少的情况是概率越来越小。


似然函数：寻找参数（L(θ)越大越好）似然函数的最大的时候自然（求参数）估计
对数似然：把上面的似然函数编程 （乘法） 编程下面 对数似然 （两边同时加了log）但是 y=logA*B = logA+logB，所以顺利成章，把乘法变成了加法+

注：log 和exp抵消
最终结果极大估计
所以如下公式越小越好 ，越接近0越好

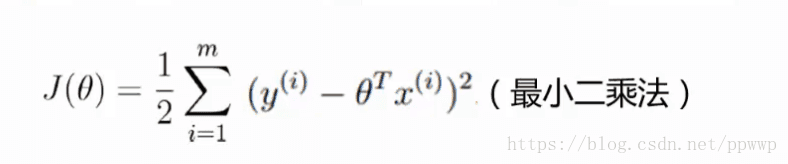
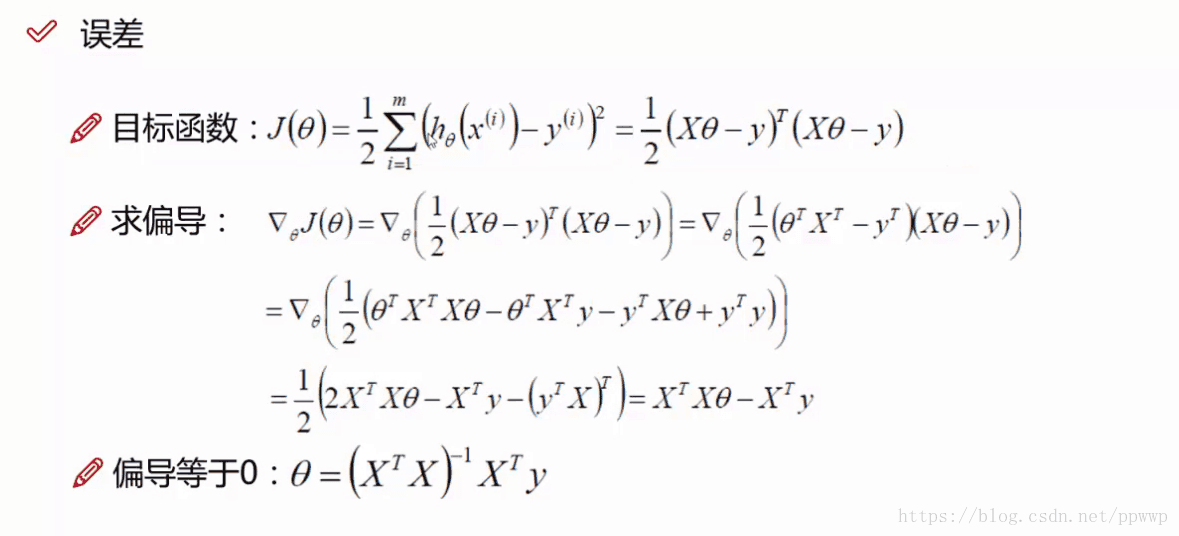
注：转置的应用求和 X平方等于 XT*X

未完。。。