2020牛客寒假算法基础集训营6-图

2020牛客寒假算法基础集训营6-图

好题

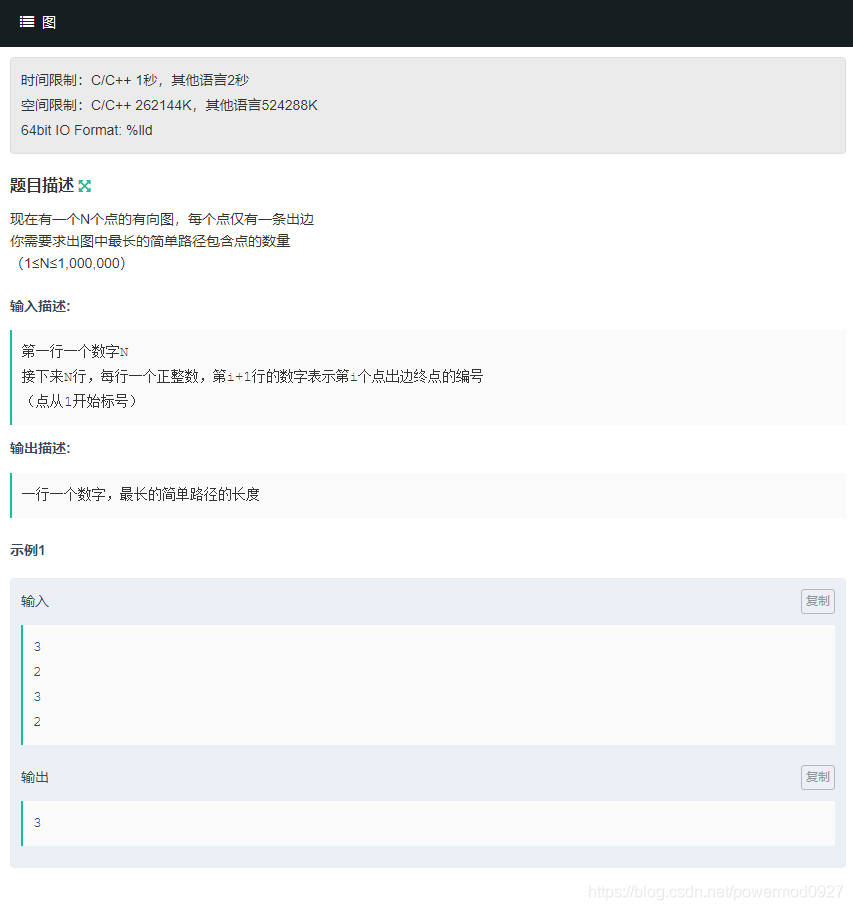
主要坑点在于有可能不是连通图。
那么对于一个连通图来说，肯定是一个环+n条链，那么最大值就是链的长度+环的大小。
所以可以先拓扑排序，把所有链都标记（剩下没有标记的点肯定在环上）。拓扑排序过程中dp存的值是dp【v】=max（dp【u】+1，dp【v】）表示该点最长延伸的长度（v有可能是环上的点这样ans=dp【v】+v所在环的长度-1）
之后dfs没有被标记的点，统计每个环的大小即可

#pragma GCC optimize(3,"Ofast","inline")    //G++
#include<bits/stdc++.h>
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define fcout cout<<setprecision(4)<<fixed
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
 
 
const int inf=0x3f3f3f3f;
const ll INF=0x7fffffffffffffff;
const int mod=1e9+7;
const int maxn = 1e6+5;
const double eps=1e-8;
 
template<typename T> void read(T &x){
    x = 0;char ch = getchar();ll f = 1;
    while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
    while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args) {
    read(first);
    read(args...);
}
int sgn(double a){
    return a<-eps?-1:a<eps?0:1;
}
 
//inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline int sub(int x,int y){return x-y<0?x-y+mod:x-y;}
inline int mul(int x,int y){return 1ll*x*y%mod;}
inline int sq(int x){return 1ll*x*x%mod;}
int pow(int a,int b){return b == 0?1:( b&1?mul(a,sq(pow(a,b/2))):sq(pow(a,b/2)));}
 
vector<int>edge[maxn];
int n;
int in[maxn],to[maxn],vis[maxn],dp[maxn];
void add(int x,int y){
    edge[x].push_back(y);
}
void tupo(){
    queue<int>q;
    for(int i=1;i<=n;i++){
        dp[i]=1;
        if(!in[i]) q.push(i);
    }
    while(!q.empty()){
        int u=q.front();q.pop();
        vis[u]=1;
        for(auto v:edge[u]){
            dp[v]=max(dp[v],dp[u]+1);
            in[v]--;
            if(!in[v]) q.push(v);
        }
    }
}
int sum,maxx;
void dfs(int u){
 
    vis[u]=1;
    sum++;
    maxx=max(maxx,dp[u]);
    for(auto v:edge[u]){
        if(vis[v]) continue;
        dfs(v);
    }
}
int main()
{
    read(n);
    for(int i=1;i<=n;i++){
        read(to[i]);
        add(i,to[i]);
        in[to[i]]++;
    }
    tupo();
    int ans=0;
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            sum=maxx=0;
            dfs(i);
            ans=max(ans,sum+maxx-1);
        }
    }
    cout<<ans<<"\n";
}

好题

当时比赛写的，，，现在看不懂了，好像是dfs+dfs…

#pragma GCC optimize(3,"Ofast","inline")    //G++
#include<bits/stdc++.h>
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define fcout cout<<setprecision(4)<<fixed
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;


const int inf=0x3f3f3f3f;
const ll INF=0x7fffffffffffffff;
const int mod=1e9+7;
const int maxn = 1e6+5;
const double eps=1e-8;

template<typename T> void read(T &x){
    x = 0;char ch = getchar();ll f = 1;
    while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
    while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args) {
    read(first);
    read(args...);
}
int sgn(double a){
    return a<-eps?-1:a<eps?0:1;
}

//inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline int sub(int x,int y){return x-y<0?x-y+mod:x-y;}
inline int mul(int x,int y){return 1ll*x*y%mod;}
inline int sq(int x){return 1ll*x*x%mod;}
int pow(int a,int b){return b == 0?1:( b&1?mul(a,sq(pow(a,b/2))):sq(pow(a,b/2)));}

vector<int>edge[maxn];
int n,flag,ans,__;
int to[maxn],vis[maxn],dp[maxn],re[maxn],root,siz[maxn],VIS[maxn];
int fin(int x){
    return re[x]==x?x:re[x]=fin(re[x]);
}
void uni(int x,int y){
    int xx=fin(x),yy=fin(y);
    if(xx!=yy)
        re[xx]=yy;
}
void add(int x,int y){
    edge[x].push_back(y);
}
void dfs1(int u,int op){

    vis[u]=op;
    for(auto v:edge[u]){
        if(vis[v]==op&&__){
            root=v;
            __=0;
        }
        if(!vis[v]){
            dfs1(v,op);
        }
    }
    if(flag||root==0){
        return ;
    }
    uni(u,root);
    siz[root]++;
    ans=max(ans,siz[root]);
    VIS[u]=1;
    if(u==root){
        flag=1;
    }
}
int dfs(int u){

   if(dp[u]) return dp[u];
//   vis[u]=1;C
   for(auto v:edge[u]) {

        if(VIS[v]){
            dp[u]=1+siz[fin(v)];
        }
        else
            dp[u]=1+dfs(v);
   }
   return dp[u];
}
int main()
{
    read(n);
    for(int i=1;i<=n;i++){
        re[i]=i;
        read(to[i]);
        add(i,to[i]);
    }
    int _=0;
    for(int i=1;i<=n;i++){
        root=flag=0;
        __=1;
        if(!vis[i]){
            dfs1(i,++_);
        }
    }
    mem(vis,0);
    for(int i=1;i<=n;i++){
        if(!VIS[i])
        {
            dfs(i);
            ans=max(ans,dp[i]);
        }
    }
    cout<<ans<<"\n";
}

还是拓扑排序好写@_@