Codeforces 1060C Maximum Subrectangle

最新推荐文章于 2023-05-21 19:00:36 发布

原创最新推荐文章于 2023-05-21 19:00:36 发布 · 196 阅读

0 ·

CC 4.0 BY-SA版权

ACM 专栏收录该内容

245 篇文章

订阅专栏

本文探讨了一种针对矩阵子集和的优化算法，通过将问题转化为一维数组的子段和乘积，实现了在限制条件下寻找最大面积子矩阵的目标。文章详细介绍了算法的实现过程，包括使用前缀和来高效计算不同长度的子段和。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给你两个一维数组A，B

用这两个数组可以生成一个矩阵C，其中C中的元素是这样定义的：

C[i,j]=A(i)*B(j);

大概能看懂什么意思吧。

然后呢，题目要求这样一个子矩阵，使得子矩阵中每个元素的和加起来不能超过X，而且子矩阵的面积要尽可能的大。

子矩阵的面积就是长X宽。

题意很明确，看起来好像和最大子矩阵和差不多嘛。

但是，本题有一个关键的地方，就是如何将子矩阵的和转化。

反正呢，根据一些神奇的数学trick，你可以将原来的求和表达式转化成如下的模式:

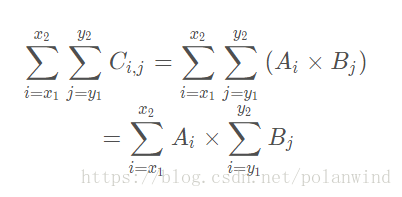
没错，就是这样子。

但是转化成这样有什么用呢?当然有用啦！

我们再来看一下题目要求：

1、子矩阵的和不能超过X

2、子矩阵的面积尽可能最大

而我们的子矩阵和转化成了两个一维数组的子段和的乘积，其中子段的长度不就是子矩阵的长和宽吗？

OK，接下来我们需要做什么呢？没错，我们只需要找到两个一维数组A和B，它们在不同长度上的子段和的最小值就可以了。

因为我们只考虑矩阵的面积，所以要求长和宽都尽可能的要大，同时又要求和不能超过X，所以子段和要尽可能小。

知道了它们在不同长度上的子段和后，只要找到一个满足子矩阵和不超过X的最大值就好了。

语言表述能力还是很辣鸡哈233333，感觉像说了半天废话。

哦对了，在处理不同长度上的子段和的时候可以用前缀和。

#define  _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <algorithm>
#include <deque>
#include <iostream>
#include <string>
#include <math.h>

using namespace std;

long long n, m, x;

long long tempn[2005];
long long tempm[2005];
long long suffn[2005];
long long suffm[2005];
long long costn[2005];
long long costm[2005];

int main() {
	scanf("%lld %lld", &n, &m);
	for (int i = 1;i <= n;++i) {
		scanf("%lld", &tempn[i]);
	}
	for (int i = 1;i <= m;++i) {
		scanf("%lld", &tempm[i]);
	}
	scanf("%lld", &x);
	
	for (int i = 1;i <= n;++i) {
		suffn[i] = suffn[i - 1] + tempn[i];
	}
	for (int i = 1;i <= m;++i) {
		suffm[i] = suffm[i - 1] + tempm[i];
	}

	long long mymin = 2005;
	long long mysum = 0;
	for (int i = 1;i <= n;++i) {
		mysum += tempn[i];
		if (mymin > tempn[i]) {
			mymin = tempn[i];
		}
	}
	costn[1] = mymin;
	costn[n] = mysum;
	
	mymin = 2005;
	mysum = 0;
	for (int i = 1;i <= m;++i) {
		mysum += tempm[i];
		if (mymin > tempm[i]) {
			mymin = tempm[i];
		}
	}
	costm[1] = mymin;
	costm[m] = mysum;
	
	int k = 2;
	while (k <= n - 1) {
		mymin = 4000000;
		for (int i = k;i <= n;++i) {
			if (mymin > (suffn[i] - suffn[i - k])) {
				mymin = suffn[i] - suffn[i - k];
			}
		}
		costn[k] = mymin;
		k++;
	}

	k = 2;
	while (k <= m - 1) {
		mymin = 4000000;
		for (int i = k;i <= m;++i) {
			if (mymin > (suffm[i] - suffm[i - k])) {
				mymin = suffm[i] - suffm[i - k];
			}
		}
		costm[k] = mymin;
		k++;
	}

	long long ans = 0;
	for (int i = n;i >= 1;--i) {
		for (int j = m;j >= 1;--j) {
			if (costn[i] * costm[j] <= x) {
				if (ans < i*j) {
					ans = i*j;
					break;
				}
			}
		}
	}
	printf("%lld\n", ans);
	//system("pause");
	return 0;
}