7-4 余弦函数

#include <stdio.h>
#include <math.h>

#define pi 3.1415926535897932

int main()
{
    double x, t, p, y, epsilon;
    int d = 0;
    scanf("%lg%lg", &x, &epsilon);
    t = fmod(x, 2.0 * pi);
    p = 1.0;
    y = p;
    do
    {
        d += 2;
        p = p * (-t * t) / ((d - 1.0) * d);
        y += p;
    }
    while (fabs(p) >= epsilon);
    printf("%f\n", y);
    return 0;
}

分数 18

全屏浏览

切换布局

作者 李祥

单位 湖北经济学院

根据麦克劳林公式计算任意角的余弦。

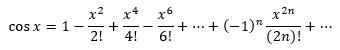
输入格式

x  ε

注：x 为角（单位：弧度），ε 为计算精度。

输出格式

y

注：y 为 x 的余弦值。用 %f 格式限定符输出 6 位小数。

输入样例1

1.047197551196598 0.00000001

输出样例1

0.500000

输入样例2

315.2064629101759 0.000001

输出样例2

0.500000

要求：所计算的最后一项的绝对值恰好小于 ε。

注：pi=3.1415926535897932384626...。

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

栈限制

8192 KB