Coarse-to-Fine Reasoning for Visual Question Answering

面向视觉问答的由粗到细推理方法

一、创新点

1. 提出了一个简单但有效的框架来从问题和图像中提取有意义的特征和谓词（predicate） 。

    提取的信息可以用来解释深度网络的决策。

2. 引入了一种新的由粗到细的推理（Coarse-to-Fine Reasoning）方法 ， 以弥合问题和预测答案时的图像。

  （谓词：关于图像/问题的对象、关系或属性的关键字。）

二、方法

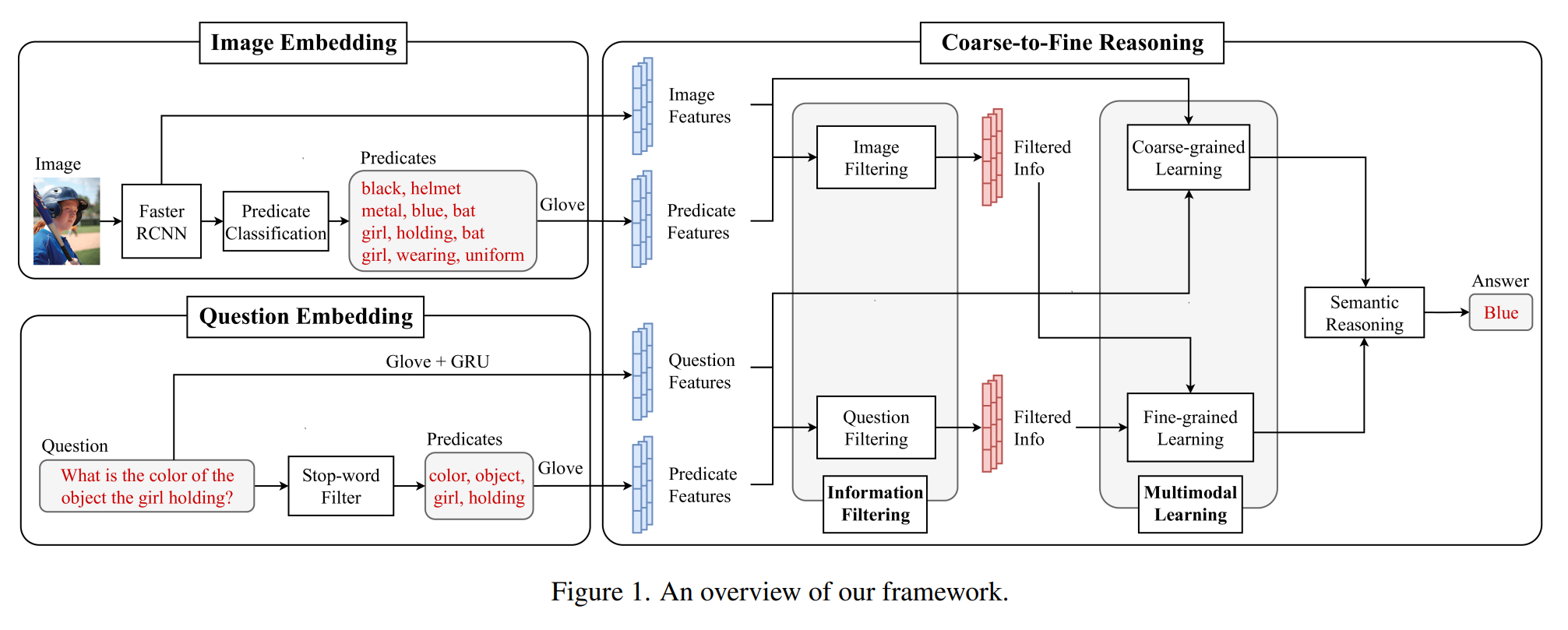
 三、过程

1. 图像嵌入

       保留了原始的Faster R-CNN 多任务损失用于目标检测，然后为属性类预测器和关系类预测器 增加了两个额外的交叉熵损失。然后，将提取的对象以及它们的属性和关系重新排列，形成谓词。

       每个谓词遵循三种形式中的一种:

              （1）单谓词<obj>;

              （2）基于属性的谓词<attr,obj> ;

              （3）和基于关系的谓词<obj1,rel,obj2>。

       对于每个谓词中的每个单词，本文应用300-dim Glove word embedding来提取谓词特征。

2. 问题嵌入

       为了提取问题特征，本文应用了600-dim Glove词嵌入伴随GRU来提取特征并学习问题中所有单词的依赖关系。

       为了提取问题谓词，本文将整个问题通过一个停用词过滤器（stop-word filter） 。然后对于每 个问题谓词中的每个词，应用 300-dim Glove word embedding来提取谓词特征。

       （这个过滤器是两个列表的组合 。 第一个列表包含基于NLTK的停用词列表中的单词，即在 句子中不添加太多含义的单词。第二个列表包含出现频率小于10的所有问题中的单词 。 第二个列 表中的单词被认为是罕见词， 对于模型来说很难学习。）

3. 粗到细推理

    3.1 信息过滤

       信息过滤以特征和谓词作为输入。f 和 p 都是矩阵形式; nf , np 表示实例的数量(例如，roi的数量或谓词的数量);df, dp表示每个实例的维数。为了过滤掉特征 f 中的不必要信息，将谓词p作为监督信息。通过这种相互作用机制，计算一个加权映射