本文探讨了Catalan数在不同场景下的应用，包括连接问题、树的构造以及购票问题，展示了其在计算机科学领域的广泛用途。
给定N*2个点，求分别将其两两相连，每个点仅链接一次，而且每条线段不相交！
题目分析：
这又是Catalan数
直接套公式吧，其实证明目前我还没会，嘎嘎
公式：
f[n]=![$$\sum_{k=0}^{n-1}{{f[n-1-k]*f[k]}}$$](https://i-blog.csdnimg.cn/blog_migrate/cb8ac874d88f9b7504fa219d8d3af04e.png "$$\sum_{k=0}^{n-1}{{f[n-1-k]*f[k]}}$$")
;
直接计算就可以了，这里设计到大数的运算，我是用JAVA写的，不想用C模拟了 呵呵
代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import
java.io.*;
import
java.util.*;
import
java.math.*;
public
class
Main {
public
static
void
main(
String
args[]){
List list=
new
ArrayList(
102
);
BigInteger f=BigInteger.valueOf(
1
);
list.add(f);
list.add(f);
f=BigInteger.valueOf(
2
);
list.add(f);
for
(
int
i=
3
;i<=
100
;i++){
BigInteger sum=BigInteger.valueOf(
0
);
for
(
int
j=
0
;j<i;j++){
sum=sum.add( ((BigInteger)list.
get
(i-
1
-j)).multiply( ((BigInteger) list.
get
(j) )) );
}
list.add(sum);
}
Scanner cin=
new
Scanner(System.
in
);
int
n;
while
(cin.hasNext()){
n=cin.nextInt();
if
(n==-
1
)
break
;
System.out.println(list.
get
(n));
}
}
}
|
题目大意：上面有一篇关于二叉树的构造方法数，这里只是普通的树，所以不用考虑次序。
Catalan数可以表示二叉树的构造方法数，Catalan数=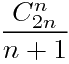
但是在这里我们不需要考虑次序，所以我们要乘以A(N,N);也就是N种元素的排列方法 也就是N！
所以这里的方法数=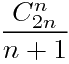*A（N，N）；
化简一下：
(n+2)*(n+3)*(n+4)*...*(2*n)
但是我这里直接把各个部分直接求出来的 嘿嘿，因为用JAVA写方便呀 所以都无所谓的啦
代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
import
java.io.*;
import
java.util.Scanner;
import
java.math.BigInteger;
public
class
Main{
public
static
BigInteger C(
int
n,
int
m){
BigInteger sum=BigInteger.valueOf(
1
);
for
(
int
i=n;i>n-m;i--)
sum=sum.multiply(BigInteger.valueOf(i));
for
(
int
j=
1
;j<=m;j++)
sum=sum.divide(BigInteger.valueOf(j));
return
sum;
}
public
static
BigInteger jie(
int
n){
BigInteger sum=BigInteger.valueOf(
1
);
for
(
int
i=
1
;i<=n;i++)
sum=sum.multiply(BigInteger.valueOf(i));
return
sum;
}
public
static
void
main(
String
args[]){
int
n;
Scanner cin=
new
Scanner(System.
in
);
while
(cin.hasNext()){
n=cin.nextInt();
if
(n==
0
)
break
;
BigInteger t1=C(
2
*n,n);
BigInteger t2=jie(n);
t1=t1.divide(BigInteger.valueOf(n+
1
));
t1=t1.multiply(t2);
System.out.println(t1);
}
}
}
|
题目大意：M+N个人排队买票，票的单价是50￥，每个人只能买一张。 M个人拿50的去买，N个人拿100的去买，然后悲剧的是售票处开始的时候没有钱，所以如果拿100块买票人前面的拿50块买票的人小于或者等于用100块买票的人，这种排队方式就不合法，也就是不能顺利全部都买到票（因为没零钱找了）！
题目分析：
这是一个Catalan数的非常经典的应用，买票问题，首先我们用"0"表示用50块买票的人，用“1”表示用100块买票的人，然而假设m=4,n=3,的一个序列是：0110100显然，它不合法，然后我们把他稍微变化一下：把第一个不合法的“1”后面的所有数0位为1， 1位为0；这样我们得到了另一个序列：0111011，显然他也不是合法的，但是在这里我们关注的不是他合不合法！只是说明每个不合法的都有一个这样的序列跟他一一对应！
所以我们计算公式就是：合法的排列方式=所有排列方式-非法排列方式
我们这里非法排列方式的计算 就是：(
- 
)*M!*N!，然而在这题，因为每个人都是不同的，所以还要乘以 M！*N！
所以得出最终方程：
F（N）=(-)*M！*N！ ；
然后再化简一下;
F(N)=(M+N)! * (M-N+1)/(M+1)
大数运算模拟，
分别有：
大数阶乘
大数乘小数
大数除小数。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
#
include
<iostream>
#
include
<cstdio>
#
include
<cstring>
#define MAX
201
using
namespace
std;
int
factor[
205
][MAX]={
0
};
int
sim[
201
]={
0
};
int
multiply(
int
s[],
int
Max,
int
b){
//the static number can't be a canliang
int
ans=
0
,i;
for
(i=Max;i>=
1
;i--){
ans+=s[i]*b;
s[i]=ans%
10000
;
ans=ans/
10000
;
}
return
0
;
}
int
div(
int
s[],
int
Max,
int
b){
int
ans=
0
,t,i;
for
(i=
1
;i<=Max;i++){
t=ans*
10000
+s[i];
s[i]=t/b;
ans=t%b;
}
return
0
;
}
int
getfactor(){
int
i;
factor[
0
][MAX-
1
]=factor[
1
][MAX-
1
]=
1
;
for
(i=
2
;i<=
203
;i++){
memcpy(factor[i],factor[i-
1
],MAX*sizeof(
int
));
//this has a falut that i have replace memcpy by strcpy!
multiply(factor[i],MAX-
1
,i);
}
return
0
;
}
int
output(
int
*s,
int
k){
int
i=
1
;
printf(
"Test #%d:\n"
,k);
while
(s[i]==
0
&&i<MAX)
i++;
printf(
"%d"
,s[i++]);
for
(;i<MAX;i++)
printf(
"%04d"
,s[i]);
printf(
"\n"
);
return
0
;
}
int
main(){
int
m,n,i,k=
1
;
getfactor();
while
(scanf(
"%d %d"
,&m,&n),m+n){
memcpy(sim,factor[m+n],sizeof(
int
)*MAX);
/*for(i=1;i<=MAX;i++){
for(int j=1;j<MAX;j++)
cout<<factor[i][j];
cout<<endl;
}*/
if
(n>m){
printf(
"Test #%d:\n"
,k++);
printf(
"0\n"
);
//别忘记了 判断这种情况，
//当初为了这个BUG找了好苦，5555....
continue
;
}
multiply(sim,MAX-
1
,m-n+
1
);
div(sim,MAX-
1
,m+
1
);
output(sim,k);
k++;
}
return
0
;
}
|
题目大意：就是给你1到N个数，让你求他能构成多少种二叉树；
题目分析：这里又是一种组合数学里的重要知识点！Catalan数的应用。
如果数据比较小，建议模拟这个公式：
Catalan的原始递推公式就是这个，这个是专门针对给出节点，有多少二叉数构造方法的方程。
=
+
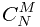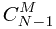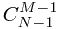
用二维数组模拟，当前元素的值等于他正上方的值+左边的值；
当然所消耗的内存是很大的 ：M*N*4 Bytes,所以数字小才能模拟50以内比较保险 哈哈{^_^}！
然后大数的就只有应用到大数的算法啦，反正我认为C++里的模拟太费事了 ，所以今天第一次也学习写
JAVA里的大数的运算了， 建议您也学学，嘿嘿，方便啊 。
首先分析一下思路：
这个方程进一步化简：
F( N )=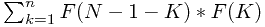
（k=0....N-1）
根据这个公式进行计算就可以了
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
import
java.math.*;
import
java.util.*;
public
class
Main{
public
static
void
main(
String
args[]){
List list=
new
ArrayList(
101
);
BigInteger f=BigInteger.valueOf(
1
);
list.add(f);
list.add(f);
for
(
int
i=
2
;i<=
100
;i++){
f=BigInteger.valueOf(
0
);
for
(
int
j=
0
;j<i;j++)
f=f.add(((BigInteger)list.
get
(j)).multiply( (BigInteger)list.
get
(i-
1
-j)));
list.add(f);
}
Scanner cin=
new
Scanner(System.
in
);
int
inputInt=
0
;
while
(cin.hasNext()){
inputInt=cin.nextInt();
System.out.println(list.
get
(inputInt));
}
}
}
|
扫一扫
2667
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
