卷积核为1的一维卷积，等价于全连接，个人理解

最近在看pointNet语义分割的代码，其中有一处令我很困惑，明明论文中使用的是MLP，但是为什么代码中使用的却是卷积核为1的一维卷积呢？难道二者是等价的吗？

这个问题困扰了我好久，网上也没有搜到类似的答案，后来自己才想到的，现总结如下：

以
这个语句为例子，假设输入的点云数据的tensor是n（batch）×1088（通道，也叫特征）×4096（点云个数），那么在卷积核为1的卷积过程中发生了什么呢？我自己画了张图，对于每一个卷积核，卷积后都生成了1×4096的图层，一共512个图层，合在一起就是512×4096

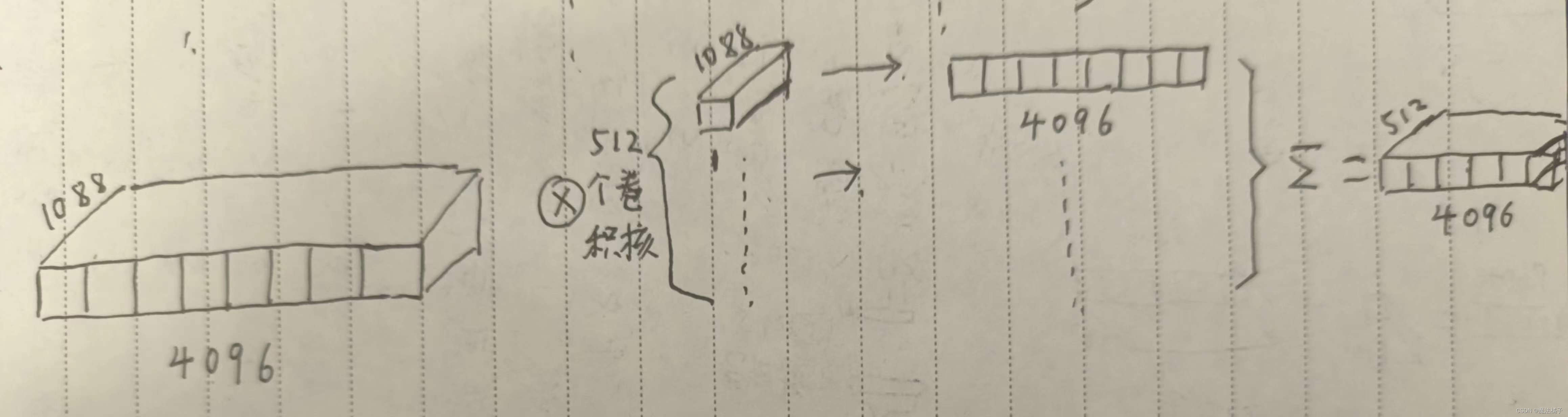
这么看是没有MLP的，但是对于单个的点来说，每个点的1088个特征都和卷积核做了卷积操作，所以这对于单个点来说，其实是相当于MLP的全连接的。

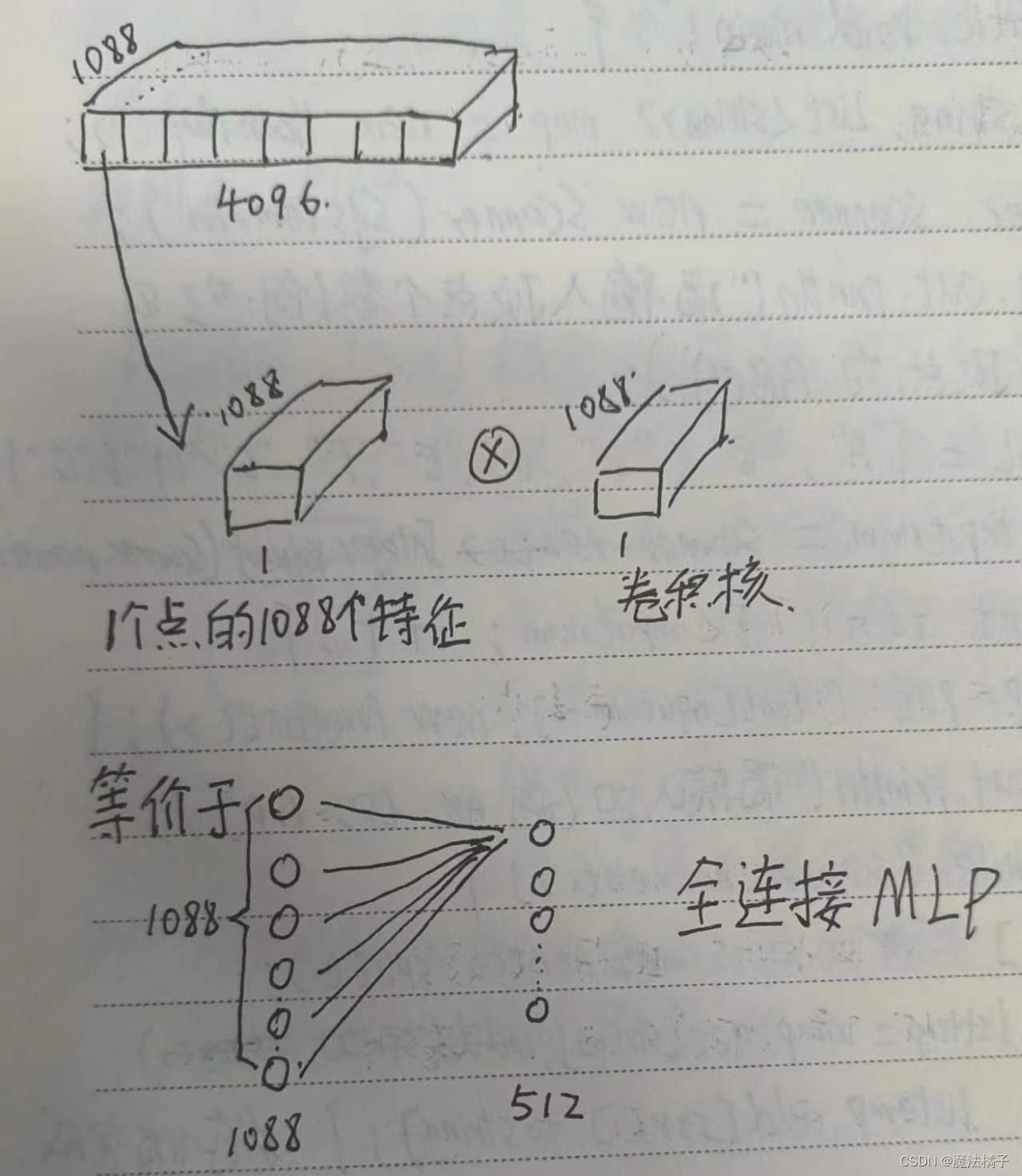
所以这里是相当于使用卷积核为1的一维卷积操作，同时对n*4096个点做全连接操作。
个人理解，仅供参考。

--------------------------------------------------------------------------------------
3.1号补充：为什么不问问神奇的Chatgpt呢？