免疫优化算法在物流配送中心选址中的应用

最新推荐文章于 2025-05-16 14:00:49 发布

小明带你做优化

最新推荐文章于 2025-05-16 14:00:49 发布

阅读量2k

点赞数 29

文章标签：算法

本文链接：https://blog.youkuaiyun.com/pgpaojiao/article/details/137235805

版权

物流中心选址问题

随着世界经济的快速发展以及现代科学技术的进步,物流业作为国民经济的一个新兴服务部门,正在全球范围内迅速发展。物流业的发展给社会的生产和管理、人们的生活和就业乃至政府的职能以及社会的法律制度等都带来巨大的影响,因此物流业被认为是国民经济发展的动脉和基础产业,被形象地喻为促进经济发展的“加速器”。
在物流系统的运作中,配送中心的任务就是根据各个用户的需求及时、准确和经济地配送商品货物。配送中心是连接供应商与客户的中间桥梁,其选址方式往往决定着物流的配送距离和配送模式,进而影响着物流系统的运作效率。另外,物流中心的位置一旦被确定,其位置难以再改变。因此,研究物流配送中心的选址具有重要的理论意义和现实应用意义。一般说来,物流中心选址模型是非凸和非光滑的带有复杂约束的非线性规划模型,属NP-hard问题。

免疫优化算法

生物免疫系统是一个高度进化的生物系统,它旨在区分外部有害抗原和自身组织,从而保持有机体的稳定。从计算角度看,生物免疫系统是一个高度并行、分布、自适应和自组织的系统,具有很强的学习、识别和记忆能力。
免疫系统具有如下特征:
(1)产生多样抗体的能力：通过细胞的分裂和分化作用,免疫系统可产生大量的抗体来抵御各种抗原。
(2)自我调节机构：免疫系统具有维持免疫平衡的机制,通过对抗体的抑制和促进作用能自我调节产生适当数量的必要抗体。
(3)免疫记忆功能：产生抗体的部分细胞会作为记忆细胞被保存下来,对于今后侵入的同类抗原,相应的记忆细胞会迅速激发而产生大量的抗体。免疫算法(immune algorithm)正是受生物免疫系统启发,在免疫学理论基础上发展起来的一种新兴的智能计算方法。它利用免疫系统的多样性产生和维持机制来保持群体的多样性,克服了一般寻优过程尤其是多峰函数寻优过程中难处理的“早熟”问题,最终求得全局最优解。与其他智能算法相比,免疫算法的研究起步较晚,其发展历史只有短短二十几年。

Farmer等于1986年率先基于免疫网络学说构造了免疫系统的动态模型,并探讨了免疫系统与其他人工智能方法的联系，从而开创了免疫系统的研究。

免疫算法和遗传算法都是采用群体搜索策略,并且强调群体中个体间的信息交换,因此有许多相似之处,比如两者具有大致相同的算法结构,都要经过“初始种群产生一评价标准计算一种群间个体信息交换一新种群产生”这一循环过程,最终以较大的概率获得问题的最优解;另外,两者本质上具有并行性,具有与其他智能计算方法结合的固有优势等。

免疫算法和遗传算法之间也存在一些区别,主要表现为对个体的评价、选择及产生的方式不同。遗传算法中个体的评价是通过计算个体适应度得到的,算法选择父代个体的唯一标准是个体适应度;而免疫算法对个体的评价则是通过计算亲和度(affinity)得到的,个体的选择也是以亲和度为基础进行的。个体的亲和度包括抗体-抗原之间的亲和度(匹配程度)和抗体-抗体之间的亲和度(相似程度),它反映了真实的免疫系统的多样性,因此免疫算法对个体的评价更加全面,其个体选择方式也更为合理。

此外,遗传算法通过交叉、变异等遗传操作产生新个体,而在免疫算法中,虽然交叉、变异等固有的遗传操作也被广泛应用,但是新抗体的产生还可以借助克隆选择、免疫记忆、疫苗接种等遗传算法中所欠缺的机理,同时免疫算法中还对抗体的产生进行促进或者抑制,体现了免疫反应的自我调节功能,保证了个体的多样性。

本文把免疫优化算法用于物流配送中心选址问题中。在考虑该问题的约束条件和优化目标的基础上,建立了物流配送中心选址问题的数学模型,并采用免疫优化算法求解最佳物流配送中心选址模型。

实际案例

问题描述：

在物流配送中心选址模型中做如下假设:

(1)配送中心的规模容量总可以满足需求点需求,并由其配送辐射范围内的需求量确定;

(2)一个需求点仅由一个配送中心供应;

(3)不考虑工厂到配送中心的运输费用。基于以上假设,建立如下模型。该模型是一个选址/分配模型,在满足距离上限的情况下需要从n个需求点中找出配送中心并向各需求点配送物品。目标函数是各配送中心到需求点的需求量和距离值的乘积之和最小,目标函数为

$minF=\sum_{i\in N}\sum_{j\in M_{i}}\omega_{i}d_{ij}Z_{ij}$

约束条件：

$\begin{gathered} \sum_{j\in M_{i}}Z_{ij}=1,\quad i\in N (1)\\ Z_{ij}\leqslant h_{j},\quad i\in N,\quad j\in M_{i} (2)\\ \sum_{j\in M_{i}}h_{j}=p (3)\\ Z_{ij},h_{j}\in\langle0,1\rangle,\quad i\in N,\quad j\in M_{i} (4) \\ d_{ij}\leqslant s (5) \end{gathered}$

其中,N={1,2,…,n}是所有需求点的序号集合; $M_i$ 为到需求点i的距离小于s的备选配送中心集合, $i\in N,M_{i}\subseteq N$ , $\omega_{i}$ 表示需求点的需求量; $d_{ij}$ 表示从需求点i到离它最近的配送中心j的距离; $Z_{ij}$ 为0-1变量,表示用户和物流中心的服务需求分配关系,当其为1时,表示需求点i的需求量由配送中心j供应,否则 $Z_{ij}$ =0; $h_{j}$ 是0-1变量,当其为1时,表示点j被选为配送中心;s为新建配送中心离由它服务的需求点的距离上限。

式(2)保证每个需求点只能由一个配送中心服务;式(3)确保需求点的需求量只能被设为配送中心的点供应,即没有配送中心的地点不会有客户;式(4)规定了被选为配送中心的数量为p;式(5)表示变量 $Z_{ij}$ 和 $h_{j}$ ,是0-1变量;式(6)保证了需求点在配送中心可配送到的范围内。

算法流程

免疫算法具体实现步骤如下:

(1)分析问题。对问题及其解的特性进行分析,设计解的合适表达形式。
(2)产生初始抗体群。随机产生N个个体并从记忆库中提取m个个体构成初始群体,其中m为记忆库中个体的数量。
(3)对上述群体中各个抗体进行评价。在本算法中对个体的评价是以个体的期望繁殖率P为标准的。
(4)形成父代群体。将初始群体按期望繁殖率P进行降序排列,并取前N个个体构成父代群体;同时取前m个个体存人记忆库中。
(5)判断是否满足结束条件,是则结束;反之,则继续下一步操作。
(6)新群体的产生。基于步骤(4)的计算结果对抗体群体进行选择、交叉、变异操作得到新群体,再从记忆库中取出记忆的个体,共同构成新一代群体。
(7)转去执行步骤(3)。

初始解的产生

如果记忆库非空,则初始抗体群从记忆库中选择生成。否则,在可行解空间随机产生初始抗体群。此处采用简单编码方式。每个选址方案可形成一个长度为p的抗体(p表示配送中心数量),每个抗体代表被选为配送中心的需求点的序列。例如,考虑包含31个需求点的问题。1,2,…,31代表需求点的序号。从中选出6个作为配送中心。抗体[2 7 15 21 29 11]代表一个可行解,它表示2,7,15,21,29,11被选为配送中心。这种编码方式能够满足约束条件式(4)和式(5)。

解的多样性评价

(1)抗体与抗原间亲和力

抗体与抗原之间的亲和力用于表示抗体对抗原的识别程度,此处针对上述配送中心选址模型设计亲和力函数 $A_v$

$A_{v}=\frac{1}{F_{v}}=\frac{1}{\sum_{i\in N}\sum_{i\in M_{i}}\omega_{i}d_{ij}Z_{ij}-C\sum_{i\in N}\min\left\{\left(\sum_{j\in M_{i}}Z_{ij}\right)-1,0\right\} }\quad(7)$

其中, $F_v$ 为目标函数;分母中第二项表示对违反距离约束的解给予惩罚,C取一个比较大的正数

(2)抗体与抗体间亲和力

抗体与抗体之间的亲和力反映了抗体之间的相似程度。此处借鉴由Forrest等提出的R位连续方法计算抗体与抗体间的亲和力。R位连续方法实际是一种部分匹配规则。该方法的关键是确定一个R值,代表亲和度判定的阈值。两种个体编码有超过R位或者连续R位的编码相同,则表示这两种抗体近似“相同”,否则表示两种个体不同。此处抗原的编码方法,各位之间不需考虑排序,可参考变形的R位连续方法计算抗体间亲和度,即

$S_{\mathrm{v},s}=\frac{k_{\mathrm{v},s}}{L} \quad(8)$

(3)抗体浓度

抗体的浓度 $C_v$ 即群体中相似抗体所占的比例,即

$C_{v}=\frac{1}{N}\sum_{j\in N}S_{v,s}\quad(9)$

其中,N为抗体总数；，T为预设值

(4)期望繁殖概率

在群体中,每个个体的期望繁殖概率由抗体与抗原间亲和力 $A_v$ 和抗体浓度 $C_v$ 两部分共同决定，即

$P=\alpha\frac{A_{v}}{\sum A_{v}}+(1-\alpha)\frac{C_{v}}{\sum C_{v}}\quad(10)$

其中, $\alpha$ 为常数。由上式可见,个体适应度越高,则期望繁殖概率越大,个体浓度越大,则期望繁殖概率越小。这样既鼓励了适应度高的个体,同时抑制了浓度高的个体,从而确保了个体多样性。
免疫算法在抑制高浓度个体时,与抗原亲和度最高的个体也可能因其浓度高而受到抑制，从而导致已求得的最优解丢失,因此采取精英保留策略,在每次更新记忆库时,先将与抗原亲和度最高的若干个个体存入记忆库,再按照期望繁殖概率将剩余群体中优秀个体存人记忆库。

4.免疫操作
(1)选择:按照轮盘赌选择机制进行选择操作,个体被选择的概率即为式(10)计算出的期望繁殖概率。
(2)交叉:本文采用单点交叉法进行交叉操作。
(3)变异:采用常用的变异方法,即随机选择变异位进行变异

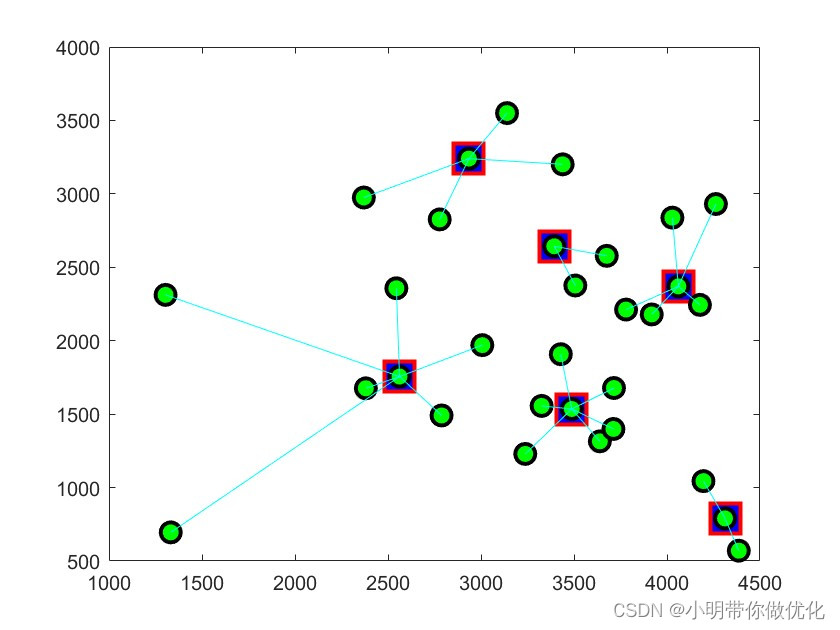
结果

matlab 部分代码如下

%% 免疫优化算法在物流配送中心选址中的应用
%% 清空环境
clc
clear

%% 算法基本参数           
sizepop=50;           % 种群规模
overbest=10;          % 记忆库容量
MAXGEN=100;            % 迭代次数
pcross=0.5;           % 交叉概率
pmutation=0.4;        % 变异概率
ps=0.95;              % 多样性评价参数
length=6;             % 配送中心数
M=sizepop+overbest;

%% step1 识别抗原,将种群信息定义为一个结构体
individuals = struct('fitness',zeros(1,M), 'concentration',zeros(1,M),'excellence',zeros(1,M),'chrom',[]);
%% step2 产生初始抗体群
individuals.chrom = popinit(M,length);
trace=[]; %记录每代最个体优适应度和平均适应度

%% 迭代寻优
for iii=1:MAXGEN

     %% step3 抗体群多样性评价
     for i=1:M
         individuals.fitness(i) = fitness(individuals.chrom(i,:));      % 抗体与抗原亲和度(适应度值）计算
         individuals.concentration(i) = concentration(i,M,individuals); % 抗体浓度计算
     end
     % 综合亲和度和浓度评价抗体优秀程度，得出繁殖概率
     individuals.excellence = excellence(individuals,M,ps);
          
     % 记录当代最佳个体和种群平均适应度
     [best,index] = min(individuals.fitness);   % 找出最优适应度 
     bestchrom = individuals.chrom(index,:);    % 找出最优个体
     average = mean(individuals.fitness);       % 计算平均适应度
     trace = [trace;best,average];              % 记录
     
     %% step4 根据excellence，形成父代群，更新记忆库（加入精英保留策略，可由s控制）
     bestindividuals = bestselect(individuals,M,overbest);   % 更新记忆库
     individuals = bestselect(individuals,M,sizepop);        % 形成父代群

     %% step5 选择，交叉，变异操作，再加入记忆库中抗体，产生新种群
     individuals = Select(individuals,sizepop);                                                             % 选择
     individuals.chrom = Cross(pcross,individuals.chrom,sizepop,length);                                    % 交叉
     individuals.chrom = Mutation(pmutation,individuals.chrom,sizepop,length);   % 变异
     individuals = incorporate(individuals,sizepop,bestindividuals,overbest);                               % 加入记忆库中抗体      

end

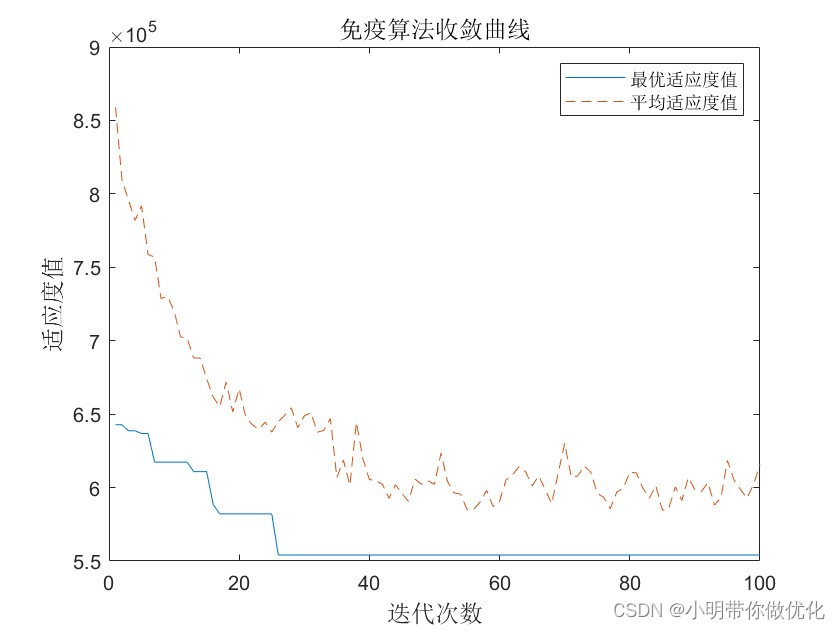
%% 画出免疫算法收敛曲线
figure(1)
plot(trace(:,1));
hold on
plot(trace(:,2),'--');
legend('最优适应度值','平均适应度值')
title('免疫算法收敛曲线','fontsize',12)
xlabel('迭代次数','fontsize',12)
ylabel('适应度值','fontsize',12)

%% 画出配送中心选址图
%城市坐标
city_coordinate=[1304,2312;3639,1315;4177,2244;3712,1399;3488,1535;3326,1556;3238,1229;4196,1044;4312,790;4386,570;
                 3007,1970;2562,1756;2788,1491;2381,1676;1332,695;3715,1678;3918,2179;4061,2370;3780,2212;3676,2578;
                 4029,2838;4263,2931;3429,1908;3507,2376;3394,2643;3439,3201;2935,3240;3140,3550;2545,2357;2778,2826;2370,2975];
carge=[20,90,90,60,70,70,40,90,90,70,60,40,40,40,20,80,90,70,100,50,50,50,80,70,80,40,40,60,70,50,30];
%找出最近配送点
for i=1:31
    distance(i,:)=dist(city_coordinate(i,:),city_coordinate(bestchrom,:)');
end
[a,b]=min(distance');

index=cell(1,length);

for i=1:length
%计算各个派送点的地址
index{i}=find(b==i);
end
figure(2)
title('最优规划派送路线')
cargox=city_coordinate(bestchrom,1);
cargoy=city_coordinate(bestchrom,2);
plot(cargox,cargoy,'rs','LineWidth',2,...
    'MarkerEdgeColor','r',...
    'MarkerFaceColor','b',...
    'MarkerSize',20)
hold on

plot(city_coordinate(:,1),city_coordinate(:,2),'o','LineWidth',2,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor','g',...
    'MarkerSize',10)

for i=1:31
    x=[city_coordinate(i,1),city_coordinate(bestchrom(b(i)),1)];
    y=[city_coordinate(i,2),city_coordinate(bestchrom(b(i)),2)];
    plot(x,y,'c');hold on
end

function fit=fitness(individual)
%计算个体适应度值
%individual    input      个体
%fit           output     适应度值
%城市坐标
city_coordinate=[1304,2312;3639,1315;4177,2244;3712,1399;3488,1535;3326,1556;3238,1229;4196,1044;4312,790;4386,570;
                 3007,1970;2562,1756;2788,1491;2381,1676;1332,695;3715,1678;3918,2179;4061,2370;3780,2212;3676,2578;
                 4029,2838;4263,2931;3429,1908;3507,2376;3394,2643;3439,3201;2935,3240;3140,3550;2545,2357;2778,2826;2370,2975];
%货物量
carge=[20,90,90,60,70,70,40,90,90,70,60,40,40,40,20,80,90,70,100,50,50,50,80,70,80,40,40,60,70,50,30];

%找出最近配送点
for i=1:31
    distance(i,:)=dist(city_coordinate(i,:),city_coordinate(individual,:)');
end

[a,b]=min(distance');

%计算费用
for i=1:31  
    expense(i)=carge(i)*a(i);
end

%距离大于3000取一个惩罚值

fit=sum(expense) + 4.0e+4*length(find(a>3000));


end