一般情况下不看MSE,只有在出错的时候再去翻MSE的值是不是正常。
[H_Data_Pilot_1] = PUCCH_ChannelEstimation(CE_Mode_DMRS,Fading_Weight,Mean_sigma_1,Mean_Pilot_1,format);%信道估计
[H_Data_Pilot_2] = PUCCH_ChannelEstimation(CE_Mode_DMRS,Fading_Weight,Mean_sigma_2,Mean_Pilot_2,format);%信道估计
%算mse
cha=abs(H_Data_Pilot_2-H_mean_ideal).^2;
chamean=mean(cha(:));
SystemParam.mse=SystemParam.mse+chamean;
仿真过程遇到跳频和不跳频产生性能差异,不知道如何分析,可以通过看MSE。
性能越好,应该MSE越小,每种情况跑500帧,信道估计的方式一样,没有问题,源于信道估计和用的信道有关。同时信道的特征也可能导致信道估计的不准。比如信道的变化不大,可能出来的效果很好,要是变化剧烈,信道估计的效果没有特别好。
看跳频和不跳频的信道估计MSE是为了去看信道的特征。跳频的与否带来的信道估计误差也会有差异。问题在于信道本身的特征
- MSE在零点1以下比较正常
- 求MSE的时候,要除帧数。仿真的时候不除的话,最后统计也要手动除,是一样的。算MSE是以单帧为单位的,准确来说是每RE为单位。
- MSE的计算差不多在500帧的时候就比较准确了。
一般信道之间相关性越强,信道估计越准确
因为信道变化越剧烈,信道估计的效果越差。比如1RB的信道估计,有两列导频,15KHz的信道估计比30khz的信道估计要更好,可以从这个角度去理解,15KHz信道之间相关性强,变化更平缓,所以信道估计更准确。
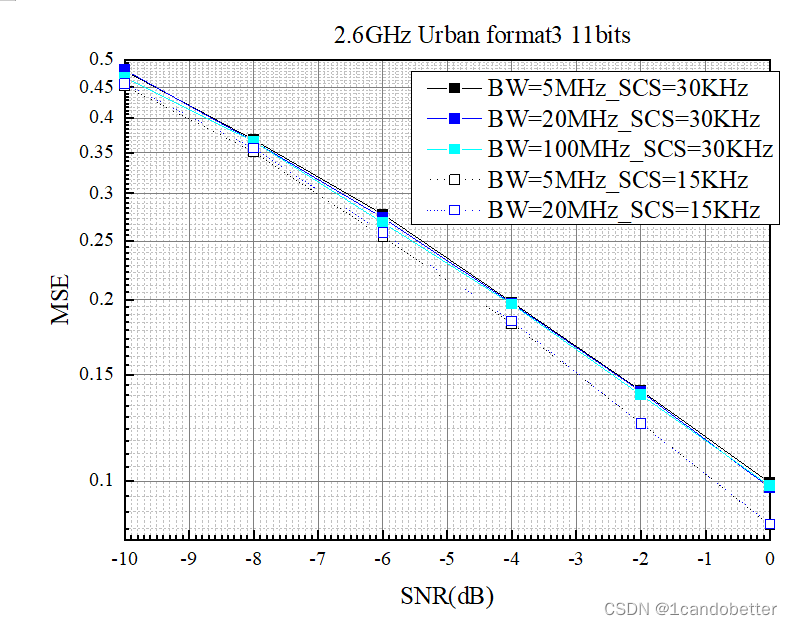





 本文探讨在MATLAB仿真中使用MSE(均方误差)指标来分析跳频和不跳频场景下信道估计的性能差异。性能良好的信道通常表现为较小的MSE,且当MSE低于0.1时被认为是正常的。MSE计算需除以帧数,500帧后数据通常能提供准确的MSE值。信道的相关性影响估计准确性,变化剧烈的信道会导致较差的估计效果。例如,15KHz信道估计通常优于30KHz,因其相关性强,变化更平缓。
本文探讨在MATLAB仿真中使用MSE(均方误差)指标来分析跳频和不跳频场景下信道估计的性能差异。性能良好的信道通常表现为较小的MSE,且当MSE低于0.1时被认为是正常的。MSE计算需除以帧数,500帧后数据通常能提供准确的MSE值。信道的相关性影响估计准确性,变化剧烈的信道会导致较差的估计效果。例如,15KHz信道估计通常优于30KHz,因其相关性强,变化更平缓。
















 2788
2788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








