题目

思路
按部就班
然后用数组T保存 t 的多项式的系数,再计算每一项然后累加
精度要求只需要delta(t) < 0.5*10**( - 小数点位数),即可
代码
import numpy as np
# 5.9
xs = [2.4, 2.5, 2.6]
ys = [[ '*' for i in range(len(xs)) ] for j in range(len(xs))]
ys[0] = [0.0025, -0.0484, -0.0968]
# ys 每行就是行序号阶的差分
# 差分
def chf(y):
l = len(xs)
for i in range( 1 , l ):
for j in range( 0 , l-i ):
# print("i,j:",i,',',j,)
y[i][j] = y[i-1][j+1] - y[i-1][j]
def jiech(n):
ans = 1
for i in range(1, n+1):
ans *= i
return ans
def cal_T(c):
T[0] = ( c-ys[0][0] ) / ys[1][0]
for i in range(1, len(xs)-1):
temp = ys[i+1][0] / ( jiech(i+1) * ys[1][0] )
T[i] = temp
print(" T :", T)
def cal_t(lim):
yu = 999
t[0] = T[0]
i = 1
while( yu >= lim ):
tsum = T[0]
temp = t[i-1]
for j in range(1, len(T)):
for k in range(1, len(T)):
temp *= (temp - k)
tsum -= temp * T[j]
t.append( tsum )
yu = abs(t[i] - t[i-1])
print(" delta t : ", yu)
i += 1
print(" t : ", t)
# 正插xs,反插ys
def main():
chf(ys)
for i in range(len(ys[0])):
print(ys[i])
print("差分表:\n", np.transpose(ys))
# C = eval(input("输入C:"))
C = 0
global T,t
T = ['*'] * (len(xs) - 1)
t = [0]
cal_T(C)
cal_t(0.0005)
h = xs[1] - xs[0]
ans = xs[0] + t[-1] * h
print(" 结果 x 约等于 => ", ans)
main()
运行结果
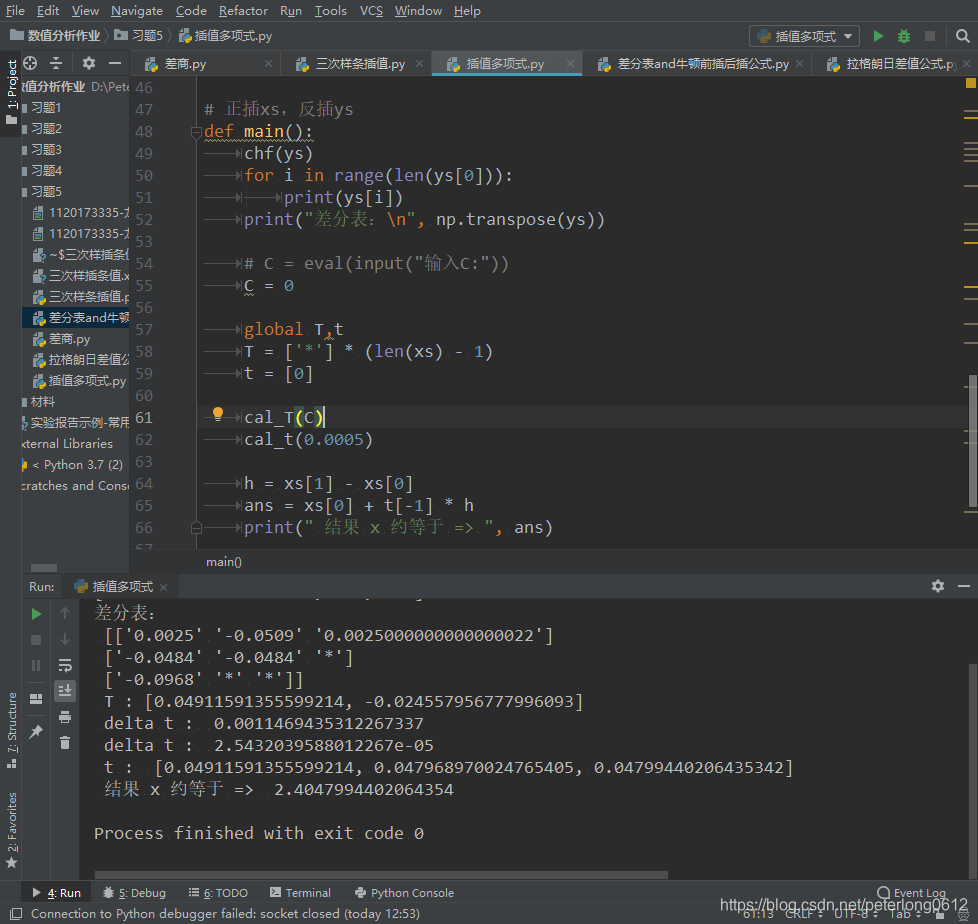





 本文介绍了一种使用多项式插值进行数值计算的方法,通过构建差分表并利用正插法和反插法计算未知点的值,实现对复杂函数的逼近。代码示例展示了如何使用Python实现这一过程,包括计算精度的控制。
本文介绍了一种使用多项式插值进行数值计算的方法,通过构建差分表并利用正插法和反插法计算未知点的值,实现对复杂函数的逼近。代码示例展示了如何使用Python实现这一过程,包括计算精度的控制。
















 4379
4379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








