题目
5.分别用迭代法、牛顿法、双点弦截法(x0=2, x1=1.9)求方程x3-3x-1=0在x=2附近的根
思路
回去看PPT
代码
# 迭代法、牛顿法、双点弦截法
# 题目:求x^3-3*x-1=0在x=2附近的根,双点弦截法(x0=2,x1=1.9)
import math
import sympy as sp
def fun(x):
return pow(x,3) - 3*x - 1;
def DiedaiIteration(x):
# 迭代公式
# sqrt()
# pow(x, 1/3)
return ( 1 + 3*x ) ** (1./3)
def diedai(p):
# 判断收敛
# 迭代公式一阶导
judge = abs( ( 1 + 3*p )**(-2./3) )
print(f"|φ'x| = {judge}")
if(judge < 1 ):
cha = 99999
i = 0
print(f"x{i} = {p}")
x1 = p
x2 = DiedaiIteration(x1)
cha = abs( x2 - x1 )
print(f"x{i+1} = {x2:06f}, 差cha = {cha:06f}")
while(cha > 0.00001):
x1 = x2
x2 = DiedaiIteration(x2)
cha = abs( x2 - x1 )
i += 1
print(f"x{i+1} = {x2:06f}, 差cha = {cha:06f}")
else:
print("迭代公式一阶导|x=({p}) >= 1,不确定收敛性")
def NewtonIterat(x):
# 牛顿迭代公式:x(n+1) = xn-(f(xn)/f'(xn))
# 公式不简化
# return x - (fun(x) / ( 3 * x**2 - 3 ))
# 公式简化
return (2 * x**3 + 1) / ( 3 * ( x**2 - 1 ) )
def newton(p):
# 1 形成迭代公式 NewtonIterat()
# 2 确定初值:
# 在[a,b]满足 f(a)f(b)<0 有根 && f'(x)!=0根唯一 && f(x)f''(x) > 0 不变号,则迭代收敛
# fun(x0)*6*x0 =12 > 0
# 3 迭代
cha = 99999
x = p
i = 0
print(f"x{i} = {x:6f}")
while(cha > 1e-5):
temp = NewtonIterat(x)
cha = abs( temp - x )
x = temp
i += 1
print(f"x{i} = {x:6f}, 差cha = {cha:6f}")
def XianjieIterat(x1,x2):
return ( x1*fun(x2) - x2*fun(x1) ) / ( fun(x2) - fun(x1) )
def xianjie(p1,p2):
# 1 f(a)f(b) < 0 && f'(x) != 0 ,对任意x0,x1 ∈ [a,b] 收敛
# 2 迭代 x(n+1) = ( x(n-1)*f(xn) - xn*f(x(n-1)) ) / (f(xn) - f(x(n-1)) )
x1,x2 = p1,p2
f1,f2 = fun(x1),fun(x2)
cha = 999
i = 0
print(f"x{i} = {x1:6f}, f(x{i}) = {f1:6f}")
i += 1
print(f"x{i} = {x2:6f}, f(x{i}) = {f2:6f}")
while(cha > 1e-6 ):
x = XianjieIterat(x1,x2)
f = fun(x)
cha = abs(x-x2)
x1 = x2
x2 = x
i += 1
print(f"x{i} = {x:6f}, f(x{i}) = {f:6f}, 差cha = {cha:6f} ")
return
def main():
p = 2.0
print("---------迭代法--------")
diedai(p)
print("---------牛顿法--------")
newton(p)
print("---------双点弦截法--------")
p1,p2 = 1.9, 2.0
xianjie(p1,p2)
main()
效果:
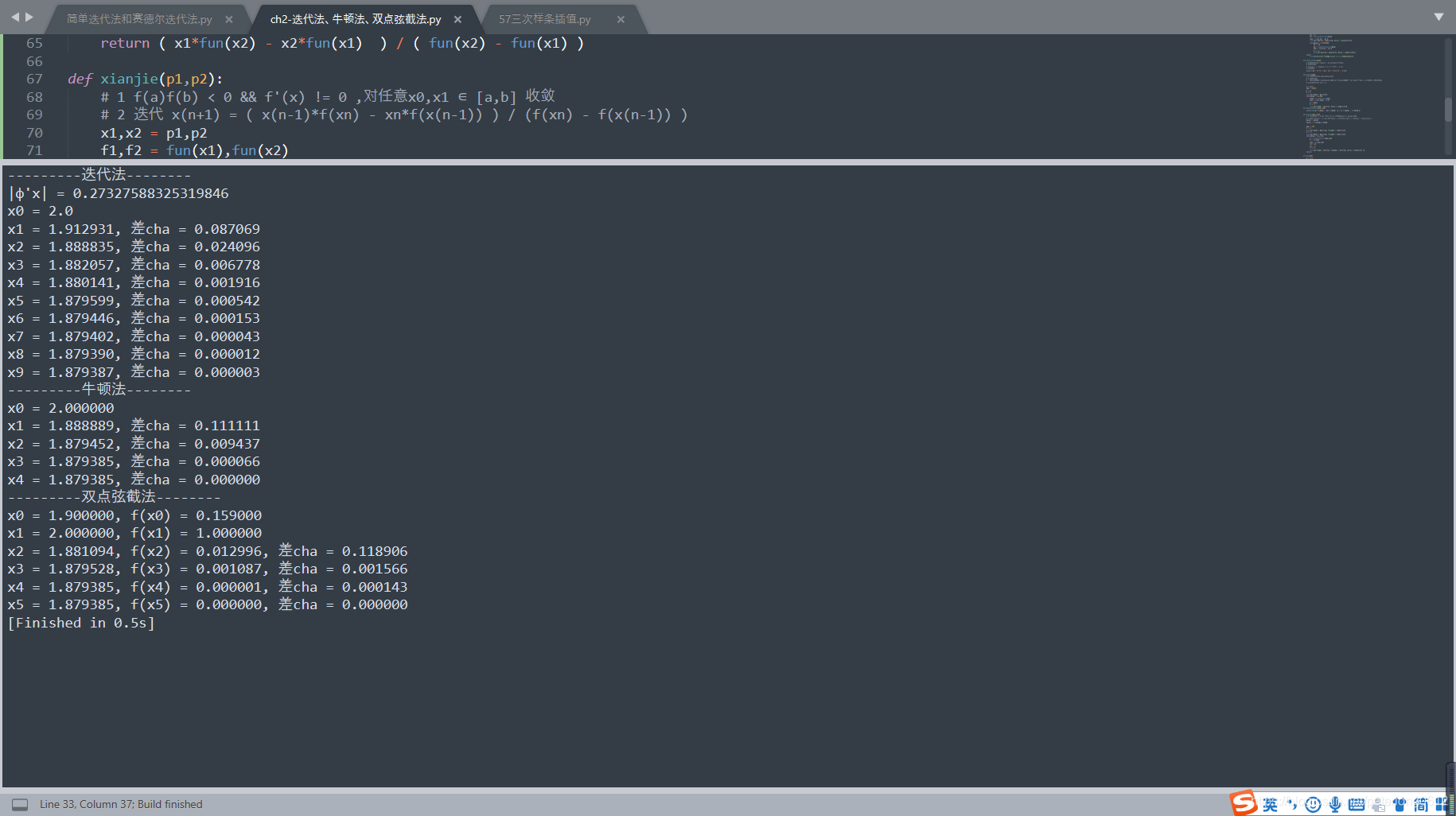





 本文详细介绍了使用迭代法、牛顿法及双点弦截法求解方程x³-3x-1=0在x=2附近根的具体过程。通过Python编程实现了三种方法,并展示了每种方法的收敛情况,为数值分析的学习者提供了实用的参考。
本文详细介绍了使用迭代法、牛顿法及双点弦截法求解方程x³-3x-1=0在x=2附近根的具体过程。通过Python编程实现了三种方法,并展示了每种方法的收敛情况,为数值分析的学习者提供了实用的参考。
















 4540
4540

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








