CS224n 深度自然语言处理(四) Note - Backpropagation and computation graphs

本文为笔者学习CS224N所做笔记，所包含内容不限于课程课件和讲义，还包括笔者对机器学习、神经网络的一些理解。所写内容难免有难以理解的地方，甚至可能有错误。如您在阅读中有疑惑或者建议，还望留言指正。笔者不胜感激！

在本章中，将着重讨论以下内容：

1. 如何更新神经网络参数？
2. 以何种形式保存更新结构？
3. 搭建和训练神经网络的技巧.

梯度和导数

上一章提到，应该最小化损失函数。损失函数的参数是神经网络参数，由于梯度的方向是函数上升最快的方向，故若想最小化损失函数，应该按负梯度方向更新参数，即梯度下降。而为了求解损失函数对参数的梯度，就涉及到了微分的问题。

梯度计算

对于上一章提出的简单的神经网络分类器，有如下的形式：

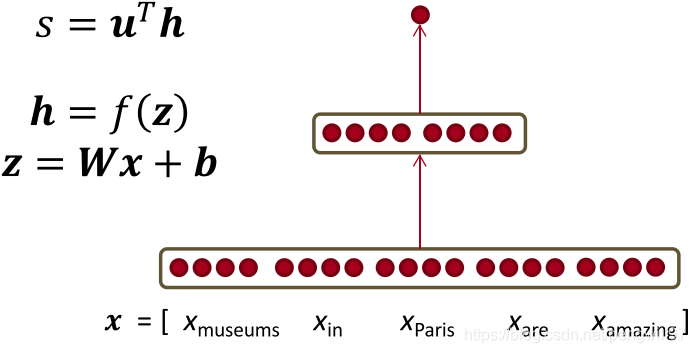
现在计算$\frac{\partial s}{\partial W}$，根据链式法则，有
$$\frac{\partial s}{\partial W}=\frac{\partial s}{\partial h}\cdot \frac{\partial h}{\partial z}\cdot \frac{\partial z}{\partial W}$$
此处$s,W,h,z$均为矩阵或者向量的形式，涉及到矩阵求导，较为繁琐。为了简单清楚的阐述其原理，我们求对于$W$中某个特定元素的求导规则，即计算$\frac{\partial s}{\partial W_{ij}}$。同时，我们神经网络用图的方式更加详细的表示出来。

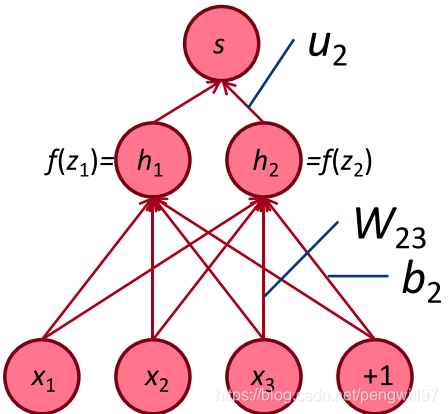
再做一个简化，令$\frac{\partial s}{\partial W}$链式法则展开的前两项为$\delta$，关注$\frac{\partial z}{\partial W}$,即
$$\partial <$$