【模糊PI控制（从原理到simulink仿真到C代码实现）】

1. 模糊控制的基础知识

1.1 模糊PI控制理论想法（有基础直接看第2点以后）

PI控制是根据误差进行调节，利用比例Kp与积分KI实现反馈调节。但传统PI控制固定比例系数Kp与积分系数KI不是我们想要的，我们按照经验想：

1. E误差较大时 ，将Kp系数增大，达到更快的调节，缩小调节时间；
2. EC误差变化率较大时 ，将Ki系数减小，减小误差积分，使系统减小积分饱和；

所以模糊PI控制就是来实时控制改变Kp与Ki，由E误差及EC误差变化率来控制输出detal_Kp和detal_Ki;得到最终PI控制系数

Kp = Critical_Kp + detal_Kp Ki = Critical_Ki + detal_Ki

解释：Critical_Kp 、Critical_Ki 为原来采用PI控制的临界值，detal_Kp 、detal_Ki为模糊控制器修改的P、I增量，Kp 、Ki为最总PI控制器的比例与积分系数。如下图以模糊PI控制cuk变换器电压的例子：

1.2 模糊控制基础理论

模糊控制器又称FC控制器，是FC控制系统与其他各类控制系统的最大区别，是模糊控制系统的核心.
如图4-1 所示，按照输入的维数划分，模糊控制器结构可以分为3类。

1. 一维FC控制器，其输入变量 x 仅有偏差 e 一项，对动态偏差调节品质较差。
2. 二维 FC 控制器，x 有偏差 e 和偏差的变化率 ec 两个分量，偏差的变化率可以反应受控过程中输出变量的动态特性，在控制效果上比一维 FC 更具优势，是目前采用最多的一类FC 结构。
3. 三维 FC 控制器增加了变化率的变化率 ecc 分量，从原理上讲，三维FC的动静态特性要优于二维 FC，但实际上，即使三维的 FC 也不可消除静态误差，且由于维数增高产生的模糊子集数要大大多于所实现的动态特性，随着维数的增多，系统的控制性能越优良，但造成代价就是控制规则数目大大增加和模糊推理运算量急剧增加。因此三维的 FC 只适用于一些特殊的场合。
4. 结论：由于最基本二维FC控制器结构简单、原理清晰、应用广泛。

一个完整的二维 FC模糊控制过程包括：模糊化过程、模糊化推理过程和清晰化过程。

1. 模糊化：将精确地输入量转换为模糊推理中使用的模糊量。
2. 模糊推理：将通过模糊化转换后的系统模糊输入量进行模糊推理，模糊推理输出也为模糊量。模糊推理由模糊规则确定。
3. 清晰化：将模糊推理过程得到的模糊量进行清晰化处理得到可以被被控对象使用的清晰量。

1.2.1 量化因子与比例因子概念

量化因子：就是输入量归一化到一个范围的因子，打个比方，如果是让你设计一个模糊控制器，你的标准输入是限制在[-3,3]之间，但是你现在实际输入却是在[-300,300]之间，你如何处理？最简单办法就是将 实际输入/100 作为标准输入 给到模糊控制器标准输入，1/100就是你的量化因子。当然这1/100是线性量化，如果你要做一个非线性量化因子也可以。

比例因子：就是输出标准量放大到你实际需要的因子，打个比方，如果是让你设计一个模糊控制器，你的标准输出是限制在[-3,3]之间，但你实际需要的输出却是在[-30,30]之间，你如何处理？最简单办法就是将 标准输出*10 作为实际输出，10就是你的比例因子。

总体关系如下图：

1.2.2 模糊控制器的论域与隶属函数概念

从上文不难发觉到，论域是我们规定一个输入或输出标准范围，所有输入或输出都必须规定在其中范围，那论域的作用是用来干什么的？体现在哪里？隶属函数又有啥作用？我们来看下面这张图。

图中：[0 100]为论域，有三条隶属度曲线S（0-40-100），M（0-10-50-90-100），L（0-60-100）

如果给你输入为20，你是不是能轻易得到与[S，M，L]曲线分别交点为[0.5、0.25、0.0]
如果给你输入为50，你是不是能轻易得到与[S，M，L]曲线分别交点为[0.0、1.00、0.0]
如果给你输入为80，你是不是能轻易得到与[S，M，L]曲线分别交点为[0.0、0.25、0.5]
其实S、M、L分别代表小、中、大，你输出得到0-1之间的比值，为他们各种占比，以输入20为例，你得到S小的隶属度占50%，M中隶属度为25%，L大隶属度为0%，这个操作也就是模糊化处理

那如果给你一个输入110或者-10，你能得到什么？会出现错误，因为三条隶属度就只规定了0-100的区间，这就是你要规划的论域。

上面只是一个三条三角隶属度例子，理论你可以随意规划论域大小，规划N条隶属度，隶属度形式也可以多种多样，如下图：
这是一个论域在[-3 3]之间，有七条隶属函数[NB、NM、NS、ZE、PS、PM、PB]，代表{负大、负中、负小、零、正小、正中、正大}。

当然有输入隶属度，输入论域，当然也有输出的论域，输出隶属度，其本质跟输入类似，但是它就不是按一个输入得到一组隶属度数据，也不是简单反向操作由一组隶属度得到一个输出值，具体后面在1.2.4点再说明

1.2.3 模糊规制表概念与模糊推理概念

上一点我们也可以又一个输入模糊化成一组数据占各自隶属度大小，那该如何利用这组数据，就得利用到模糊规则表，下面我们来看一个简单的（二输入一输出）模糊规则表：

二输入一输出系统模型：

模糊控制规则表

假设输入oil=20%：mud=80%
输入到oil隶属函数曲线可以得到：当oid=20%，与[S，M，L]曲线分别交点为[0.5、0.25、0.0]；
输入到mud隶属函数曲线可以得到：当mud=80%，与[S，M，L]曲线分别交点为[0.0、0.25、0.5]；
此时：【oil激活S、M】，【mud激活M、L】，对应规则表激活四条规则
分别是：
oil含油量少（oil：S[0.5]），mud含泥量中（mud：M[0.25]），time洗涤时间少（time：S[0.25]]）
oil含油量少（oil：S[0.5]]），mud含泥量多（mud：L[0.5]），time洗涤时间中（time：M[0.5]]）
oil含油量中（oil：M[0.25]]），mud含泥量中（mud：M[0.25]），time洗涤时间中（time：M[0.25]）
oil含油量中（oil：M[0.25]），mud含泥量多（mud：L[0.5]]），time洗涤时间中长（time：ML[0.25]）
可以看出：time激化比例是两者最小决定的。

哪激化洗涤时间有三种：time：【S，M，ML】，这就是模糊控制规则表作用，哪最终洗涤时间是多少？你想想得采用什么方式才能将激活time：【S，M，ML】变成一个数字时间输出，这类做法叫做清晰化/解模糊。

1.2.4 清晰化/解模糊的概念与方式

这里是个关键点，如何把前面模糊规则表规则变化成一个具体标准数值。模糊控制清晰化输出量的判决方式有常见的三种：最大隶属度法、面积中心法（即重心法）和加权平均法：

• 最大隶属度法
• 面积中心法（即重心法）
• 加权平均法

实际工程应用最长见的就是采用面积中心法，其他两种方式感兴趣的可以网上搜搜一大堆解释。下面我们来详细介绍什么是面积中心法：
面积中心法顾名思义就是，寻找一个面积的质点，下面我们直接上图，根据假设输入oil=20%：mud=80%，规则表，隶属度按上一例子讲的哪有，如何解模糊化。

当输入oil=20%：mud=80%只激化图中第（2，3，5，6）条对应着激化四条规则
第2规则：oil含油量少（oil：S[0.5]），mud含泥量中（mud：M[0.25]），time洗涤时间少（time：S[0.25]]）
第3规则：oil含油量少（oil：S[0.5]]），mud含泥量多（mud：L[0.5]），time洗涤时间中（time：M[0.5]]）
第5规则：oil含油量中（oil：M[0.25]]），mud含泥量中（mud：M[0.25]），time洗涤时间中（time：M[0.25]）
第6规则：oil含油量中（oil：M[0.25]），mud含泥量多（mud：L[0.5]]），time洗涤时间中长（time：ML[0.25]）
注意看time的面子是怎么来的？其实就是每个激化隶属曲线与激化隶属度大小相交的面积！！！！
例如第2规则，time激化隶属度是S[0.25]，就是S隶属函数曲线与直线x=0.25先交以下的面积大小
最后如何得到time=29.9呢？就是激活四个面积区域相或面积，求该面积质点就是模糊要输出的值。

1.2.5 基于污泥油量的模糊控制洗衣机例子，搞懂他的控制流程

B站有位老师讲的非常不错，20分钟左右，大家可以看一下：模糊洗衣机控制系统: link
看完也能对上面所学进行一次复习，虽然这例子不是模糊PI空载原理，但模糊控制原理主要原理都是相似的，可以帮你更好了解什么是模糊控制，了解整个控制流程，对你设计模糊控制器很有帮助。

2 模糊PI控制原理设计

默认前面全部学会了，直接给图了

2.1 模糊PI整体框架

2.1 模糊PI隶属函数、量化因子、比例因子

本文中模糊控制为双输入双输出结构，假定输入误差的变化范围为[e_min,e_max]，输入误差变化率的变化范围为[ec_min,ec_max]，模糊控制器输出分别为△K_p和△K_i。设误差论域范围选取[e_min*， e_max*]， 误差变化率论域范围选取[ec_min*， ec_max*]， △K_p和△K_i论域也分别设置为[K_pmin*， K_pmax*] 与[K_imin*， K_imax*]，表示可以在初始参数点上下调节。由此可以确定量化因子和比例因子系数为：

实验中输入考虑在正负范围内对称，所以误差论域范围选取[-3，3]，误差变化率论域范围选取[-3，3]。输出也考虑到正负变化，所以△K_p和△K_i论域也设置为[-3，3]，表示可以在初始参数点上下调节。

根据工程实际情况，输入变量e和ec的模糊子集为{负大，负中，负小，零，正小，正中，正大}，记为{NB，NM，NS，ZE，PS，PM，PB}，将偏差e和偏差变化率ec量化到{-3,3}论域范围（其他范围都可以）。同时，输出变量△K_p和△K_i的模糊子集{负大，负中，负小，零，正小，正中，正大}，记为{NB，NM，NS，ZE，PS，PM，PB}，分别量化到{-3,3}的论域内，其隶属函数曲线分别如下图所示。

e、ec、△K_p和△K_i隶属函数曲线

2.1 Kp与△Ki模糊控制规则表

原理：当e误差在最大值时候，需要将后续Kp比例系数增加，减少误差，而Kp增加时候需要将Ki积分系数减少，减少积分饱和同时增加系统稳定性。当ec误差变化率最大时候，需要将Ki积分系数减少，减少积分饱和，同时增加比例系数Kp。

根据各模糊子集的隶属度赋值表和各参数的模糊控制模型，应用模糊合成推理设计PI参数模糊矩阵表，模糊控制器将清晰化得到结果与比例因子相乘以后，输出△K_p和△K_i对PI参数进行整定。 其计算公式如下：

K_p=K_p0+△K_p，K_i=K_i0+△K_i

其中，K_p0与K_i0为常用常规PI控制器选取的参数，K_p与K_i为整定后的参数。

3 matlab的simulink仿真

3.1 simulik的仿真模型搭建

这一步很简单，matlab的simulink有专门的工具可以用来实现，现在我们来根据前面说的第二大点来做simulink仿真。下图为总体框架

3.1.1 模糊控制部分

fuzzy内部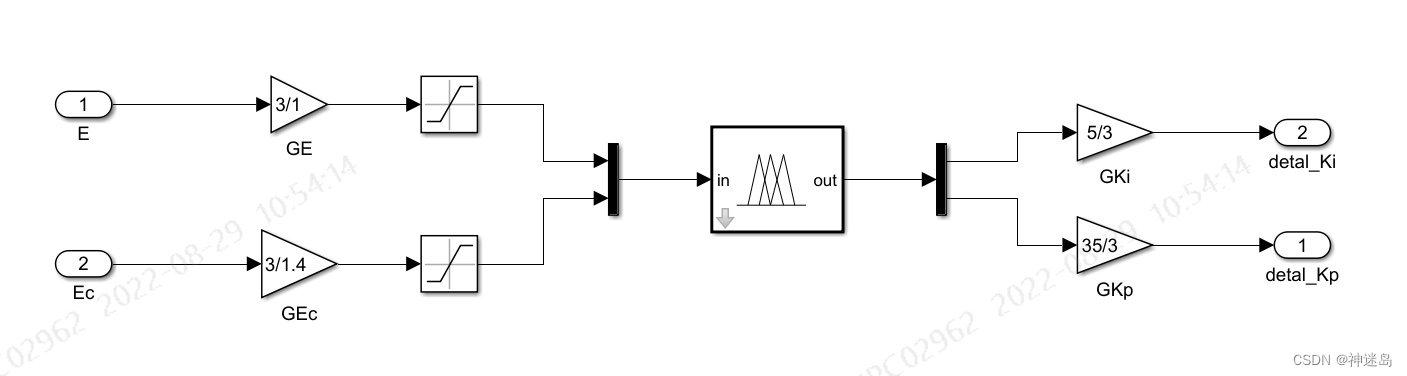输入：E为误差，Ec为误差变化率，输出：detal_Kp为△KP，detal_Ki为△Ki; 中间： GE、GEc为误差和误差变化率的量化因子，GKP，GKi为detal_Kp和detal_Ki的比例因子

3.1.2 模糊控制部分PI控制部分

输入：E为误差，Critical_KP为PI临界比例系数，Critical_KI为临界积分系数；
输出：U为PI控制输出；
中间：detal_Kp和detal_Ki为上图模糊输出△Kp与△Ki;

3.2 设计模糊控制的控制器

在命令行直接输入：fuzzy
系统会打开模糊控制器设计页面

3.2.1 输入及输出个数设计

按下面操作生产两输入两输出结构

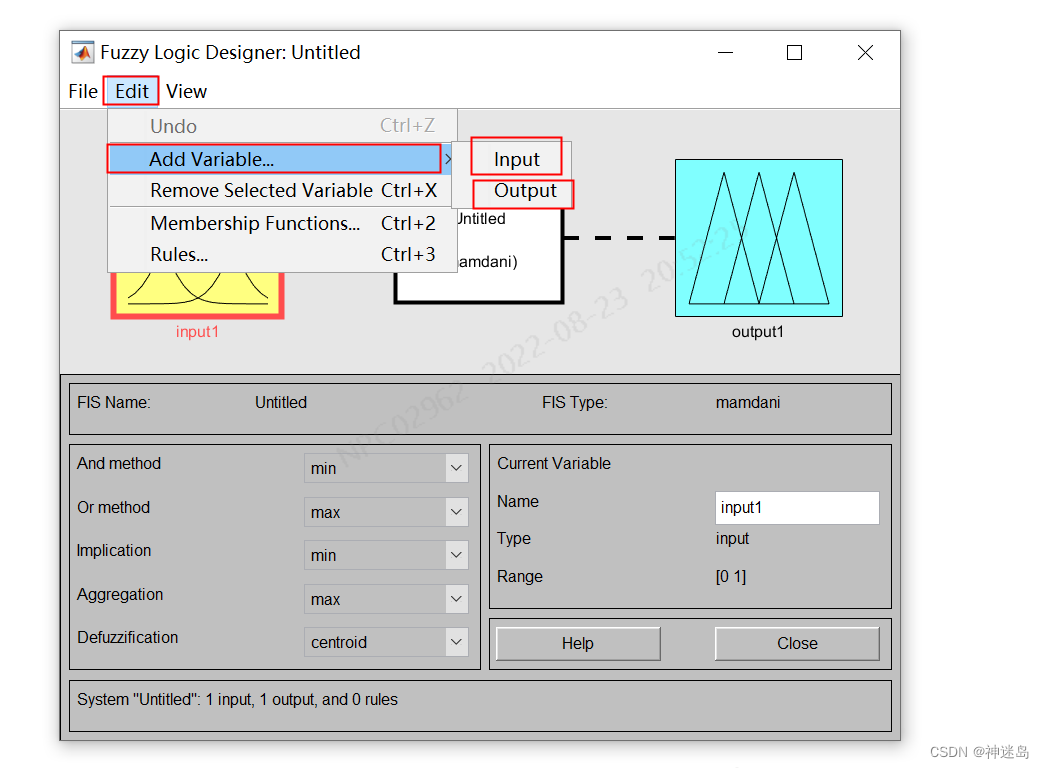
最终结构

3.2.2 论域及隶属函数设计

点开一个

最总呈现：2.1 模糊PI隶属函数、量化因子、比例因子中四个隶属曲线图一致

3.2.3 编写模糊控制规则表

按照：2.1 Kp与△Ki模糊控制规则表添加49条规则，具体部分如图下显示：注意他们关系是：if E is XX EC is XX then Kp is XX and Ki is XX

搞定保存后，当前matlab的工作目录下有一个：xxx.fis ，我这里因为名字起来fuzzy_PI，所以才会是fuzzy_PI.fis

3.2.4 编写模糊控制文件与simulink挂钩

3.3 模糊PI控制的整体小例子（免费资源）

整体框架

实验对比

明显可以看出fuzzy_PI比PI，反应时间更加快速，基本无超调量
资源：链接：https://download.youkuaiyun.com/download/pengrunxin/86502151 : link，[matlab版本2018A],低于这个版本自己解决

4.模糊PI控制C语言代码实现

走到这一步，模糊PI控制原理跟流程都很熟悉了，根据自己想法写一个模糊控制器相对来说也很容易。我们只要完成模糊PI的模糊控制器部分代码，PI控制部分代码网上很多版本。

4.1 simulik模糊控制PI的C代码导出

simulink直接导出c语言是最方便快捷的方案，可是代码可阅读性就够呛。
1.将模糊PI控制部分单独拎出来一个工程，像这样：

2.设置一下





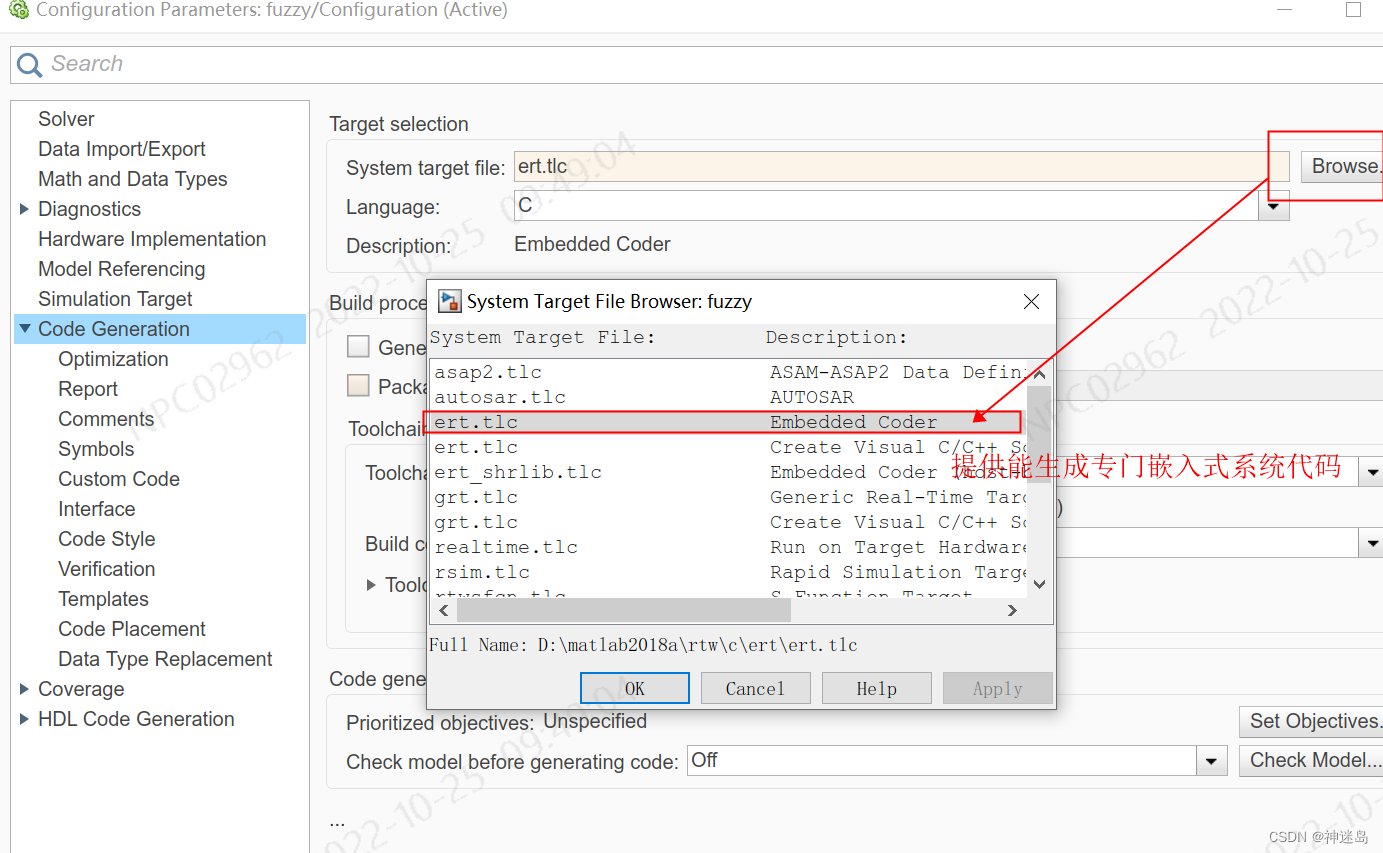
点击生成代码，其他都是默认，只有这里根据你代码运行的设备进行选择，我是在64位的windows系统上测试，运行环系是VS2010.

完成后，当前目录下有一个：xxxxxx_ert_rtw文件夹，因为我的simulink的文件是fuzzy2.slx，我在当前目录会生成fuzzy2_ert_rtw文件夹，如下：

这里我也放一份我自己编译出来的代码资料：链接: fuzzy2_ert_rtw：待定

4.2 simulink代码解读

函数入口在 ert_main.c中的 rt_OneStep()函数中，你按这个流程去看一遍就知道代码在做什么了

我们自己写个main测一下，先将上图intT main（int argc， const char* argv[ ]）函数注释掉，直接在fuzzy2.c最后添加下面代码，编译运行。

#include <stddef.h>
const ConstP rtConstP = {
  /* Expression: fis.outputSamplePoints
   * Referenced by: '<S1>/Output Sample Points'
   */
  { -3.0, -3.0, -2.94, -2.94, -2.88, -2.88, -2.82, -2.82, -2.76, -2.76, -2.7,
    -2.7, -2.64, -2.64, -2.58, -2.58, -2.52, -2.52, -2.46, -2.46, -2.4, -2.4,
    -2.34, -2.34, -2.2800000000000002, -2.2800000000000002, -2.2199999999999998,
    -2.2199999999999998, -2.16, -2.16, -2.1, -2.1, -2.04, -2.04, -1.98, -1.98,
    -1.92, -1.92, -1.86, -1.86, -1.8, -1.8, -1.74, -1.74, -1.68, -1.68, -1.62,
    -1.62, -1.56, -1.56, -1.5, -1.5, -1.44, -1.44, -1.38, -1.38, -1.32, -1.32,
    -1.26, -1.26, -1.2, -1.2, -1.14, -1.14, -1.08, -1.08, -1.02, -1.02, -0.96,
    -0.96, -0.89999999999999991, -0.89999999999999991, -0.83999999999999986,
    -0.83999999999999986, -0.7799999999999998, -0.7799999999999998,
    -0.7200000000000002, -0.7200000000000002, -0.66000000000000014,
    -0.66000000000000014, -0.60000000000000009, -0.60000000000000009, -0.54,
    -0.54, -0.48, -0.48, -0.41999999999999993, -0.41999999999999993,
    -0.35999999999999988, -0.35999999999999988, -0.29999999999999982,
    -0.29999999999999982, -0.24000000000000021, -0.24000000000000021,
    -0.18000000000000016, -0.18000000000000016, -0.12000000000000011,
    -0.12000000000000011, -0.060000000000000053, -0.060000000000000053, 0.0, 0.0,
    0.060000000000000053, 0.060000000000000053, 0.12000000000000011,
    0.12000000000000011, 0.18000000000000016, 0.18000000000000016,
    0.24000000000000021, 0.24000000000000021, 0.29999999999999982,
    0.29999999999999982, 0.35999999999999988, 0.35999999999999988,
    0.41999999999999993, 0.41999999999999993, 0.48, 0.48, 0.54, 0.54,
    0.60000000000000009, 0.60000000000000009, 0.66000000000000014,
    0.66000000000000014, 0.7200000000000002, 0.7200000000000002,
    0.7799999999999998, 0.7799999999999998, 0.83999999999999986,
    0.83999999999999986, 0.89999999999999991, 0.89999999999999991, 0.96, 0.96,
    1.0199999999999996, 1.0199999999999996, 1.08, 1.08, 1.1399999999999997,
    1.1399999999999997, 1.2000000000000002, 1.2000000000000002,
    1.2599999999999998, 1.2599999999999998, 1.3200000000000003,
    1.3200000000000003, 1.38, 1.38, 1.4400000000000004, 1.4400000000000004, 1.5,
    1.5, 1.5599999999999996, 1.5599999999999996, 1.62, 1.62, 1.6799999999999997,
    1.6799999999999997, 1.7400000000000002, 1.7400000000000002,
    1.7999999999999998, 1.7999999999999998, 1.8600000000000003,
    1.8600000000000003, 1.92, 1.92, 1.9800000000000004, 1.9800000000000004, 2.04,
    2.04, 2.0999999999999996, 2.0999999999999996, 2.16, 2.16, 2.2199999999999998,
    2.2199999999999998, 2.2800000000000002, 2.2800000000000002, 2.34, 2.34,
    2.4000000000000004, 2.4000000000000004, 2.46, 2.46, 2.5199999999999996,
    2.5199999999999996, 2.58, 2.58, 2.6399999999999997, 2.6399999999999997, 2.7,
    2.7, 2.76, 2.76, 2.8200000000000003, 2.8200000000000003, 2.88, 2.88,
    2.9400000000000004, 2.9400000000000004, 3.0, 3.0 }
};

int_T main(int_T argc, const char *argv[])
{
  /* Unused arguments */
  (void)(argc);
  (void)(argv);

	//输入结构体rtU;输出结构体rtY;一步模糊控制函数fuzzy2_step();
  rtU.E=2.0;
  rtU.Ec=2.0;
  fuzzy2_step();
  printf("when E=%f,Ec=%f,result Kp=%f ki=%f",rtU.E,rtU.Ec,rtY.detal_Kp,rtY.detal_Ki);

  /* Disable rt_OneStep() here */
  return 0;
}

代码运行结果：when E=2.000000,Ec=2.000000,result Kp=-2.003539 ki=2.679194，到这里想怎么用就可以怎么用了。

4.3 编写自己模糊PI控制代码

上文已经能自己设计模糊控制器了，并输出代码，但这个可读性真的太差了，改个什么都麻烦，运行速度也太难了，所以我想自己参考matlab思路，自己手撕一个模糊控制器，前期就可读性高一点，后期再弄些可通用性。
下面是我第一版本代码，加了注释，看一下你们就知道了。
< fuzzy.h>

/*
 * File: fuzzy.h
 *
 * Code generated for Simulink model 'fuzzy',Modify and organize the code.
 *
 * Model version                  : 1.1
 * Simulink Coder version         : 9.5 (R2021a) 14-Nov-2020
 * C/C++ source code generated on : Fri May 27 17:07:58 2022
 * Modified by                    : Shengmidao
 *
 * Target selection: ert.tlc
 * Embedded hardware selection: Intel->x86-64 (Windows64)
 * Code generation objectives: Unspecified
 * Validation result: Not run
 */

#ifndef FUZZY_H_
#define FUZZY_H_
#include <math.h>
#include <string.h>


//1：fuzzy：模糊控制部分
/*定义采集[-3,3]论语，一共101个点*/
const double fuzzy_ConstP[101] = {
    -3.0, -2.94, -2.88, -2.82, -2.76,-2.6999999999999997, -2.6399999999999997, -2.58, -2.52, -2.46, -2.4,
    -2.34, -2.28, -2.2199999999999998, -2.16,-2.1, -2.04, -1.98, -1.92,-1.8599999999999999, -1.7999999999999998,
    -1.74, -1.68, -1.6199999999999999, -1.56, -1.5, -1.44, -1.38, -1.3199999999999998, -1.26, -1.2, -1.14,
    -1.08, -1.02, -0.96,  -0.89999999999999991, -0.84, -0.78, -0.72,-0.65999999999999992, -0.6, -0.54, -0.48,
    -0.42, -0.36, -0.3, -0.24, -0.18, -0.12, -0.06, 0.0, 0.06, 0.12, 0.18, 0.24, 0.3, 0.36, 0.42, 0.48,  0.54, 0.6,
    0.65999999999999992, 0.72, 0.78, 0.84, 0.89999999999999991, 0.96, 1.02, 1.08, 1.14, 1.2,1.26, 1.3199999999999998,
    1.38, 1.44, 1.5, 1.56, 1.6199999999999999, 1.68, 1.74,1.7999999999999998, 1.8599999999999999,
    1.92, 1.98, 2.04, 2.1, 2.16,2.2199999999999998, 2.28, 2.34, 2.4,2.46, 2.52, 2.58, 2.6399999999999997, 
    2.6999999999999997, 2.76, 2.82, 2.88,2.94, 3.0
};

/* 定义输入结构体 */
typedef struct {
  double E;                            /* '<Root>/E' */
  double Ec;                           /* '<Root>/Ec' */
} ExtU_fuzzy_T;

/* 定义输出结构体 */
typedef struct {
  double detal_Kp;                     /* '<Root>/detal_Kp' */
  double detal_Ki;                     /* '<Root>/detal_Ki' */
} ExtY_fuzzy_T;

/*模糊控制的七个隶属度，论域（-3，3）*/
#define NB (1)
#define NM (2)
#define NS (3)
#define ZO (4)
#define PS (5)
#define PM (6)
#define PB (7)

/* .Kp，Ki七条规则隶属曲线，在(-3,3)各取101个点*/
double rtb_aggregatedKp_init[707];
double rtb_aggregatedKi_init[707];

/*模糊控制规则表*/
int ruleKp[49];
int ruleKi[49];

/* 三角隶属函数 */
/*@double :量化后标准值输入*/
/*@params :三角隶属函数三个定点*/
static double fuzzy_trimf(double x, const double params[3]);

/* 模糊控制的输入隶属函数计算方程 */
/* @inputs : E、Ec输入量化值*/
/* @inputMFCache_E  : 输出E的7个的隶属度*/
/* @inputMFCache_EC : 输出EC的7个的隶属度*/
static void fuzzy_createInputMFCache(const double inputs[2], double inputMFCache_E[7],double inputMFCache_EC[7]);

/*[b c]高斯曲线输出在[-3,3]的101个点*/
static void fuz_evaluateCommonMembershipFcn(const double x[101], const double params[2],double y[101]);

/*三角函数输出在[-3,3]的101个点*/
static void fuzzy_trimf_a(const double x[101], const double params[3], double y[101]);

/* 模糊控制的一步函数*/
void fuzzy_step(ExtU_fuzzy_T *U,ExtY_fuzzy_T *Y);

/*
 * File: fuzzy.c
 *
 * The code refers to Simulink and has been modified
 *
 * Author             : shengmidao
 * Model version                  : 1.1
 * Simulink Coder version         : 9.5 (R2021a) 14-Nov-2020
 * C/C++ source code generated on : Fri May 27 17:07:58 2022
 *
 * 模糊PI控制分为两部分组成：1：fuzzy：模糊控制部分 2：PI：增量式PI控制部分
 * fuzzy: base on Simulink fuzzy
 * PI : base on Incremental pi
 */

#include "fuzzy.h"
#include <stdio.h>

///
//1：fuzzy：模糊控制部分

/* 三角隶属函数 */
/*@double :量化后标准值输入*/
/*@params :三角隶属函数三个定点*/
static double fuzzy_trimf(double x, const double params[3])     //取出量化后相对与隶属函数高度的占比值
{
  double y;
  y = 0.0;
  if ((params[0] != params[1]) && (params[0] < x) && (x < params[1])) {
    y = 1.0 / (params[1] - params[0]) * (x - params[0]);
  }

  if ((params[1] != params[2]) && (params[1] < x) && (x < params[2])) {
    y = 1.0 / (params[2] - params[1]) * (params[2] - x);
  }

  if (x == params[1]) {
    y = 1.0;            //占比最大
  }
  return y;
}

/* 模糊控制的输入隶属函数计算方程 */
/* @inputs : E、Ec输入量化值*/
/* @inputMFCache_E  : 输出E的7个的隶属度*/
/* @inputMFCache_EC : 输出EC的7个的隶属度*/
static void fuzzy_createInputMFCache(const double inputs[2], double inputMFCache_E[7],double inputMFCache_EC[7])
{
  double tmp[3];
  //计算E的隶属度
  inputMFCache_E[0] = exp(-((inputs[0] - -3.0) * (inputs[0] - -3.0)) / 0.36074018);      //NB
  tmp[0] = -3.0;
  tmp[1] = -2.0;
  tmp[2] = -1.0;
  inputMFCache_E[1] = fuzzy_trimf(inputs[0], tmp);                                       //NM
  tmp[0] = -2.0;
  tmp[1] = -1.0;
  tmp[2] = 0.0;
  inputMFCache_E[2] = fuzzy_trimf(inputs[0], tmp);                                      //NS
  tmp[0] = -1.0;
  tmp[1] = 0.0;
  tmp[2] = 1.0;
  inputMFCache_E[3] = fuzzy_trimf(inputs[0], tmp);                                      //ZO
  tmp[0] = 0.0;
  tmp[1] = 1.0;
  tmp[2] = 2.0;
  inputMFCache_E[4] = fuzzy_trimf(inputs[0], tmp);                                      //PS
  tmp[0] = 1.0;
  tmp[1] = 2.0;
  tmp[2] = 3.0;
  inputMFCache_E[5] = fuzzy_trimf(inputs[0], tmp);                                      //PM
  inputMFCache_E[6] = exp(-((inputs[0] - 3.0) * (inputs[0] - 3.0)) / 0.36193032);       //PB
  //计算Ec的隶属度
  inputMFCache_EC[0] = exp(-((inputs[1] - -3.0) * (inputs[1] - -3.0)) / 0.36074018);     //NB
  tmp[0] = -3.0;
  tmp[1] = -2.0;
  tmp[2] = -1.0;
  inputMFCache_EC[1] = fuzzy_trimf(inputs[1], tmp);                                       //NM
  tmp[0] = -2.0;
  tmp[1] = -1.0;
  tmp[2] = 0.0;
  inputMFCache_EC[2] = fuzzy_trimf(inputs[1], tmp);                                      //NS
  tmp[0] = -1.0;
  tmp[1] = 0.0;
  tmp[2] = 1.0;
  inputMFCache_EC[3] = fuzzy_trimf(inputs[1], tmp);                                      //ZO
  tmp[0] = 0.0;
  tmp[1] = 1.0;
  tmp[2] = 2.0;
  inputMFCache_EC[4] = fuzzy_trimf(inputs[1], tmp);                                      //PS
  tmp[0] = 1.0;
  tmp[1] = 2.0;
  tmp[2] = 3.0;
  inputMFCache_EC[5] = fuzzy_trimf(inputs[1], tmp);                                      //PM
  inputMFCache_EC[6] = exp(-((inputs[1] - 3.0) * (inputs[1] - 3.0)) / 0.36193032);
}

/*[b c]高斯曲线输出在[-3,3]的101个点*/
static void fuz_evaluateCommonMembershipFcn(const double x[101], const double params[2],double y[101])
{
  double a;
  double b;
  double c;
  double tmp1;
  int k;
  b = params[0];
  c = params[1];
  tmp1=2*c*c;
  for (k = 0; k < 101; k++) {
    a = x[k] - b;
    y[k]=exp(-(a * a) /tmp1);
  }
}

/*三角函数输出在[-3,3]的101个点*/
static void fuzzy_trimf_a(const double x[101], const double params[3], double y[101])
{
  double a;
  double b;
  double c;
  double x_0;
  int i;
  a = params[0];
  b = params[1];
  c = params[2];
  for (i = 0; i < 101; i++) {
    x_0 = x[i];
    y[i]= 0.0;
    if ((a != b) && (a < x_0) && (x_0 < b)) {
      y[i] = 1.0 / (b - a) * (x_0 - a);
    }

    if ((b != c) && (b < x_0) && (x_0 < c)) {
      y[i] = 1.0 / (c - b) * (c - x_0);
    }
    if (x_0 == b) {
      y[i] = 1.0;
    }
  }
}

/* .计算输出Kp，Ki七条规则隶属曲线，在(-3,3)各取101个点*/
void fuzzy_Membershipcurve()
{
  double tmp_0[3];
  memset(&rtb_aggregatedKp_init[0], 0, 707 * sizeof(double));
  memset(&rtb_aggregatedKi_init[0], 0, 707 * sizeof(double));
  //Kp:NB
  tmp_0[0]=-3;
  tmp_0[1]=0.4247;
  fuz_evaluateCommonMembershipFcn(fuzzy_ConstP,tmp_0,&rtb_aggregatedKp_init[0*101]);
  //Kp:NM
  tmp_0[0] = -3.0;
  tmp_0[1] = -2.0;
  tmp_0[2] = -1.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKp_init[1*101]);
  //Kp:NS
  tmp_0[0] = -2.0;
  tmp_0[1] = -1.0;
  tmp_0[2] = 0.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKp_init[2*101]);
  //Kp:ZO
  tmp_0[0] = -1.0;
  tmp_0[1] = 0.0;
  tmp_0[2] = 1.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKp_init[3*101]);
  //Kp:PS
  tmp_0[0] = 0.0;
  tmp_0[1] = 1.0;
  tmp_0[2] = 2.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKp_init[4*101]);
  //Kp:PM
  tmp_0[0] = 1.0;
  tmp_0[1] = 2.0;
  tmp_0[2] = 3.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKp_init[5*101]);
  //Kp:PB
  tmp_0[0]=3;
  tmp_0[1]=0.4254;
  fuz_evaluateCommonMembershipFcn(fuzzy_ConstP,tmp_0,&rtb_aggregatedKp_init[6*101]);
  //Ki:NB
  tmp_0[0]=-3;
  tmp_0[1]=0.4247;
  fuz_evaluateCommonMembershipFcn(fuzzy_ConstP,tmp_0,&rtb_aggregatedKi_init[0*101]);
  //Ki:NM
  tmp_0[0] = -3.0;
  tmp_0[1] = -2.0;
  tmp_0[2] = -1.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKi_init[1*101]);
  //Ki:NS
  tmp_0[0] = -2.0;
  tmp_0[1] = -1.0;
  tmp_0[2] = 0.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKi_init[2*101]);
  //Ki:ZO
  tmp_0[0] = -1.0;
  tmp_0[1] = 0.0;
  tmp_0[2] = 1.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKi_init[3*101]);
  //Ki:PS
  tmp_0[0] = 0.0;
  tmp_0[1] = 1.0;
  tmp_0[2] = 2.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKi_init[4*101]);
  //Ki:PM
  tmp_0[0] = 1.0;
  tmp_0[1] = 2.0;
  tmp_0[2] = 3.0;
  fuzzy_trimf_a(fuzzy_ConstP, tmp_0, &rtb_aggregatedKi_init[5*101]);
  //Ki:PB
  tmp_0[0]=3;
  tmp_0[1]=0.4254;
  fuz_evaluateCommonMembershipFcn(fuzzy_ConstP,tmp_0,&rtb_aggregatedKi_init[6*101]);
}


/*fuzzy控制的初始化*/
void fuzzy_init()
{
  //1.制定模糊控制规则表：这里规则表与上面文章是一致的，只是E与EC交换横纵标位置！！！！！！
  //定义detalKP的模糊控制规则表，行为Ec(7个)，列为E（7个）
/*
             E
        -3    0     3
    -3  * * * * * * *
        * * * * * * *
        * * * * * * *
  Ec 0  * * * * * * *
        * * * * * * *
        * * * * * * *
     3  * * * * * * *
*/
  int ruleKp_init[49]=
  {
   PB,PB,PM,PM,PS,PS,ZO,         
   PB,PB,PM,PM,PS,ZO,ZO,          
   PM,PM,PM,PS,ZO,NS,NM,        
   PM,PS,PS,ZO,NS,NM,NM,        
   PS,PS,ZO,NS,NS,NM,NM,        
   ZO,ZO,NS,NM,NM,NM,NB,
   ZO,NS,NS,NM,NM,NB,NB,      
  };
  //定义detalKP的模糊控制规则表，行为Ec(7个)，列为E（7个）
  /*
             E
        -3    0     3
    -3  * * * * * * *
        * * * * * * *
        * * * * * * *
  Ec 0  * * * * * * *
        * * * * * * *
        * * * * * * *
     3  * * * * * * *
*/
  int ruleKi_init[49]=
  {
   NB,NB,NB,NM,NM,ZO,ZO,
   NB,NB,NM,NM,NS,ZO,ZO,
   NM,NM,NS,NS,ZO,PS,PS,
   NM,NS,NS,ZO,PS,PS,PM,
   NS,NS,ZO,PS,PS,PM,PM,
   ZO,ZO,PS,PM,PM,PB,PB,
   ZO,ZO,PS,PM,PB,PB,PB,
  };
  memcpy(&ruleKp[0],&ruleKp_init[0],sizeof(int)*49);
  memcpy(&ruleKi[0],&ruleKi_init[0],sizeof(int)*49);
  //2.计算输出Kp，Ki七条规则隶属曲线，在(-3,3)各取101个点
   fuzzy_Membershipcurve();
}

/* 模糊控制的一步函数*/
void fuzzy_step(ExtU_fuzzy_T *U,ExtY_fuzzy_T *Y)
{
  /* 输入输出 */
  ExtU_fuzzy_T fuzzy_U;
  ExtY_fuzzy_T fuzzy_Y;

  double tmp[2]={0};                        //E、EC输入
  double inputMFCache_E[7]={0};             //E的7个隶属度输出值
  double inputMFCache_EC[7]={0};            //EC的7个隶属度输出值
  double rtb_antecedentOutputs[49]={0};     //EC与E组合49个隶属度输出值
  double inputMFCache_Kp[7]={0};            //KP的7个隶属度输出值
  double inputMFCache_Ki[7]={0};            //Ki的7个隶属度输出值
  double rtb_aggregatedOutputs_Kp[707]={0}; //detal_Kp的(-3,3)七条隶属度曲线,各取101个点
  double rtb_aggregatedOutputs_Ki[707]={0}; //detal_Ki的(-3,3)七条隶属度曲线，各取101个点
  double Outputs_Kp[101]={0};               //detal_Kp的(-3,3)最终隶属度曲线, 取101个点
  double Outputs_Ki[101]={0};               //detal_Ki的(-3,3)最终隶属度曲线，取101个点
  double sumKp[2]={0};                         //Kp累加和
  double sumKi[2]={0};                         //Ki累加和
  double rtb_defuzzifiedOutputs[2]={0};     //模糊控制的detal_Kp,detal_ki的输出
  int i=0,j=0;
  double tmp_0[3]={0};
  int tmp_1[3]={0};
  double tmp_2[2]={0};

  //赋值
  fuzzy_U.E=U->E;
  fuzzy_U.Ec=U->Ec;

  /*1.输入限幅*/
  /*E输入的限值[-3，3]*/
  if (fuzzy_U.E > 3.0) {
    tmp[0] = 3.0;
  } else if (fuzzy_U.E < -3.0) {
    tmp[0] = -3.0;
  } else {
    tmp[0] = fuzzy_U.E;
  }
  /*Ec输入的限值[-3，3]*/
  if (fuzzy_U.Ec > 3.0) {
    tmp[1] = 3.0;
  } else if (fuzzy_U.Ec < -3.0) {
    tmp[1] = -3.0;
  } else {
    tmp[1] = fuzzy_U.Ec;
  }

  // printf("输入:%f %f\n",tmp[0],tmp[1]);    

  /*2.E,Ec七个隶属度计算*/
  fuzzy_createInputMFCache(tmp, inputMFCache_E,inputMFCache_EC);    //此函数的作用是量化输入的E和EC看交与哪个隶属函数，得出占比

  /*3.计算E,Ec的7*7的每一条规则的隶属度，并取其两者隶属度最小值*/
  /*rtb_antecedentOutputs[0*7+0]=E:NB|EC:NB  rtb_antecedentOutputs[0*7+1]:E:NB|EC:NM以此类推*/
  for (i = 0; i < 7; i++) {
      for (j = 0; j < 7; j++) {
      if(inputMFCache_E[j]<=inputMFCache_EC[i])      //EC的每一点和E的线来对比取最小的值
      {
        rtb_antecedentOutputs[i*7+j]=inputMFCache_E[j];
      }else{
        rtb_antecedentOutputs[i*7+j]=inputMFCache_EC[i];
      }
    }
  }

  for ( i = 0; i < 49; i++)           
  {
    
    switch (ruleKp[i])
    {
    case NB:{
       if (inputMFCache_Kp[0]<rtb_antecedentOutputs[i]){     //初始值都为0
        inputMFCache_Kp[0]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
        case NM:{
       if (inputMFCache_Kp[1]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[1]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case NS:{
       if (inputMFCache_Kp[2]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[2]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case ZO:{
       if (inputMFCache_Kp[3]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[3]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PS:{
       if (inputMFCache_Kp[4]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[4]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PM:{
       if (inputMFCache_Kp[5]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[5]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PB:{
       if (inputMFCache_Kp[6]<rtb_antecedentOutputs[i]){
        inputMFCache_Kp[6]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
    }
  }

    for ( i = 0; i < 49; i++)
  {
    switch (ruleKi[i])
    {
    case NB:{
       if (inputMFCache_Ki[0]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[0]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
        case NM:{
       if (inputMFCache_Ki[1]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[1]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case NS:{
       if (inputMFCache_Ki[2]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[2]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case ZO:{
       if (inputMFCache_Ki[3]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[3]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PS:{
       if (inputMFCache_Ki[4]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[4]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PM:{
       if (inputMFCache_Ki[5]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[5]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
          case PB:{
       if (inputMFCache_Ki[6]<rtb_antecedentOutputs[i]){
        inputMFCache_Ki[6]=rtb_antecedentOutputs[i]; 
       }
    }
      break;
    }
  }

  /* 4.计算输出Kp，Ki七条规则隶属曲线，在(-3,3)各取101个点*/
  memcpy(&rtb_aggregatedOutputs_Kp[0],&rtb_aggregatedKp_init[0],707 * sizeof(double));
  memcpy(&rtb_aggregatedOutputs_Ki[0],&rtb_aggregatedKi_init[0],707 * sizeof(double));
  for (j = 0; j < 7; j++)
  {
      tmp_1[0]=j*101;
      for (i = 0; i< 101; i++)
      {
        if(rtb_aggregatedOutputs_Kp[tmp_1[0]+i]>inputMFCache_Kp[j])
        {
          rtb_aggregatedOutputs_Kp[tmp_1[0]+i]=inputMFCache_Kp[j];
        }
      }
  }
  for (j = 0; j < 7; j++)         
  {
      tmp_1[1]=j*101;
      for (i = 0; i< 101; i++)
      {
        if(rtb_aggregatedOutputs_Ki[tmp_1[1]+i]>inputMFCache_Ki[j])
        {
          rtb_aggregatedOutputs_Ki[tmp_1[1]+i]=inputMFCache_Ki[j];
        }
      }
  }

  sumKp[0]=0;
  sumKi[0]=0;
  for ( i = 0; i < 101; i++)              //7组101个数中每次取各组的一个数据来比较取出最大值
  {
    tmp_2[0]=0;   //记录最大值
    tmp_2[1]=0;   //记录最大值
    for (j = 0; j < 7; j++)
    {
      tmp_1[2]=j*101+i;
      if (rtb_aggregatedOutputs_Kp[tmp_1[2]]>tmp_2[0])
      {
        tmp_2[0]=rtb_aggregatedOutputs_Kp[tmp_1[2]];
      }
      if (rtb_aggregatedOutputs_Ki[tmp_1[2]]>tmp_2[1])
      {
        tmp_2[1]=rtb_aggregatedOutputs_Ki[tmp_1[2]];
      }

    }    
    Outputs_Kp[i]=tmp_2[0];           
    sumKp[0]+=Outputs_Kp[i];  
    Outputs_Ki[i]=tmp_2[1];
    sumKi[0]+=Outputs_Ki[i];

  }

  /* 反模糊变换，计算出detal_Kp/detal_Ki的大小*/
  sumKp[1]=0;
  sumKi[1]=0;
  for ( i = 0; i < 101; i++)
  {
    sumKp[1]+=(fuzzy_ConstP[i]*Outputs_Kp[i]);    //相当于高度乘宽度   每个小面积叠加求和 积分
    sumKi[1]+=(fuzzy_ConstP[i]*Outputs_Ki[i]);
  }
  rtb_defuzzifiedOutputs[0]=sumKp[1]/sumKp[0];   //除以高度的累加和
  rtb_defuzzifiedOutputs[1]=sumKi[1]/sumKi[0];

  /* 输出detal_Kp/detal_Ki */
  fuzzy_Y.detal_Kp = rtb_defuzzifiedOutputs[0];
  fuzzy_Y.detal_Ki = rtb_defuzzifiedOutputs[1];

  Y->detal_Kp=fuzzy_Y.detal_Kp;
  Y->detal_Ki=fuzzy_Y.detal_Ki;

  // printf("输出:%f %f\n",Y->detal_Kp,Y->detal_Ki);    
}


// //2.PI：增量式PI控制部分
// //初始化
// void reset_pi(pi_info *pi,float Critical_KP,float Critical_KI)
// {
//  pi->kp = Critical_KP;
//  pi->ki = Critical_KI;
//  pi->Critical_KP=Critical_KP;
//  pi->Critical_KI=Critical_KI;
//  pi->error = 0;
//  pi->lastError = 0;
//  pi->dError = 0 ;
//  pi->output = 0 ;
//  pi->output_last = 0;
// }

// //增量式PID：u(k)=Kp * e(k-1)+Ki *e(t) +Kd *(e(k)-2e(k-1)+e(k-2))；
// float increment_pi(float error,pi_info *pi,float detal_kp,float detal_ki)//增量式PID
// {
//  //更新模糊PI系数
//  pi->kp = pi->Critical_KP+detal_kp;
//  pi->ki = pi->Critical_KI+detal_ki;
//  //增量PI控制
//  pi->error = error;
//  pi->dError = error - pi->lastError;
//  pi->lastError = error;
//  pi->output =(pi->kp*pi->dError)+(pi->ki*error) + pi->output_last;
//  pi->output_last = pi->output;
//  return pi->output;
// }


#include <sys/time.h>

double result1[3721]={0};
double result2[3721]={0};

//3.整体调用句柄0
void main(void)
{
  struct timeval start, end;
  int timeuse;

  ExtU_fuzzy_T u;
  ExtY_fuzzy_T y;

  gettimeofday(&start, NULL);
  fuzzy_init();
  gettimeofday(&end, NULL);
  timeuse = 1000000 * ( end.tv_sec - start.tv_sec ) + end.tv_usec - start.tv_usec;
  printf("timeofday=%fs\n", (double)timeuse/1000000);

  //1单点测试
  // gettimeofday(&start, NULL);
  // u.E=0;
  // u.Ec=3;
  // fuzzy_step(&u,&y);
  // gettimeofday(&end, NULL);
  // timeuse = 1000000 * ( end.tv_sec - start.tv_sec ) + end.tv_usec - start.tv_usec;
  // printf("timeofday=%fs\n", (double)timeuse/1000000);
  // printf("result:Kp:%f Ki:%f\n",y.detal_Kp,y.detal_Ki);

  //0.2精度//
  long int n1=0;
  long int n2=0;
  for (double i=-3; i<=3.1; i=i+0.2)
  {
    // n2++;
    // printf("%f\n" ,i);
    for(double j=-3; j<=3.1; j=j+0.2)
    {
        u.E=i;
        u.Ec=j;
        // fuzzy_init();
        fuzzy_step(&u,&y);
        result1[n1]=y.detal_Kp;
        result2[n1]=y.detal_Ki;
        n1++;
    }
  }

  printf("resultKp[i]:\n");
  for(int i=0;i<961;i++)
  {

  if (i==0)
  {
    printf("{");
  }

  if ((i==961-1))
  {
    printf("%f}",result1[i]);
  }else{
    if((i+1)%31==0 && i!=961-1)
    {
      printf("%f},\n{",result1[i]);
    }
    else{
      printf("%f,",result1[i]);
    }
  }
  }
  printf("\n");
  printf("\n");
  printf("\n");
  printf("resultKi[i]:\n");
  for(int i=0;i<961;i++)
  {
    if (i==0)
    {
      printf("{");
    }
    if ((i==961-1))
    {
      printf("%f}",result2[i]);
    }else{
      if((i+1)%31==0 && i!=961-1)
      {
        printf("%f},\n{"),result2[i];
      }
      else{
        printf("%f,",result2[i]);
      }
    }
  }
}

与mat结果验证：
matlab输入E，EC的[-3:3]区间，每隔0.2取一个点，共计[31 31]个矩阵，输出结果：

%激励数据
function [e,ec] = fcn(u)
n=0.2
tempE=0;
tempEC=0;
chushu=fix(u/(6/n+1));
yshu=rem(u,6/n+1);
tempE=-3+chushu*0.2;
tempEC=-3+yshu*0.2;
e=tempE;
ec=tempEC;

clc
%输出结果表格
result =data.Data;
x=0.2;
y1=(6/0.2+1);
y2=(6/0.2+1)^2;
fprintf("Kp:\n");
for n=0:1:y2-1
    if(n==0)
        fprintf("{");
    end
     if(n==y2-1)
        fprintf("%f}",result(n+1,3));
     else
         if(rem((n+1),y1)==0 && n~=y2-1)
              fprintf("%f},\n{",result(n+1,3));
         else
             fprintf("%f,",result(n+1,3));
         end
     end
end
fprintf("\n\nKi:\n");
for n=0:1:y2-1
    if(n==0)
        fprintf("{");
    end
     if(n==y2-1)
        fprintf("%f}",result(n+1,4));
     else
         if(rem((n+1),y1)==0 && n~=y2-1)
              fprintf("%f},\n{",result(n+1,4));
         else
             fprintf("%f,",result(n+1,4));
         end
     end
end

自己写的程序输出结果：

验证通过！！！！！到此结束！

4.4 实际工程应用

在实际工程应用中，没必要去让程序去跑模糊控制代码，运算量大，计算出时间太长了，不利于控制，直接选择在matlab模型运行或者电脑源代码运行，得到所需的计算结果，直接去查表得出结果就ok，方便快捷！

5. 全部资源

资源：链接：https://download.youkuaiyun.com/download/pengrunxin/89423301 : link，[matlab版本2018A],低于这个版本自己解决

做了好久啊，里面还有一部分没完善的，太累了。制作不易，关注加点赞一波，啊啊啊啊，谢谢！