41 求数组中缺失的第一个正数

点击此处返回总目录   【题目】 【分析】 假设数组的长度为4，数组最多放四个正数。那数组中没出现的最小正整数只能是1,2,3,4或者5。   要求时间复杂度为o(n)，意思是可以通过1趟遍历，2趟遍历，3趟遍历...得到。 我们一般能想到的方法： 1. 首先排序，然后一趟查找。时间复杂度为nlogn，不行。 2. 从1开始查找，不行，时间复杂度为n2。 3. 异或操作，不行。 4. 另起一个数组或者Set，不行，空间复杂度为o(n)。       【方法一】 利用645题方法三。 通过负号来记录该位置有没有出现过正确的数。但是因为数组中有负数，所以要先处理一下。 我们的想法是遍历一遍数组，如果出现了1，则把第0位变成负数。如果出现了n，则把第n-1位变成负数。 所以，首先要把数组中的负数都处理掉，否则看到负数我们无法判断是本来是负数还是我们改成的负数。 处理成多少合适呢？如果处理成0，那么加上负号之后还是0，就没法判断了。所以，我们处理成了len+1。   把0也变成len+1也是同样的原因。   至于把大于len的数也变成了len+1，就是顺手做了，也可以不处理。 这样就变成了类似以下的数组： [2,9,2,4,9,1,9,3] 剩下的就跟以前一样，如果遇到的数在[1,n]之间，就把相应位变成负的，做为标记。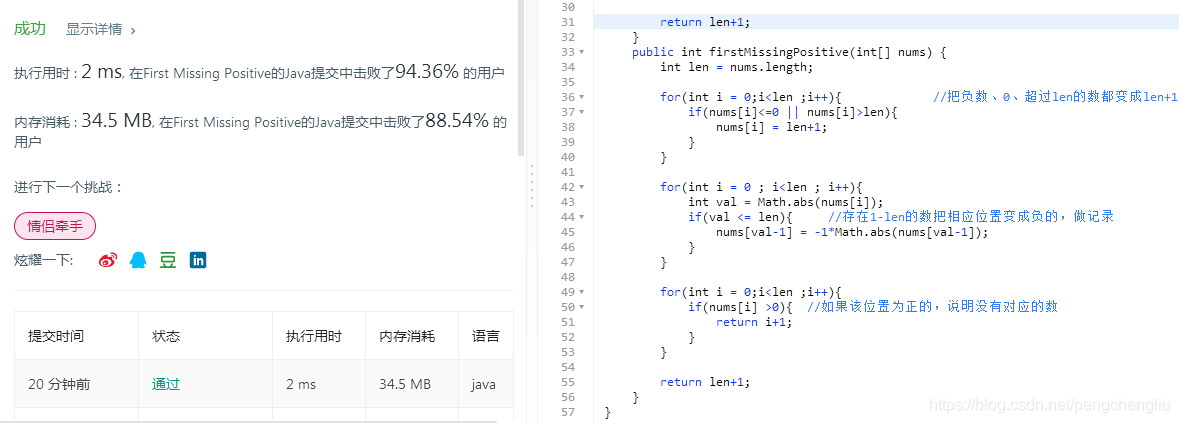     代码：   结果：       【方法二】 利用题目  一个数组的元素为1~n，在o(n)的时间内对数组排序 的思想和延伸，将1-n的元素归位。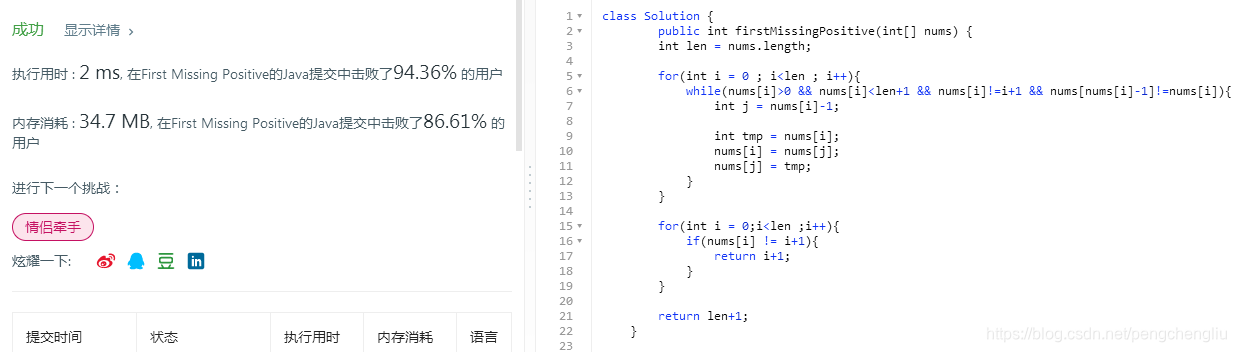   代码：   结果：