POJ2810 完美立方：给定整数N，找出所有小于N的a、b、c、d，使得b、c、d的立方和等于a的立方

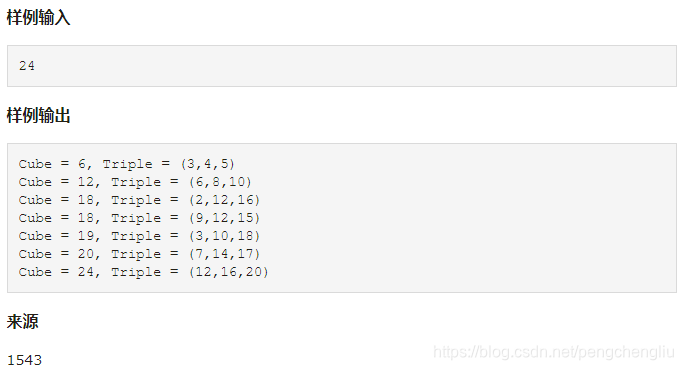
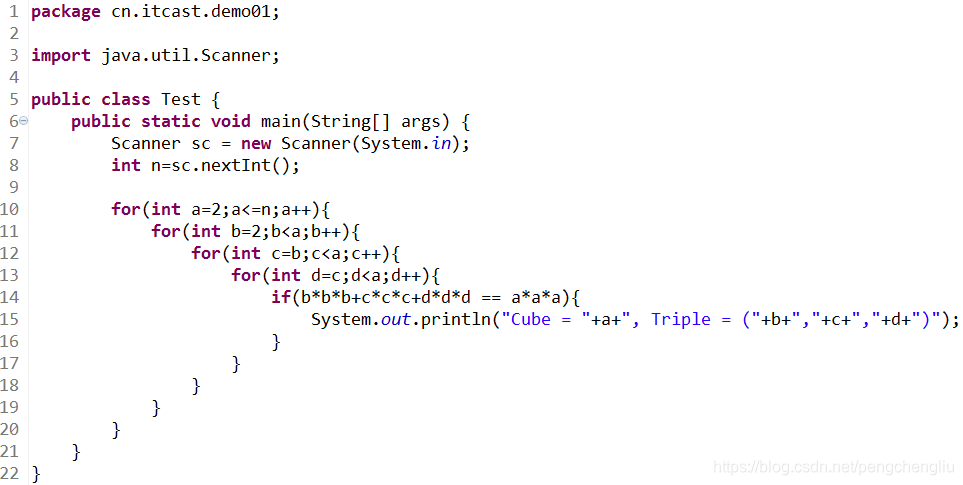
点击此处返回总目录         什么是枚举？ 枚举是基于逐个尝试答案的一种问题求解策略。一个一个答案试。 我们知道解决问题，有时候就用笨办法。一个一个试。   要注意的是：虽然是枚举，但有时可以通过缩小枚举的范围以及合理设计枚举的顺序，达到提高枚举效率的目的。       【题目】           【分析】 这个题怎么做呢？看上去像是个数学问题，但是找不到什么规律。只能一个一个试。怎么试呢？  用四层循环。但是枚举的时候要注意，没必要试的就跳过，不需要a,b,c,d从2到N都试一下，有的根本就不需要试。我们可以通过设计枚举的方式，避免尝试根本不是答案的方案。把a放到最外层，d在最里层就可以做到这一点。   1. 输出的时候a从小往大输出的，所以便利的时候a从小的开始。 2. 对于范围,我们通过设计变量的范围，可以避免根本就不是答案的情况。     a的枚举范围：[2, N]        b的范围：[2, a-1]                 c的范围：[b, a-1]     d的范围：[c, a-1]       如果通过更精准的一点思考，把abcd的范围缩小一点也行，但是一般来说，除非你的效率特别关键，你也不用想那么多，大致的一个粗略的范围，够用就行。当然如果不用动脑子，就能够把范围缩小一点，那就缩小。       【代码】   【结果】         【总结】 通过这道题，我们可以看到，即使是枚举，也不是把所有方案都去试。有的方案是不用去试的，我们可以通过缩小枚举的范围以及合理设计枚举的顺序，达到提高枚举效率的目的。