1、向量的内积(点乘),外积(叉乘)
向量的内积(点乘),外积(叉乘)的代数定义与几何定义;
https://zhuanlan.zhihu.com/p/359975221
2、向量的投影与正交投影
参考资料:
https://blog.youkuaiyun.com/wxc971231/article/details/122789265
2.1、投影问题数学表达
二维平面投影,如下将b向量投影到向量a方向,得到b向量在a向量的分量p;数学表达为:已知向量a和b如下定义:
a={xayaza}b={xbybzb}
a=\left\{\begin{array}{l}
x_a \\
y_a \\
z_a
\end{array}\right\} b=\left\{\begin{array}{l}
x_b \\
y_b \\
z_b
\end{array}\right\}
a=⎩⎨⎧xayaza⎭⎬⎫b=⎩⎨⎧xbybzb⎭⎬⎫
具体情况如下图:
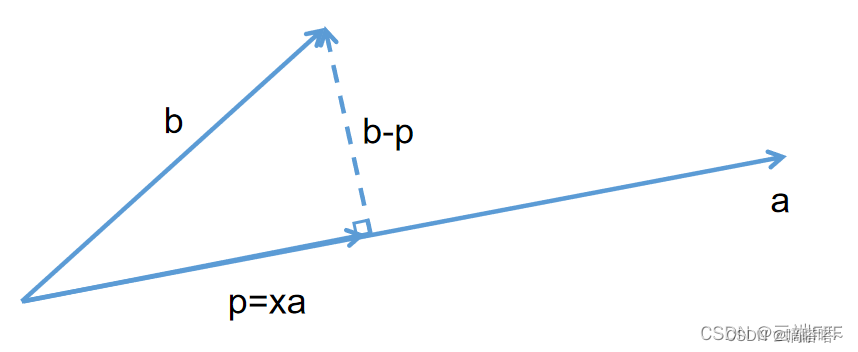
求向量p 关于向量a和b的表达式?
2.2、求解投影矩阵
如图可见向量 b−p 与向量a 正交,內积为 0,即有
a⊤(b−p)=a⊤(b−xa)=0⇒x=a⊤ba⊤a/∗注意x式一个系数,行乘列为向量内积∗/⇒p=ax=aa⊤ba⊤a=(aa⊤a⊤a)b \begin{aligned}
& \mathbf{a}^{\top}(\mathbf{b}-\mathbf{p})=\mathbf{a}^{\top}(\mathbf{b}-\mathrm{x} \mathbf{a})=\mathbf{0} \\
\Rightarrow & \mathbf{x}=\frac{\mathbf{a}^{\top} \mathbf{b}}{\mathbf{a}^{\top} \mathbf{a}} &/* 注意x式一个系数,行乘列为向量内积 */\\
\Rightarrow & \mathbb{p}=\mathbf{ax}=\mathbf{a} \frac{\mathbf{a}^{\top} \mathbf{b}}{\mathbf{a}^{\top} \mathbf{a}}=\left(\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right) \mathbf{b}
\end{aligned} ⇒⇒a⊤(b−p)=a⊤(b−xa)=0x=a⊤aa⊤bp=ax=aa⊤aa⊤b=(a⊤aaa⊤)b/∗注意x式一个系数,行乘列为向量内积∗/
其中
(aa⊤a⊤a)
\begin{aligned}
\left(\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right)
\end{aligned}
(a⊤aaa⊤)
P=aa⊤a⊤a\mathbf{P}=\frac{\mathrm{aa}^{\top}}{\mathbf{a}^{\top} \mathrm{a}}P=a⊤aaa⊤ 称为投影矩阵,记作PPP。
2.3、投影矩阵PPP的性质
- 分母a⊤a\mathbf{a}^{\top} \mathbf{a}a⊤a 是向量内积,是个常数,不管它
- 分子 aa⊤\mathbf{a} \mathbf{a}^{\top}aa⊤ ,这是个矩阵,显然有 rank(A)=1\operatorname{rank}(\mathbf{A})=1rank(A)=1 ,其列空间就是 ka} ,因此用投影矩阵左乘向量会把向量变换到其列空间 kak \mathbf{a } \text { ,因此用投影矩阵左乘向量会把向量变换到其列空间 } k \mathbf { a }}ka} ,因此用投影矩阵左乘向量会把向量变换到其列空间 ka中,实现投影
- aa⊤\mathbf{a} \mathbf{a}^{\top}aa⊤ 对称,所以 P\boldsymbol{P}P 是对称矩阵, P=P⊤\mathbf{P}=\mathbf{P}^{\top}P=P⊤
- 重复投影两次,结果不变,即有 P2=P\mathbf{P}^2=\mathbf{P}P2=P
- 另外提一句,假设向量 䙵两夹角为 θ\thetaθ ,常见的向量内积
a⊤b=∥b∥⋅∥a∥⋅cos(θ) \mathbf{a}^{\top} \mathbf{b}=\|\mathbf{b}\| \cdot\|\mathbf{a}\| \cdot \cos (\theta) a⊤b=∥b∥⋅∥a∥⋅cos(θ)
计算的就是一个向量的模乘以另一个向量在此向量上投影的模长。如果把其中某一个向量的模长设为 1 (即变为单位向量),最后再乘以该向量,就得到投影向量,即
a\mathbf{a}a 投影到单位向量 b\mathbf{b}b 为: (a⊤b)b=(b⊤a)b=∥a∥cos(θ)b\left(\mathbf{a}^{\top} \mathbf{b}\right) \mathbf{b}=\left(\mathbf{b}^{\top} \mathbf{a}\right) \mathbf{b}=\|\mathbf{a}\| \cos (\theta) \mathbf{b}(a⊤b)b=(b⊤a)b=∥a∥cos(θ)b, 其中 ∥b∥=1\|\mathbf{b}\|=1∥b∥=1
b\mathbf{b}b 投影到单位向量 a\mathbf{a}a 为: (a⊤b)a=(b⊤a)a=∥b∥cos(θ)a\left(\mathbf{a}^{\top} \mathbf{b}\right) \mathbf{a}=\left(\mathbf{b}^{\top} \mathbf{a}\right) \mathbf{a}=\|\mathbf{b}\| \cos (\theta) \mathbf{a}(a⊤b)a=(b⊤a)a=∥b∥cos(θ)a, 其中 ∥a∥=1\|\mathbf{a}\|=1∥a∥=1
当投影方向不是单位向量时,增加其模的倒数进行缩放,如上图中的 P=∥b∥cos(θ)a∥a∥\mathbf{P}=\|\mathbf{b}\| \cos (\theta) \frac{\mathbf{a}}{\|\mathbf{a}\|}P=∥b∥cos(θ)∥a∥a
2.4、正交投影矩阵
已知向量b在向量a上的投影向量 ppp可以如下表示:
p=(aa⊤a⊤a)b \begin{aligned}
& \mathbb{p}=\left(\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right) \mathbf{b}
\end{aligned} p=(a⊤aaa⊤)b
则向量b在向量a正交方向投影为 b-p;表达式如下:
b−p=Ib−(aa⊤a⊤a)b=(I−aa⊤a⊤a)b \begin{aligned}
& b-p=\mathbf{Ib}-\left(\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right) \mathbf{b} = \left(\mathbf{I}-\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right) \mathbf{b}
\end{aligned} b−p=Ib−(a⊤aaa⊤)b=(I−a⊤aaa⊤)b
因正交投影矩阵表达式为:(I−aa⊤a⊤a)\left(\mathbf{I}-\frac{\mathbf{a} \mathbf{a}^{\top}}{\mathbf{a}^{\top} \mathbf{a}}\right) (I−a⊤aaa⊤)
3、Householder 变换与QR分解
推荐视频资料:
https://m.bilibili.com/video/BV1FB4y1j7pA?buvid=XY1BC9D1023376660B90270930FC3357FA99A&from_spmid=united.player-video-detail.drama-float.0&is_story_h5=false&mid=EMknszTdXIk3B70T%2BkLvLQ%3D%3D&p=1&plat_id=114&share_from=ugc&share_medium=android&share_plat=android&share_session_id=c92f3465-b268-4b3e-b014-5c5cfa3621d4&share_source=WEIXIN&share_tag=s_i&spmid=united.player-video-detail.0.0×tamp=1700552919&unique_k=YcPByru&up_id=1235616254&code=0417lc100dVc4R1xoS300o6xgY07lc1P&state=
推荐书本:矩阵分析与应用张贤达第一版,第4章内容。
3.1、Householder 变换与 Householder 矩阵
3.1.1、Householder 变换
考虑如下场景:已知向量xxx和向量www,求解向量yyy,向量yyy具有以下特点:
根据向量www可以确认其垂直平面,如下图灰色面部分;向量yyy为向量xxx相对于灰色面部分的镜像向量yyy;由于向量xxx和向量yyy满足镜像关系,所以向量xxx与向量yyy长度相同。
因此Householder 变换也称为镜像变换。
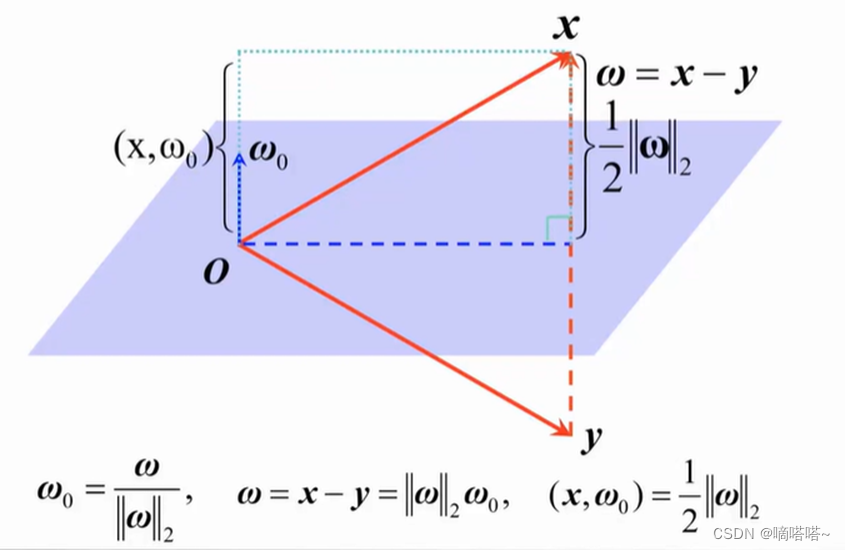
ω0=ω∥ω∥2,ω=x−y=∥ω∥2ω0,∥ω∥2=2(x,ω0)=2ω0Txx−y=2(ω0Tx)ω0=2ω0(ω0Tx)=2ω(ωTx)∥ω∥22=2(ωωT)xωTωy=x−2ωωTωTωx=(I−2ωTωωωT)x=H(ω)x \begin{gathered} \omega_0=\frac{\omega}{\|\omega\|_2}, \quad \omega=x-y=\|\omega\|_2 \omega_0, \quad\|\omega\|_2=2\left(x, \omega_0\right)=2 \omega_0^T x \\ x-y=2\left(\omega_0^T x\right) \omega_0=2 \omega_0\left(\omega_0^T x\right)=2 \frac{\omega\left(\omega^T x\right)}{\|\omega\|_2^2}=2 \frac{\left(\omega \omega^T\right) x}{\omega^T \omega} \\ y=x-2 \frac{\omega \omega^T}{\omega^T \omega} x=\left(I-\frac{2}{\omega^T \omega} \omega \omega^T\right) x=H(\omega) x \end{gathered} ω0=∥ω∥2ω,ω=x−y=∥ω∥2ω0,∥ω∥2=2(x,ω0)=2ω0Txx−y=2(ω0Tx)ω0=2ω0(ω0Tx)=2∥ω∥22ω(ωTx)=2ωTω(ωωT)xy=x−2ωTωωωTx=(I−ωTω2ωωT)x=H(ω)x
设 ω∈Rn,ω≠0\omega \in \mathbf{R}^n, \omega \neq 0ω∈Rn,ω=0, 称初等矩阵为Householder矩阵:
H(ω)=I−2ωTωωωT
\boldsymbol{H}(\boldsymbol{\omega})=\boldsymbol{I}-\frac{2}{\boldsymbol{\omega}^T \omega} \boldsymbol{\omega} \boldsymbol{\omega}^T
H(ω)=I−ωTω2ωωT
注意:向量www为列向量,所以
分子:ωωT\boldsymbol{\omega} \boldsymbol{\omega}^TωωT 是一个3*3的对称矩阵
分母:ωTω\boldsymbol{\omega}^T \omegaωTω是一个数值,向量的内积等于向量模长的平方。
3.1.2、Householder矩阵的性质
-
对称性: H(ω)T=H(ω)\boldsymbol{H}(\boldsymbol{\omega})^T=\boldsymbol{H}(\boldsymbol{\omega})H(ω)T=H(ω)
H(ω)T=(I−2ωTωωω)T=I−2ωTω(ωω)T=I−2ωTωωωT=H(ω) \boldsymbol{H}(\boldsymbol{\omega})^T=\left(\boldsymbol{I}-\frac{2}{\boldsymbol{\omega}^T \boldsymbol{\omega}} \boldsymbol{\omega} \boldsymbol{\omega}\right)^T=\boldsymbol{I}-\frac{2}{\boldsymbol{\omega}^T \boldsymbol{\omega}}(\boldsymbol{\omega} \boldsymbol{\omega})^T\\ =\boldsymbol{I}-\frac{2}{\boldsymbol{\omega}^T \boldsymbol{\omega}} \boldsymbol{\omega} \boldsymbol{\omega}^T=\boldsymbol{H}(\boldsymbol{\omega}) H(ω)T=(I−ωTω2ωω)T=I−ωTω2(ωω)T=I−ωTω2ωωT=H(ω) -
正交性: H(ω)TH(ω)=I\boldsymbol{H}(\boldsymbol{\omega})^T \boldsymbol{H}(\boldsymbol{\omega})=\boldsymbol{I}H(ω)TH(ω)=I
H(ω)TH(ω)=(I−2ωTωωω2=I−2ωTωωωT−2ωTωωωT+(2ωTω)2(ωωJ)(ωωT)=I−4ωTωωωT+4(ωTω)2ω(ωTω)ωT=I \begin{aligned} H(\omega)^T H(\omega)=\left(I-\frac{2}{\omega^T \omega} \omega \omega^2=I-\frac{2}{\omega^T \omega} \omega \omega^T-\frac{2}{\omega^T \omega} \omega \omega^T\right. & +\left(\frac{2}{\omega^T \omega}\right)^2\left(\omega \omega^J\right)\left(\omega \omega^T\right) \\ =\boldsymbol{I}-\frac{4}{\omega^T \omega} \omega \omega^T+\frac{4}{\left(\omega^T \omega\right)^2} \omega\left(\omega^T \omega\right) \omega^T=\boldsymbol{I} \end{aligned} H(ω)TH(ω)=(I−ωTω2ωω2=I−ωTω2ωωT−ωTω2ωωT=I−ωTω4ωωT+(ωTω)24ω(ωTω)ωT=I+(ωTω2)2(ωωJ)(ωωT) -
如果 H(ω)x=y\boldsymbol{H}(\boldsymbol{\omega}) \boldsymbol{x}=\boldsymbol{y}H(ω)x=y, 则 ∥y∥2=∥x∥2\|\boldsymbol{y}\|_2=\|\boldsymbol{x}\|_2∥y∥2=∥x∥2 (长度不变)
∥y∥22=yTy=(H(ω)x)T(H(ω)x)=xT(H(ω)TH(ω))x=xTx=∥x∥22 \|\boldsymbol{y}\|_2^2=\boldsymbol{y}^T \boldsymbol{y}=(\boldsymbol{H}(\boldsymbol{\omega}) \boldsymbol{x})^T(\boldsymbol{H}(\boldsymbol{\omega}) \boldsymbol{x}) \\ = \boldsymbol{x}^T\left(\boldsymbol{H}(\boldsymbol{\omega})^T \boldsymbol{H}(\boldsymbol{\omega})\right) \boldsymbol{x}=\boldsymbol{x}^T \boldsymbol{x}=\|\boldsymbol{x}\|_2^2 ∥y∥22=yTy=(H(ω)x)T(H(ω)x)=xT(H(ω)TH(ω))x=xTx=∥x∥22 -
H(ω)\boldsymbol{H}(\boldsymbol{\omega})H(ω) 的特征值为 n−1n-1n−1 个 1 和一个 -1 。
所以行列式的值为 ∣H(ω)∣=−1|\boldsymbol{H}(\boldsymbol{\omega})|=-1∣H(ω)∣=−1 -
由于H(ω)H(\omega )H(ω)是一个对称的正交矩阵,因此有以下等式成立。
H(ω)=H(ω)T=H(ω)−1H(\omega ) = H{(\omega )^T} = H{(\omega )^{ - 1}}H(ω)=H(ω)T=H(ω)−1
3.1.3、Householder 变换的意义
设 x,y∈Rn,x≠y,∥x∥2=∥y∥2x, y \in \mathbf{R}^n, x \neq y,\|x\|_2=\|y\|_2x,y∈Rn,x=y,∥x∥2=∥y∥2, 取 ω=x−y\omega=x-yω=x−y 则
H(ω)x=y
\boldsymbol{H}(\omega) x=y
H(ω)x=y
这个等式的意义其实包含了xywxywxyw三个向量之间的关系,当满足向量xxx的模长等于向量yyy的模长,且向量www满足w=x−yw=x-yw=x−y这两个条件,则上面等式恒成立。
此等式有以下特殊应用,设 x=(x1,x2,⋯ ,xn)T∈Rn\boldsymbol{x}=\left(x_1, x_2, \cdots, x_n\right)^T \in \mathbf{R}^nx=(x1,x2,⋯,xn)T∈Rn 且 x≠0\boldsymbol{x} \neq \boldsymbol{0}x=0, 我们希望将n维变量xxx转换为向量y=±∥x∥2e1y = \pm\|x\|_2 e_1y=±∥x∥2e1 的形式,其中 e1=(1,0,...,0)T{{\rm{e}}_1} = {(1,0,...,0)^T}e1=(1,0,...,0)T;此时满足了向量x,yx,yx,y模长相等的条件,取 ω=x±∥x∥2e1\omega=\boldsymbol{x} \pm\|x\|_2 e_1ω=x±∥x∥2e1 则满足了w=x−yw=x-yw=x−y的条件;因此下面恒等关系成立。
H(ω)x=∓∥x∥2e1.
H(\omega) x=\mp\|x\|_2 e_1 .
H(ω)x=∓∥x∥2e1.
由于H(ω)H(\omega )H(ω)是一个对称的正交矩阵,因此有以下等式成立:H(ω)=H(ω)T=H(ω)−1H(\omega ) = H{(\omega )^T} = H{(\omega )^{ - 1}}H(ω)=H(ω)T=H(ω)−1;根据上面两式子得到以下结论:H(ω)x=∓∥x∥2e1H(ω)−1H(ω)x=H(ω)−1∥x∥2e1⇒x=H(ω)−1∥x∥2e1⇒x=H(ω)∥x∥2e1\begin{array}{ccc}
{H(\omega )x = \mp {{\left\| x \right\|}_2}{e_1}}\\
{H{{(\omega )}^{ - 1}}H(\omega )x = H{{(\omega )}^{ - 1}}{{\left\| x \right\|}_2}{e_1}}\\
{ \Rightarrow x = H{{(\omega )}^{ - 1}}{{\left\| x \right\|}_2}{e_1}}\\
{ \Rightarrow x = H(\omega ){{\left\| x \right\|}_2}{e_1}}
\end{array}H(ω)x=∓∥x∥2e1H(ω)−1H(ω)x=H(ω)−1∥x∥2e1⇒x=H(ω)−1∥x∥2e1⇒x=H(ω)∥x∥2e1
使用Householder 变换可以将一个普通向量xxx分解为一个对阵正交矩阵H(ω)H(\omega )H(ω)乘以一个单位向量∓∥x∥2e1\mp {\left\| x \right\|_2}{e_1}∓∥x∥2e1的形式。
3.1.4、应用举例
例: 求Householder矩阵 H\mathrm{H}H, 使得 Hx=y\mathrm{Hx}=\mathrm{y}Hx=y
已知x=(−3,0,4)Tx=(-3,0,4)^Tx=(−3,0,4)T,那向量yyy只需要满足模长与向量xxx相同即可,所以向量yyy的取值很多,可以为y=(5,0,0)Ty=(5,0,0)^Ty=(5,0,0)T或y=(0,5,0)Ty=(0,5,0)^Ty=(0,5,0)T或y=(1,1,23)Ty=(1,1,\sqrt {23} )^Ty=(1,1,23)T,这里我们取:y=(0,0,5)Ty=(0,0,5)^Ty=(0,0,5)T进行计算。
x=(−3,0,4)T,y=(0,0,5)Tω=x−y=(−3,0,−1)TωTω=10H(ω)=I−2ωωTωTω=(111)−210(−301)(−3,0,−1)=(−450−35010−35045) \begin{aligned} & x=(-3,0,4)^T, y=(0,0,5)^T \\ & \omega=x-y=(-3,0,-1)^T \quad \omega^T \omega=10 \\ & H(\omega)=I-2 \frac{\omega \omega^T}{\omega^T \omega}=\left(\begin{array}{ccc} 1 & & \\ & 1 & \\ & & 1 \end{array}\right)-\frac{2}{10}\left(\begin{array}{c} -3 \\ 0 \\ 1 \end{array}\right)(-3,0,-1)=\left(\begin{array}{ccc} -\frac{4}{5} & 0 & -\frac{3}{5} \\ 0 & 1 & 0 \\ -\frac{3}{5} & 0 & \frac{4}{5} \end{array}\right) \end{aligned} x=(−3,0,4)T,y=(0,0,5)Tω=x−y=(−3,0,−1)TωTω=10H(ω)=I−2ωTωωωT=111−102−301(−3,0,−1)=−540−53010−53054
3.2、QR分解
3.2.1 矩阵分解的目的
矩阵分解的目的就是简化线程方程组求解,降低计算难度和计算量。
如果 A∈Rm×n(m≥n),r(A)=n\boldsymbol{A} \in \mathrm{R}^{m \times n}(m \geq n), r(\boldsymbol{A})=nA∈Rm×n(m≥n),r(A)=n,
A=Q(RIO)=QR
A=Q\left(\begin{array}{c}
R_I \\
O
\end{array}\right)=Q R
A=Q(RIO)=QR
其中 QQQ 为正交阵, R1R_1R1 为对角元非零的上三角矩阵;这样矩阵可以变成如下形式:
A=QR
A=Q R
A=QR
QQQ 为对称正交阵, RRR 为上三角阵,因此线程方程组可以改写成以下形式:
Ax=b⟶A=QR{Qy=bRx=y⟺Rx=QTb=Qb
\boldsymbol{A x}=\boldsymbol{b} \stackrel{A=Q R}{\longrightarrow}\left\{\begin{array}{l}
Q y=b \\
R x=y
\end{array} \Longleftrightarrow Rx=Q^T b=Q b\right.
Ax=b⟶A=QR{Qy=bRx=y⟺Rx=QTb=Qb
这样xxx的系数阵 R1R_1R1 为对角元非零的上三角矩阵;通过将数据回代进入方程就可以求解xxx
3.2.2、QR分解举例
使用Householder变换将矩阵A分解为对称矩阵乘以对角非零的上三角矩阵,其中
A=(11123121−5)A=\left(\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & 1 \\
2 & 1 & -5
\end{array}\right)A=12213111−5
-
第一取出第一列a1a_1a1进行Householder变换
a1=(122),∥a1∥2=3a_1=\left(\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right), \quad\left\|a_1\right\|_2=3a1=122,∥a1∥2=3,
w1w_1w1取值为:
ω1=a1−∥a1∥2e1=(122)−(300)=(−222)\omega_1=a_1-\left\|a_1\right\|_2 e_1=\left(\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right)-\left(\begin{array}{l} 3 \\ 0 \\ 0 \end{array}\right)=\left(\begin{array}{c} -2 \\ 2 \\ 2 \end{array}\right)ω1=a1−∥a1∥2e1=122−300=−222
Q1=H(ω1)=I−2ω1Tω1ω1ω1T=(1323232313−2323−2313), Q_1=H\left(\omega_1\right)=\boldsymbol{I}-\frac{2}{\omega_1^{\mathrm{T}} \omega_1} \omega_1 \omega_1^{\mathrm{T}}=\left(\begin{array}{ccc} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{1}{3} & \frac{-2}{3} \\ \frac{2}{3} & \frac{-2}{3} & \frac{1}{3} \end{array}\right) \text {, }Q1=H(ω1)=I−ω1Tω12ω1ω1T=31323232313−2323−231,
Q1A=(33−73011330−1−53)=(3bT0A2){Q_1}{\bf{A}} = \left( {\begin{array}{ccc} 3&3&{ - \frac{7}{3}}\\ 0&1&{\frac{{13}}{3}}\\ 0&{ - 1}&{ - \frac{5}{3}} \end{array}} \right) = \left( {\begin{array}{ccc} 3&{{{\bf{b}}^{\rm{T}}}}\\ {\bf{0}}&{{{\bf{A}}_2}} \end{array}} \right)Q1A=30031−1−37313−35=(30bTA2) -
根据上面等式,A2=(1133−1−53){A_2} = \left( {\begin{array}{ccc} 1&{\frac{{13}}{3}}\\ { - 1}&{ - \frac{5}{3}} \end{array}} \right)A2=(1−1313−35),继续对A2A_2A2进行Householder变换;
a~1=(1−1),∥a~1∥2=2,\widetilde{\boldsymbol{a}}_1=\left(\begin{array}{c} 1 \\ -1 \end{array}\right),\left\|\widetilde{\boldsymbol{a}}_1\right\|_2=\sqrt{2},a1=(1−1),∥a1∥2=2,
ω~2=a~1−∥a~1∥2e1=(1−1)−(20)=(1−2−1)\widetilde{\boldsymbol{\omega}}_2=\widetilde{\boldsymbol{a}}_1-\left\|\widetilde{\boldsymbol{a}}_1\right\|_2 \boldsymbol{e}_1=\left(\begin{array}{c} 1 \\ -1 \end{array}\right)-\left(\begin{array}{c} \sqrt{2} \\ 0 \end{array}\right)=\left(\begin{array}{c} 1-\sqrt{2} \\ -1 \end{array}\right)ω2=a1−∥a1∥2e1=(1−1)−(20)=(1−2−1)
Q~2=H(ω~2)=I−2ω~2Tω~2ω~2ω~2T=12(2−2−2−2)\widetilde{\boldsymbol{Q}}_2=\boldsymbol{H}\left(\widetilde{\boldsymbol{\omega}}_2\right)=\boldsymbol{I}-\frac{2}{\widetilde{\boldsymbol{\omega}}_2^{\mathrm{T}} \widetilde{\boldsymbol{\omega}}_2} \widetilde{\boldsymbol{\omega}}_2 \widetilde{\boldsymbol{\omega}}_2^{\mathrm{T}}=\frac{1}{2}\left(\begin{array}{cc} \sqrt{2} & -\sqrt{2} \\ -\sqrt{2} & -\sqrt{2} \end{array}\right)Q2=H(ω2)=I−ω2Tω22ω2ω2T=21(2−2−2−2)
Q~2A2=(H(ω~2)a~1,H(ω~2)a~2)=(2320−432)\widetilde{\boldsymbol{Q}}_2 \boldsymbol{A}_2=\left(\boldsymbol{H}\left(\widetilde{\boldsymbol{\omega}}_2\right) \widetilde{\boldsymbol{a}}_1, \boldsymbol{H}\left(\widetilde{\boldsymbol{\omega}}_2\right) \widetilde{\boldsymbol{a}}_2\right)=\left(\begin{array}{cc} \sqrt{2} & 3 \sqrt{2} \\ 0 & -\frac{4}{3} \sqrt{2} \end{array}\right)Q2A2=(H(ω2)a1,H(ω2)a2)=(2032−342) -
构造Q2=(10T0Q~2)=(10002−20−2−2){Q_2} = \left( {\begin{array}{ccc} 1&{{0^{\rm{T}}}}\\ 0&{\mathop {{ \widetilde{Q}_2}}\limits } \end{array}} \right) = \left( {\begin{array}{ccc} 1&0&0\\ 0&{\sqrt 2 }&{ - \sqrt 2 }\\ 0&{ - \sqrt 2 }&{ - \sqrt 2 } \end{array}} \right)Q2=(100TQ2)=10002−20−2−2
由于Q~2{ \widetilde{Q}_2}Q2是Householder矩阵,具有对称正交的性质;所以构造的Q2{Q_2}Q2同样是对称正交矩阵,也是House矩阵。 -
将Q2Q1A=Q2(3bT0A2)=(3bT0Q~2A2)=(33−73023200−432)=R\boldsymbol{Q}_2 \boldsymbol{Q}_1 \boldsymbol{A}=Q_2\left(\begin{array}{cc} 3 & \boldsymbol{b}^{\mathrm{T}} \\ 0 & \boldsymbol{A}_2 \end{array}\right)=\left(\begin{array}{cc} 3 & \boldsymbol{b}^{\mathrm{T}} \\ 0 & \widetilde{\boldsymbol{Q}}_2 \boldsymbol{A}_2 \end{array}\right)=\left(\begin{array}{ccc} 3 & 3 & -\frac{7}{3} \\ 0 & \sqrt{2} & 3 \sqrt{2} \\ 0 & 0 & -\frac{4}{3} \sqrt{2} \end{array}\right)=\boldsymbol{R}Q2Q1A=Q2(30bTA2)=(30bTQ2A2)=300320−3732−342=R
Q2Q1A=RA=(Q2Q1)−1RA=(Q2Q1)TRA=(Q1TQ2T)RA=(Q1Q2)R⇒A=QR\begin{array}{l} {Q_2}{Q_1}A = R\\ A = {\left( {{Q_2}{Q_1}} \right)^{ - 1}}R\\ A = {\left( {{Q_2}{Q_1}} \right)^T}R\\ A = \left( {{Q_1}^T{Q_2}^T} \right)R\\ A = \left( {{Q_1}{Q_2}} \right)R\\ \Rightarrow A = QR \end{array}Q2Q1A=RA=(Q2Q1)−1RA=(Q2Q1)TRA=(Q1TQ2T)RA=(Q1Q2)R⇒A=QR
Q=Q1Q2=(1323232313−2323−2313)(100022−220−2222)=(130−22323222623−2226)Q = {Q_1}{Q_2} = \left( {\begin{array}{ccc} {\frac{1}{3}}&{\frac{2}{3}}&{\frac{2}{3}}\\ {\frac{2}{3}}&{\frac{1}{3}}&{\frac{{ - 2}}{3}}\\ {\frac{2}{3}}&{\frac{{ - 2}}{3}}&{\frac{1}{3}} \end{array}} \right)\left( {\begin{array}{ccc} 1&0&0\\ 0&{\frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}\\ 0&{ - \frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 2 }}{2}} \end{array}} \right) = \left( {\begin{array}{ccc} {\frac{1}{3}}&0&{ - \frac{{2\sqrt 2 }}{3}}\\ {\frac{2}{3}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 2 }}{6}}\\ {\frac{2}{3}}&{ - \frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 2 }}{6}} \end{array}} \right)Q=Q1Q2=31323232313−2323−231100022−220−2222=313232022−22−3226262
最终通过Householder变换可以将矩阵分解为:A=QRA = QRA=QR,其中QQQ为对称的正交矩阵;RRR为对角非零的上三角矩阵。
相机模型的投影矩阵:
https://zhuanlan.zhihu.com/p/586364840





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








