长矩阵（宽矩阵）基于Householder变换的QR分解 Python源码

原创

已于 2023-09-21 14:05:18 修改 · 1.1k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #python #线性代数

于 2023-09-20 17:18:49 首次发布

本文介绍了如何使用Householder变换对非方阵进行QR分解，提供了一个Python代码示例，展示了如何处理长矩阵并生成正交矩阵Q和上三角矩阵R。

长矩阵（宽矩阵）基于Householder变换的QR分解 Python源码

前言
一、基于Householder变换的QR分解原理分析
二、Python源码
三、结果验证

前言

例题：随机产生一个11 * 8的实质矩阵A,并且分别实现基于Givens变换和Householder变换的QR分解
网上关于QR分解的讲解非常充分，但大多是对方阵进行的。本次例题作用于一个11 * 8的长矩阵的QR分解，查阅网上的代码发现Householder变换的代码在方阵变为长、宽矩阵时无法运行，故按照计算方式写一种计算方法。

一、基于Householder变换的QR分解原理分析

任何的实方阵都可以做QR分解：其中 Q 是正交阵， R 是上三角矩阵.。
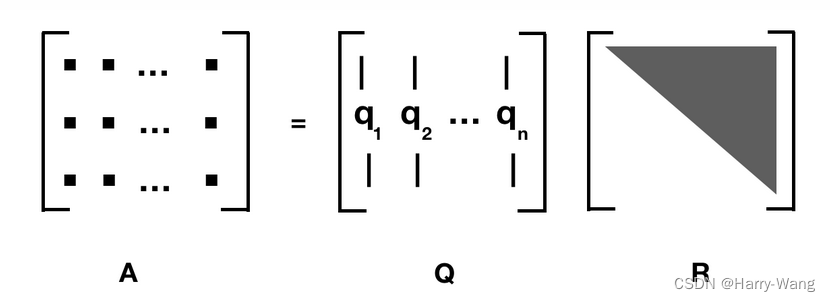
在这里插入图片描述
参考图片与原理详见

https://zhuanlan.zhihu.com/p/112327923
https://blog.youkuaiyun.com/m0_37604894/article/details/123360420

![在这里插入图片描述](https://img-blog.csdnimg.cn/289a7eb24ac84baa80c5b035f436298b.png
根据以上算法，在对实值矩阵A进行Householder变换时，按列依次计算

每次需要对矩阵一列进行反射变换，得到上三角矩阵的一列。
每次处理完一列，将处理好R矩阵第一行第一列去掉（可以使用矩阵切片操作），其余继续进行QR分解。
当R矩阵只剩1行或1列时，中止。
将每列的正交变换矩阵合在一起，得到最终的变换矩阵Q，R=Q逆乘A。

注：当实值矩阵不是方阵时（m * n），正交变换矩阵为方阵（m * m），左乘代表行变换。

二、Python源码

代码如下（示例）：

# 2.householder进行QR分解，并输出QR
import numpy as np
def qr_householder(A):
    h, l = A.shape  # h,l分别为输入矩阵的行数和列数
    q = np.identity(h)  # q矩阵h阶单位矩阵
    R = np.copy