神经网络中的优化算法

什么是优化算法？

给定一个具有参数θ的目标函数，我们想要找到一个θ使得目标函数取得最大值或最小值。优化算法就是帮助我们找到这个θ的算法。

在神经网络中，目标函数f就是预测值与标签的误差，我们希望找到一个θ使得f最小。

优化算法的种类

一阶优化算法

它通过计算目标函数f关于参数θ的梯度（一阶偏导数）来最小化代价函数。常用的SGD、Adam、RMSProp等基于梯度的优化算法都属于一阶优化算法。

梯度gradient与导数derivative的区别在于，前者用于多变量的目标函数，后者用于单变量的目标函数。

梯度可以用雅克比矩阵表示，矩阵中的每个元素代表函数对每个参数的一阶偏导数。

二阶优化算法

它通过计算目标函数f对参数θ的二阶偏导数来最小化代价函数。常用的有牛顿迭代法。

二阶偏导数可以用Hessian矩阵表示，每个元素都代表函数对每个参数的二阶偏导数。

对比

一阶优化算法只需要计算一阶偏导数，计算更容易
二阶优化算法虽然计算复杂，但是不容易陷入鞍点。

梯度下降法及其变种

在神经网络中，最常用的还是基于下面这种形式的梯度下降法（一阶优化算法）：

θ=θ−η⋅∇J(θ) 

η 为 learning rate
∇J(θ) 为 代价函数J(θ)对参数θ的梯度

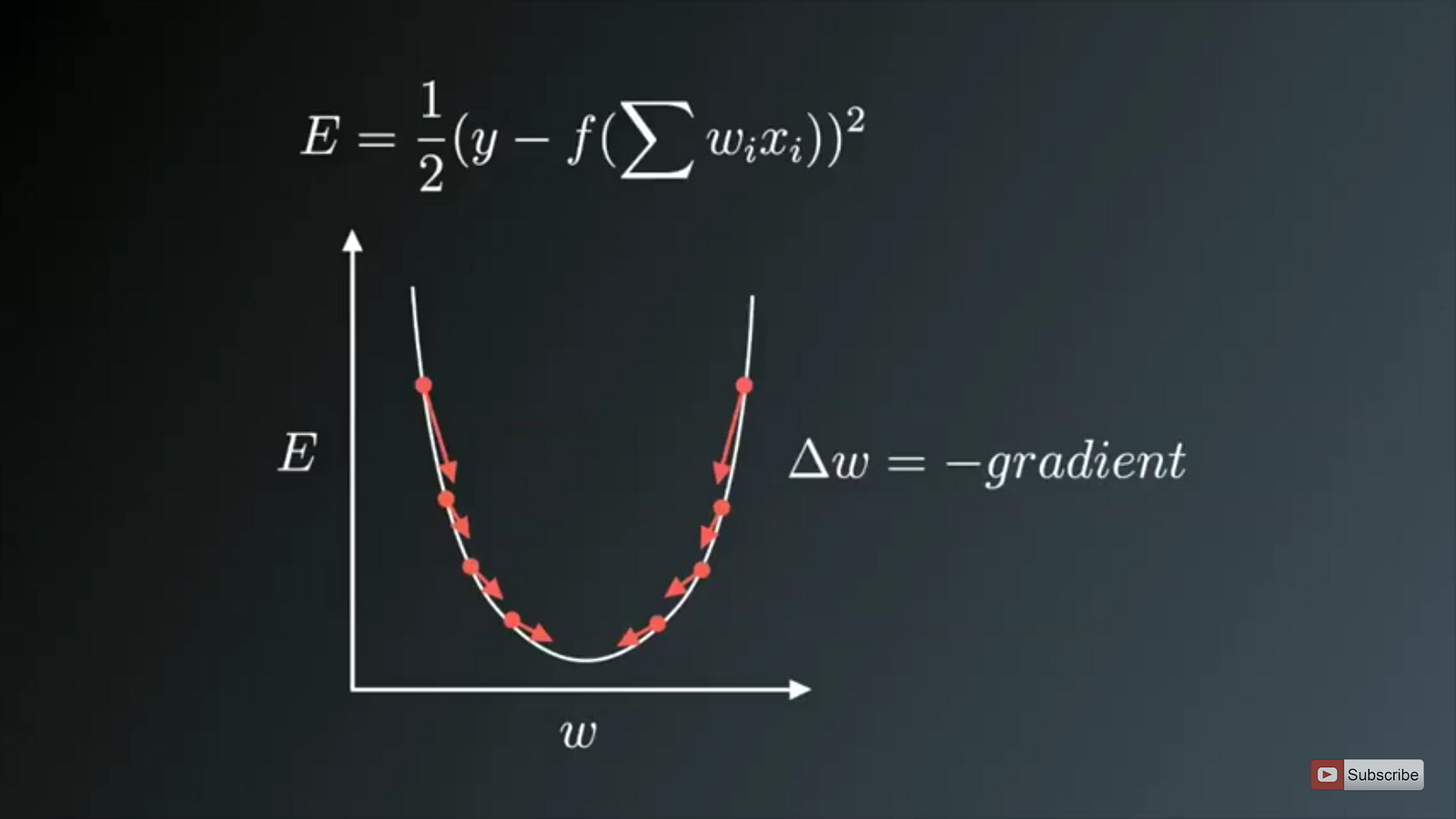
Batch gradient descent

一次参数的更新，需要所有样本都作为输入。样本量太大时容易一下子占满内存，而且不支持online update。

Stochastic gradient descent（SGD）

来一个样本，就执行一次参数更新，计算量大大减少，支持online update。缺点在于参数更新频率太高，参数波动较大，具有高方差（具体解释见文末）。如下图：

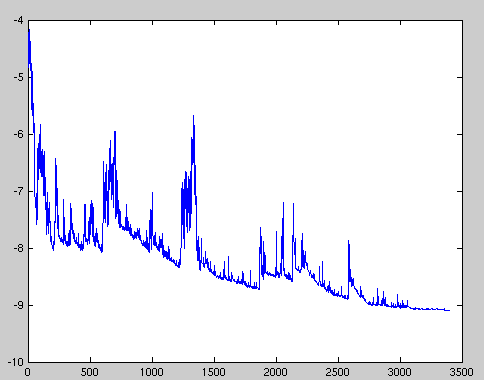
learning rate设置过大时容易使参数调节过度。因此使用时一定要保证learning rate不要太大。

Mini Batch Gradient Descent

前两种方法的折中，一次将一个mini batch（通常为50~256个样本）作为输入来执行一次参数更新。优点在于降低了参数更新的高方差；由于使用了mini batch，可以利用向量化编程来提高计算效率。
这是目前神经网络中最为常用的优化方法。

梯度下降法的升级版本

上面的几种方法都有一个共同的缺点：
1.对learning rate的设置较为敏感，太小则训练的太慢，太大则容易使目标函数发散掉。
2.针对不同的参数，learning rate都是一样的。这对于稀疏数据来说尤为不方便，因为我们更想对那些经常出现的数据采用较小的step size，而对于叫较为罕见的数据采用更大的step size。
3.梯度下降法的本质是寻找不动点（目标函数对参数的导数为0的点），而这种不动点通常包括三类：极大值、极小值、鞍点。高维非凸函数空间中存在大量的鞍点，使得梯度下降法极易陷入鞍点（saddle points）且长时间都出不来,如下左图：

注意：
陷入鞍点不代表真的不动了，有的梯度下降法比如SGD或NAG等可以在训练时间足够长后跳出鞍点。如下右图：

Momentum

这个方法是用来解决SGD的参数高幅震荡问题。加速参数在主要方向上的变化，减弱参数在非主要方向上的变化。
参数更新方式：

和共轭梯度法的作用类似，通过使用历史搜索方法对当前梯度方向的修正来抵消在非主要方向上的来回震荡。

SGD without momentum


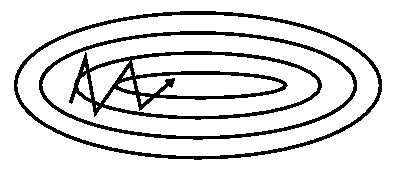
SGD with momentum

motentum方法的缺点主要在于，下坡的过程中动量越来越大，在最低点的速度太大了，可能又冲上坡导致错过极小点。

Nesterov accelerated gradient（NAG）

是对motentum算法进行的改进。给算法增加了预见能力，事先估计出下一个参数处的梯度，用于对当前计算的梯度进行校正。
参数更新：

首先沿上一次方向（γvt−1）跨出一大步(brown vector)，然后站在那儿计算一下梯度（∇θJ(θ−γvt−1)）(red vector)，于是，修正过的梯度方向就是γvt−1+η∇θJ(θ−γvt−1)(green vector)

而momentum方法呢？
首先在当前位置计算一下梯度（η∇θJ(θ)），（small blue vector），然后与上次的搜索方向（γvt−1）加起来，迈出了一大步（γvt−1+η∇θJ(θ)）（big blue vector）。

Adagrad

首次实现了adaptive learning rate adjustment。也就是不同参数具有不同的学习率。梯度大的参数补偿小一些，梯度小的参数步长大一些。
参数更新方式：
目标函数对每个参数的梯度：

gt,i=∇θJ(θi)

$$g_{t, i} = \nabla_\theta J( \theta_i )$$
不同于SGD：
$$\theta_{t+1, i} = \theta_{t, i} - \eta \cdot g_{t, i}$$
Adagrad通过分母项来达到不同参数具有不同学习率的目的：

θt+1,i=θt,i−ηGt,ii+ϵ−−−−−−−√⋅gt,