贪心 区间选点

题目

题目链接

分析

做法：将所有区间按照右端点排序，遍历所有的区间，如果区间的左端点严格大于上一次选的点则答案+1，否则跳过该区间。

证明：
假设最优解的个数为ans，以这种做法选出点的个数为cnt。(证明两个数a，b相等，可以分别证明：a >= b，a <= b)

• 1 证明ans <= cnt：ans为最优解，cnt为一种解，所以ans显然是小于等于cnt的。
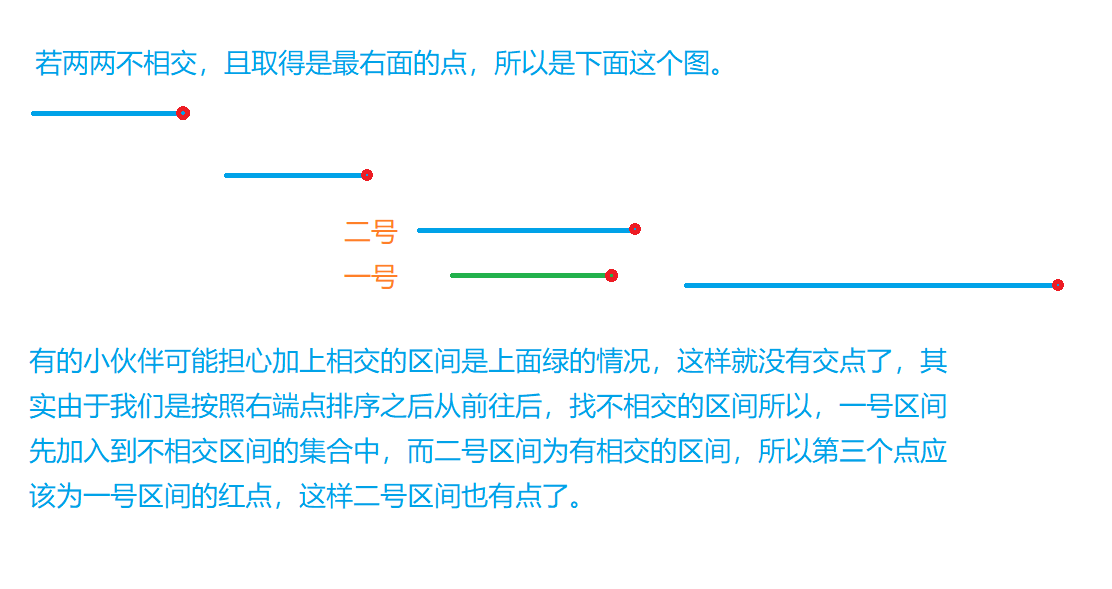
• 2 证明ans >= cnt：在一般问题中我们先看所有排完序后两两不相交的区间，假设总数为cnt，则按照这种算法需要cnt个点，然后再加上剩下的区间假设为n(n >= 0)个与上面区间相交的区间，需要加上num个点，num >= 0，取零是因为任意加上的区间与原本的区间相交(这里可能会有人有疑问，请看下面的图)，然后num上限就是无穷大。ans = cnt + num >= cnt。
• 由1、2得：ans = cnt

C++代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &obj) const
    {
        return r < obj.r;
    }
}range[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d%d", &range[i].l, &range[i].r);
    
    sort(range, range + n);
    
    int ans = 0, maxR = -2e9;
    for (int i = 0; i < n; i++)
        if (range[i].l > maxR) 
        {
            ans++;
            maxR = range[i].r;
        }
        
    printf("%d", ans);

    return 0;
}

参考

AcWing算法基础