低功耗电压可扩展算术单元设计

具有时序错误消除的低功耗电压可扩展算术单元设计

摘要

许多现有的供电电压过缩放(VOS)技术允许关键路径延迟增加，从而导致吞吐率降低。相反，不影响吞吐率的VOS技术会因时序错误而导致系统性能损失。本文提出了一种完美时序错误消除(PTEC)系统，该系统不仅保持了吞吐率，而且能够完全恢复系统性能。在输出位顺序计算的算术单元中，观察到由于VOS引起的时序违规发生在某些指定的最高位输出位上，从而导致输出值出现较大误差。利用这一特性，通过建模时序误差信号并推导出从受损信号中完全恢复的条件，提出了一种新颖的时序错误消除技术。所提出的PTEC系统通过 16×16无符号进位保存乘法器的设计实例进行了验证。仿真结果表明，与采用标称供电电压(=1V)的传统设计相比，所提出的PTEC系统在200mV过缩放下可实现38%的功耗降低，同时保持吞吐率和系统功能。

关键词

电压过缩放 ·时序错误恢复 ·低功耗算术单元 ·进位保存乘法器 ·算法噪声容限

1 引言

供电电压超缩放（VOS）是最高效的节能技术之一，因为数字电路的能量耗散与其供电电压（Vdd）呈二次关系[5,8,20,25]。然而，VOS的应用受限于数字电路的最坏情况延迟不得超过目标时钟周期，这为Vdd设定了下限。由于数字电路出现最坏情况延迟的概率并不高，因此严格遵守该时序约束的传统设计方法在功耗方面可能效率较低。

迄今为止，已提出多种电压超缩放（VOS）技术以缓解时序约束。文献 [9,18]的作者提出了利用时间借用技术来纠正由于VOS引起的时序错误的方法。在[10],中，开发了可伸展时钟技术以控制由VOS引起的时序错误。文献 [22,26]的作者应用前向纠错技术来纠正时序错误。在[2,6,12,13],中引入了近似计算技术，通过对数字操作进行近似以减少关键路径延迟，同时对功能行为影响较小。算法噪声容限（ANT）框架在[14]中被提出，可在算法层面消除时序误差。已有多种ANT技术被提出，应用于数字滤波[1,7,14,19,23],、图像/视频应用[16,21],以及数字通信应用[15,17]。尽管这些方案能有效消除时序错误，但输出结果仍包含未被ANT抑制的残余误差。因此，ANT技术主要针对那些设计用于满足特定算法服务质量（QOS）裕度的数字信号处理应用而开发。由于这种有误差的计算方式，ANT技术不适用于需要精确位计算的通用处理器中的算术逻辑单元（ALU）。对于依赖电池供电因而能量受限的高功耗嵌入式处理器，也需要在VOS条件下提供可靠操作结果的ALU。

因此，本文提出了一种新颖的错误恢复系统，该系统不仅能够在不降低系统吞吐量的情况下实现电压超缩放（VOS），而且还能保证从时序错误中实现完美重构，即一种完美时序错误消除（PTEC）系统。我们的方案可应用于输出位从最低有效位（LSB）到最高有效位（MSB）依次计算的算术逻辑单元（ALU），即所谓的最低有效位优先，最高有效位最后（LFML）算术单元。通过适当地控制Vdd，允许在某些指定的MSB处因VOS而产生时序错误。将这些时序误差视为加性噪声，所提出的系统能够准确地恢复这些时序误差，并从算术单元的噪声输出中将其消除。与先前的ANT方案[1,7,14–17,19,21,23]不同，本设计通过利用LFML‐based computation导致时序误差具有离散值这一特点，实现了精确的位级误差消除。特别值得将所提出的PTEC技术与[23]中的降低精度冗余（RPR）方法进行比较。RPR方法采用降低精度副本并替换当检测到时序错误时，目标单元的输出由复制单元替代。因此，期望输出无法被精确恢复。相反，所提出的PTEC方法直接从目标单元的输出中减去期望输出的精确估计值。最近，我们发现类似的思想已在[11]中独立提出。尽管本文与[11]中的工作都提出了实现完全误差补偿的方案，但我们的工作与之不同之处在于：我们为通用计算机中使用的算术单元提供了具体的完美误差校正设计（PEC design），而[11]中的工作主要关注用于数字信号处理（DSP）的单元，例如有限冲激响应滤波器（FIR filters）。具体而言，我们对乘法器架构的完全误差恢复条件进行了解析推导，并通过基于量化误差分析的PEC设计流程，证明了PEC系统在实现高能效乘法器方面的可行性。此外，我们还提出了针对错误校正单元的优化（最小延迟）硬件设计，该设计在[11]中尚未被提出。

使用所提出的PTEC技术，在预测技术模型（PTM）[4]中设计了算术逻辑单元中的关键组件二进制乘法器。在相同延迟和吞吐量条件下，当采用22纳米CMOS库设计时，PTEC系统可实现200毫伏电压超缩放，而不会引起任何时序错误，从而相比正常的Vdd(=1V)操作实现38%的节能。

本文的其余部分组织如下。在第2节中，研究了时序误差特性并建立了时序错误模型。第3节推导了电压超缩放下输出完美恢复的条件。基于该条件，详细描述了所提出的PTEC系统的设计，并以进位保存乘法器为例进行了说明。仿真结果与讨论见第4节。结论在第5节中给出。

2 时序误差的建模

在本小节中，我们提出由电压超缩放（VOS）引起的LFML算术单元的时序错误模型。当Vdd被缩放到低于保证正确电路操作的最小供电电压时，整体传播延迟可能超过时钟周期（Tc），从而导致某些输出位出现逻辑错误。考虑一个基于LFML计算的算术单元。由于最高有效位的传播延迟较大，时序错误将从最高有效位开始依次发生。在这种情况下，时序错误的可行范围可以通过控制电压缩放的程度来调节。在图1中，以进位保存乘法器为例详细说明了这一行为，其向量合并部分采用波纹进位加法器实现。设4 × 4为该乘法器第i个输出位的最坏情况传播延迟。由于该乘法器基于LFML计算，显然有τi> τj成立，其中i>j。当应用电压超缩放时，所有输出位的传播延迟都会增加。然后，输出位可分为两个组：一组最高有效位组满足 τi> Tc，另一组最低有效位组满足 τi ≤ Tc。最高有效位组因电压超缩放而暴露于时序错误之下，称为易错区域（EP区域），其余位则被称为安全区域。随着Vdd进一步激进地降低，易错区域扩大，因此更多的输出位会出现时序错误。

让我们考虑一种用于产生N位无符号输出位的LFML算术单元的时序错误模型。假设该算术单元的输出信号采用无符号格式。在电压超缩放场景下，该算术单元的第k个输出信号样本被分解为期望信号项和时序误差项，即

$$
z_k = y_k + e_k \quad (1)
$$

其中，$z_k$ 和 $y_k$ 分别是算术单元的噪声信号和理想输出信号，$e_k$ 是由电压超缩放引起的时序误差。由于 $e_k$ 可能具有负值，因此通过添加符号位为 $e_k$ 分配了 $(N+1)$ 位。将安全区域的位宽记为 $M$，误差信号 $e_k$ 的 $M$ 个最低有效位应为零。然后，我们得到

$$
e_k = [\ast \ast \cdots \ast \underbrace{\ast} {(N-M+1)\text{bits}} \underbrace{0 0 \cdots 0} {M\text{bits}}].
\quad (2)
$$

可以看出，信号$e_k$的值是 $2^M$的倍数，即$e_k = 2^M l$，其中整数$l \in [-2^{N-M} \cdots 2^{N-M} - 1]$。该时序错误模型用于设计所提出的PTEC系统，该系统能够完全消除时序误差。

3 PTEC系统设计

3.1 精确时序误差恢复条件

在本节中，我们提出了一种PTEC系统，该系统能够从（1）中的噪声输出$z_k$恢复理想的输出$y_k$。所提出的PTEC系统的框图如图2所示。近似处理单元（APU）利用减少的硬件资源来估计目标处理单元（TPU）的输出。误差校正单元（ECU）首先将记为 $\tilde{y}_k$的APU输出从噪声输出$z_k$中减去，从而得到

$$
v_k = z_k - \tilde{y}_k, \quad (3)
$$

然后估计表示为$\hat{e}_k$的时序误差，使用$v_k$。最后，从输出$z_k$中减去估计的时序误差，以恢复输出$\hat{y}_k$。如果实现了完全恢复，$\hat{y}_k$应与理想输出$y_k$完全相同。

由公式(1)和(3)可得

$$
v_k = e_k + (y_k - \tilde{y}_k), \quad (4)
$$

其中$(y_k-\tilde{y}_k)$称为“残差信号”。通过控制APU的精度，可以将残差信号$(y_k-\tilde{y}_k)$的幅度限制在一定范围内。注意，在LFML算术单元中，由于错误仅发生在EP区域，$e_k$的可能取值以 $2^M$为间隔分布，即$e_k = 2^M l$，其中整数$l \in [-2^{N-M} \cdots 2^{N-M}-1]$。如果残差信号的幅度被限定为 $B_l \leq (y_k - \tilde{y}_k) < B_h$ （或等价地，$e_k + B_l \leq v_k < e_k + B_h$）和

$$
(B_h - B_l) \leq 2^M, \quad (5)
$$

时序误差 $e_k$ 可以通过将观测值 $v_k$ 映射到满足 $2^M l + B_l \leq v_k < 2^M l + B_h$ 的点 $2^M l$ 来无歧义地恢复。图3展示了时序误差的精确恢复过程。由于每个 $e_k$ 实现所对应的 $v_k$ 范围互不重叠，因此可以确定产生结果 $v_k$ 的 $e_k$ 值。本质上，如果可能的残差信号 $(y_k - \tilde{y}_k)$ 的最大值与最小值之差小于 $2^M$，则可以从信号 $v_k$ 恢复时序误差 $e_k$。需要注意的是，如果 APU 的精度被选择为满足上述完全恢复条件，则来自 TPU 的时序错误可以被完美纠正。

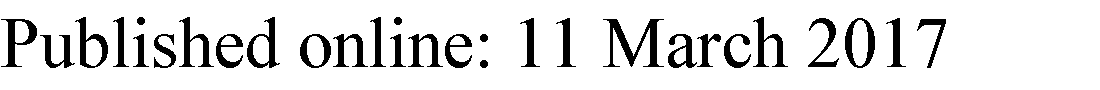
3.2 近似处理单元设计

在本节中，我们设计了所提出的PTEC系统中的近似处理单元（APU），以实现输出的完全恢复。基本上，APU与TPU具有相同的实现细节，只是APU的精度低于TPU。APU设计的目标是在满足(5)式的完全恢复条件的前提下，尽可能降低单元的位宽，从而减少面积复杂度，最小化PTEC系统的整体复杂度。

具体而言，通过选择APU的位宽，使得残差信号$(y_k−\tilde{y}_k)$ 的上限与下限$B_l$之差小于 $2^M$，以此满足完全恢复条件。因此，对于给定的供电电压，APU被通过以下方式设计：(1) 估算目标单元的安全区域的位宽$M$，基于路径延迟分析；(2) 推导出$(y_k - \tilde{y}_k)$作为位宽的函数关系；以及 (3) 选择满足(5) 的近似处理单元的最小位宽。

在本节中，以$L \times L$无符号进位保存乘法器为例，说明所提出的PTEC系统中近似处理单元的设计。设$a_k$和$b_k$为输入到目标乘法器的两个$L$位无符号数。然后，受时序误差影响的$N(= 2L)$位输出表示为

$$
z_k = a_k \times b_k + e_k, \quad (6)
$$

其中期望输出为$y_k = a_k \times b_k$。如果近似处理单元从目标乘法器的输入中取$P$个最高有效位（$P$ MSBs ($P < L$)），则我们有

$$
\tilde{y} k = (T {L-P}(a_k) \times T_{L-P}(b_k)), \quad (7)
$$

其中 $T_n(\cdot)$ 表示截断操作，丢弃最高到第 $n$ 位（例如，$T_2(11111) = 11100$）。

现在，目标是找到满足（P的最小值，该值满足（5）。

表示为$a_k = T_{L-P}(a_k)+\Delta a_k$ 和 $b_k = T_{L-P}(b_k)+\Delta b_k$，残差信号$(y_k - \tilde{y}_k)$ 表示为

$$
y_k - \tilde{y} k = a_k \times b_k - T {L-P}(a_k) \times T_{L-P}(b_k)
= (T_{L-P}(a_k)+\Delta a_k)\Delta b_k \underbrace{} {2L-P \text{ bits}} + \Delta a_k \times T {L-P}(b_k) \underbrace{}_{2L-P \text{ bits}}.
\quad (8)
$$

由(5)可知，$B_l = 0$和$B_h = 2^{2L-P+1}$，因为$(y_k - \tilde{y}_k)$位于$[0, 2^{2L-P+1} -1]$之间。因此，时序误差的精确恢复条件为

$$
2^{2L-P+1} \leq 2^M. \quad (9)
$$

因此，保证完全时序误差恢复的APU乘法器的最小精度被确定为

$$
P = 2L - M + 1. \quad (10)
$$

所提出的近似处理单元设计可通过简单降低精确处理单元的精度并计算出实现完全恢复的合适位宽，从而应用于任何LFML算术单元设计。让我们考虑二进制补码有符号乘法器，其中$a_k$和$b_k$是$L$位有符号数，其最高有效位用作符号位。在这种情况下，式((yk − ˜yk)8)中的残差信号并不总是正数，因此式(9)的精确恢复条件不再成立。我们可以通过修改式(7)来使残差信号为正：

$$
\tilde{y} k = (T {L-P}(a_k) + \text{sign}(a_k)2^{L-P+1}) \times (T_{L-P}(b_k) + \text{sign}(b_k)2^{L-P+1}), \quad (11)
$$

其中 $\text{sign}(x)$ 在 $x < 0$ 时输出 $1$，否则输出 $0$。注意，该操作等价于将 $a_k$ 和 $b_k$ 的符号位相加后输入到近似处理单元（APU）（见图4）。然后，上述描述的错误校正步骤可以不做任何修改地使用，就像 TPU 是一个无符号乘法器一样。由于对 APU 的修改仅需要 $P$ 个半加器，因此功耗的增加预计非常有限。

3.3 错误校正单元的设计

在本节中，设计了ECU以从$\hat{e}_k$和$z_k$以及 $\tilde{y}_k$中估计错误，如图2中虚线框所示。首先，将APU的输出从TPU的输出中减去，得到$v_k$，如公式(3)所示。然后，从$e_k$中估计时序误差

$$
\hat{e}_k = 2^M l \quad \text{such that} \quad {2^M l \leq v_k < 2^M(l+1)}. \quad (12)
$$

注意，(12) 可以通过截断操作简单实现为

$$
\hat{e}_k = T_M(v_k). \quad (13)
$$

最后，从噪声输出 $z_k$ 中减去时序误差的估计值 $\hat{e}_k$，即

$$
\hat{y}_k = z_k - \hat{e}_k. \quad (14)
$$

由于时序误差的估计是精确的，即$\hat{e}_k = e_k$，因此可以完美地获得期望信号而没有任何退化，也就是说，$\hat{y}_k = y_k$。将(3)和(13)代入(14)，我们得到

$$
\hat{y}_k = z_k - T_M(z_k - \tilde{y}_k), \quad (15)
$$

该式描述了误差校正单元（ECU）的操作。(15)式的直接计算需要进行$(2L - 2P)$位的减法运算以得到$v_k = z_k - \tilde{y}_k$，以及另一次$(2L - M)$位的减法运算以得到 $z_k - T_M(v_k)$，当$M$较小时会引入显著的传播延迟。这种较长的传播延迟是不希望出现的，因为它会叠加到目标乘法器中获取安全区域位所需的传播延迟上，从而限制了电压缩放的程度。为了找到具有更短传播延迟的ECU结构，将(15)式中构成$\hat{y}_k$的位分为两部分：$M$个最低有效位记为$\hat{y}^{(LSB)}_k$，以及$(2L - M)$个最高有效位记为$\hat{y}^{(MSB)}_k$。类似地，将$z_k$中的位也划分为$z^{(LSB)}_k$和$z^{(MSB)}_k$。显然，由于$(z_k - \tilde{y}_k)$的低$M$位在(15)式中被截断，因此$\hat{y}^{(LSB)}_k$与$z^{(LSB)}_k$相同。另一方面，$\hat{y}^{(MSB)}_k$由下式给出

$$
\hat{y}^{(MSB)}_k = z^{(MSB)}_k - ((z_k - \tilde{y}_k) \gg M) \quad (16)
$$

其中

$$
(z_k - \tilde{y}_k) \gg M =
\begin{cases}
z^{(MSB)}_k - (\tilde{y}_k \gg M) & \text{if } z^{(LSB)}_k \geq \tilde{y}^{(LSB)}, \
z^{(MSB)}_k - (\tilde{y}_k \gg M) - 1, & \text{if } z^{(LSB)}_k < \tilde{y}^{(LSB)}.
\end{cases}
\quad (17)
$$

由(16)和(17)可得，$\hat{y}_k = [\hat{y}^{(LSB)}_k,\hat{y}^{(MSB)}_k]$

$$
\hat{y}^{(LSB)}_k = z^{(LSB)}_k
$$

$$
\hat{y}^{(MSB)}_k =
\begin{cases}
(\tilde{y}_k \gg M), & \text{if } z^{(LSB)}_k \geq \tilde{y}^{(LSB)}, \
(\tilde{y}_k \gg M)+ 1, & \text{if } z^{(LSB)}_k < \tilde{y}^{(LSB)}.
\end{cases}
\quad (18)
$$

3.4 通用PTEC框架在其他算术单元中的应用

到目前为止，我们已经介绍了$L \times L$进位保存乘法器示例的PTEC技术设计。PTEC技术可应用于基于LFML计算的各种计算架构。在本小节中，我们将描述如何将PTEC原理应用于通用的基于最低有效位优先、最高有效位最后的算术单元。从原始供电电压开始，我们考虑以步长（例如，步长= 0.1V）逐步降低供电电压。对于给定的供电电压，我们可以通过硬件仿真分析输出位的最坏情况路径延迟。由于基于最低有效位优先、最高有效位最后的计算方式，最高有效位的路径延迟会高于低位。因此，通过硬件仿真识别出路径延迟小于时钟周期并留有适当裕度的输出位，即可确定安全区域的位宽$M$。一旦$M$确定后，我们需要找到近似处理单元的最佳精度$P$，使得式（5）中的完全误差恢复条件得到满足。具体而言，需要确保残差信号（即TPU和APU输出之间的差异）的上界$B_h$与下界$B_l$之间的差值小于$2^M$。对于给定的精确处理单元架构，我们可以解析地推导出残差信号的上界$B_h$和下界$B_l$作为精度$P$的函数（例如，

$$
B_l = 0, B_h = 2^{2L-P+1}
$$

对于前几小节中描述的示例）。然后，我们可以在满足约束条件$(B_h - B_l) \leq 2^M$的前提下，找到最小的精度$P$。一旦确定了$P$，我们需要设计执行图3所示功能映射的误差校正单元。当精确处理单元的精度降低以获得近似处理单元时，我们可以使用公式(13)中的简单截断操作来实现误差校正单元。最后，我们估算精确处理单元、近似处理单元和误差校正单元模块的功耗，并针对每个供电电压值保存相应的功耗数据。我们重复上述过程，直到供电电压无法进一步降低为止，因为此时已不存在满足完全误差恢复条件的有效$P$值。

最后一步，我们通过选择实现最小功耗的设计，来确定基于PTEC的算术单元的最佳设计。下面我们总结设计PTEC系统的详细步骤和指导原则：

– 步骤1：从原始供电电压开始，将供电电压降低一步（例如，步长为= 0.5 V）。
– 步骤2：通过硬件仿真分析每个输出位的路径延迟，并找出对应于安全区域位宽的$M$值。
– 步骤3：通过分析APU中的量化效应，计算残差信号的上界$B_l$和下界$B_h$。$(y_k - \tilde{y}_k)$
– 步骤4：寻找满足(5)式中完全误差恢复条件的最小APU精度$P$。如果该APU精度不可行，则转至步骤7。
– 步骤5：设计执行(15)式操作的ECU硬件。
– 步骤6：评估总功耗并保存结果，返回步骤1。
– 步骤7：比较所有尝试过的供电电压下的功耗，选择最优的一个。

请注意，上述设计流程不仅限于一个示例，还可扩展到基于LFML计算的通用算术单元。此类算术单元的输出最高有效位路径延迟较大。因此，通过硬件仿真，我们可以确定安全区域的位宽$M$，其路径延迟小于时钟周期。无论使用何种算术单元，均采用式（5）中的完全误差恢复条件来确定APU的精度$P$。对于给定的TPU/APU结构，我们只需进行适当的量化误差分析，以推导出上界$B_h$和下界$B_l$。尽管实际的硬件实现可根据不同架构稍作调整，但ECU在式（13）中的基本功能映射对通用算术单元而言是相同的。本质上，PTEC设计方法可应用于各种基于LFML的算术操作，例如进位保留加法器、华莱士树乘法器[24],以及Baugh–Wooley乘法器[3]，仅需对$B_h$和$B_l$的量化分析及ECU硬件实现进行轻微修改即可。

4 结果与讨论

在本节中，采用PTM和22 nm CMOS工艺库设计了$L \times L$无符号进位保存乘法器。在整个研究工作中，假设系统共享一个共同的$V_{dd}$，因为对TPU和APU使用不同的$V_{dd}$会由于引入电平转换器和额外的电源调节器而产生显著的功耗和面积开销。进行HSPICE仿真以获得传播延迟随目标电源电压$V_{dd}$的变化关系。首先，我们为$L = 16$设计所提出的PTEC系统。考虑到原始乘法器在标称$V_{dd}(=1V)$下的关键路径延迟，目标时钟频率设定为2.5 GHz。其中包含10%的裕度，以考虑触发器的建立时间以及由片内工艺变化、抖动、老化等因素引起的一些变化。$V_{dd}$调节的最小步长设为100 mV。对于每个$V_{dd}$，利用通过HSPICE仿真获得的延迟模型计算安全区域的位宽$M$。在这些计算中，包含了由于错误校正单元 $\tau_{\text{additional}} (= \tau_{FA} + \tau_{mux})$带来的额外计算延迟。考虑到建立时间及上述各种因素的影响随着 $V_{dd}$调节而增加，我们为较低的$V_{dd}$设置15%的延迟裕量$(= \tau_{\text{margin}})$。然后，确定满足条件的最大$M$值

$$
\tau_{\text{safe}} + \tau_{\text{additional}} + \tau_{\text{margin}} < T_c \quad (19)
$$

被找到，其中$\tau_{\text{safe}}$是生成安全区域位所需的关键路径延迟，而$T_c$是时钟周期。注意，在此计算中，要求APU的关键路径延迟以及式(18)中加1操作的延迟小于 $\tau_{\text{safe}}$。如果该条件不成立，则关键路径延迟将超过 $\tau_{\text{safe}} + \tau_{\text{additional}} + \tau_{\text{margin}}$（进而超过$T_c$）。因此，为了PTEC系统的正常运行，需增加一个额外约束，即APU的传播延迟必须小于 $\tau_{\text{safe}}$。如果满足该约束，则PTEC系统的关键路径延迟由式(19)中的左侧项给出。

表1 安全区域的位宽和APU的精度随供电电压的变化
| 供电电压 | 1.0伏特 | 0.9伏特 | 0.8伏特 |
| — | — | — | — |
| $M$ | N/A | 26 | 23 |
| $P$ (APU精度) | N/A | 7 | 10 |

表2 门数量与供电电压
| 供电电压 | 1.0伏特 | 0.9伏特 | 0.8伏特 |
| — | — | — | — |
| 目标处理单元 AND | 256 | 241 | 220 |
| FA | 240 | 225 | 204 |
| HA | 32 | 26 | 23 |
| 近似处理单元 AND | N/A | 49 | 100 |
| FA | N/A | 42 | 90 |
| HA | N/A | 14 | 20 |
| 错误校正单元 FA | N/A | 8 | 11 |
| HA | N/A | 6 | 9 |
| MUX | N/A | 6 | 9 |

图6显示了关键路径延迟随供电电压$V_{dd}$变化的仿真结果。如图6所示，只要$V_{dd}$大于或等于800mV，时序约束即被满足。然而，当供电电压低于800 mV时，由于精度提高，APU的传播延迟显著增大，导致违反我们的要求。这为所提出的PTEC系统中$V_{dd}$的电压缩放设置了下限。注意，随着$V_{dd}$的降低，TPU的关键路径延迟并不会增加，因为TPU的处理在安全区域内前$M$个最低有效位计算完成后即结束（见图5）。由于这些$M$位满足时序约束，因此TPU的总延迟不应超过时钟周期，如图6所示。表1显示了在此下限下的$M$和$P$的估计结果。一旦$M$确定，APU的精度$P$即可通过公式(10)进行估计。每种$V_{dd}$所需的逻辑门数量总结于表2。注意，虽然APU的门数量随着$V_{dd}$的降低而增加，但TPU的门数量却减少，因为用于计算易错位的冗余电路随着$V_{dd}$的缩放而增长。用于时序误差校正的额外硬件可能会给整个系统带来额外负载。例如，如图5所示，输入信号的某些位同时馈送到TPU和APU，这会引入额外负载。然而，当输入驱动器紧邻TPU输入端放置时，APU带来的额外负载对目标单元的关键路径延迟影响较小。显然，这会导致输入驱动器与APU输入逻辑门之间的互连变长。请注意，我们在仿真中已建模了此类互连延迟。

所提出的PTEC系统的功能行为也已进行了仿真和验证。使用从 HSPICE仿真中获得的逻辑延迟，针对随机生成的1000个测试输入，获得了 16×16无符号进位保存乘法器的时序误差。图7显示了所提出的

的时域波形)

PTEC系统在$V_{dd}$为900毫伏时。7 a–d展示了期望输出$y_k$、时序误差$e_k$、恢复信号$\hat{y} k$以及重构误差$(y_k - \hat{y}_k)$在$V {dd} = 900$ mV下的时域波形，分别对应。由图7 d可知，所提出的PTEC系统完美消除了时序误差。

表3 PTEC方案在$L=16$和 $24$下的设计规格与节能
| $L$ | 电源电压（毫伏） | $M$ | $P$ | 节能百分比 |
| — | — | — | — | — |
| 16 | 800 | 23 | 10 | 62 |
| 24 | 800 | 35 | 14 | 59 |
| 32 | 800 | 48 | 16 | 57 |

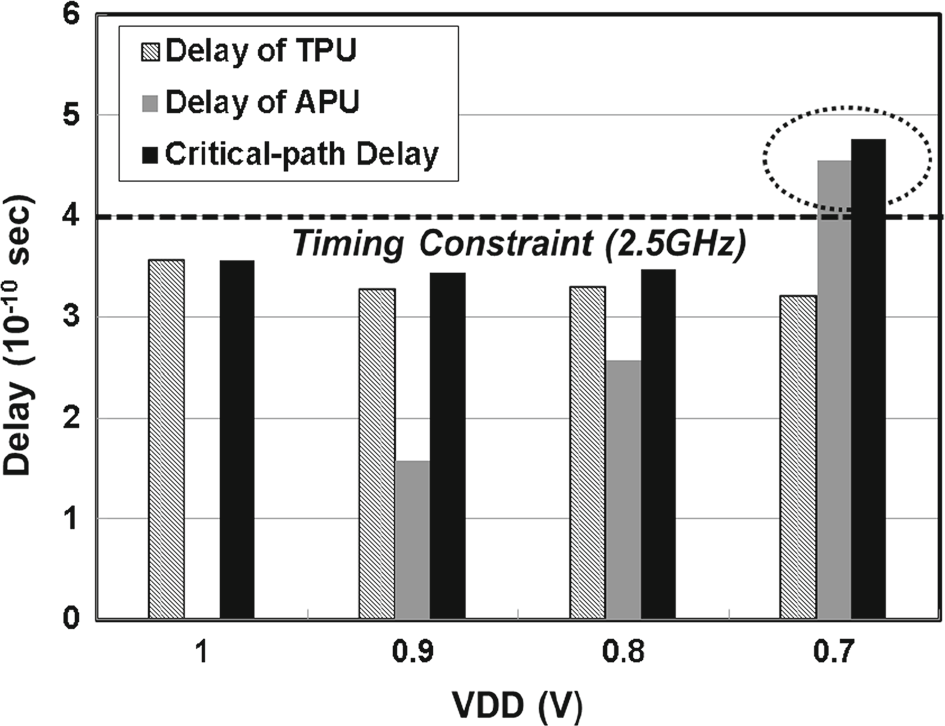
图8显示了基于所提出的PTEC的 16 × 16无符号进位保存乘法器的功耗，该数据来自HSPICE功率仿真。结果相对于未进行电压缩放的传统乘法器所消耗的功耗进行了归一化。可以观察到，随着供电电压$V_{dd}$的降低，TPU的功耗迅速下降。可以看出，功耗的下降速度远快于理论预期，即功耗与$\sim V_{dd}^2$成正比。这似乎是由于动态漏电和短路功耗（占总功耗的相当大比例）减少，以及TPU中逻辑门数量随$V_{dd}$的缩放而减少所致。当$V_{dd}$降低时，APU的功耗增加，因为安全区域的位宽$M$减小，因此根据公式(10)中APU的精度变高。尽管如此，我们知道通过电压超缩放可以实现显著的整体功耗节省。如图8所示，与未采用VOS的原始乘法器相比，所提出的设计在$V_{dd} = 900$和800毫伏下分别实现了19%和38%的节能。文献[14]中的ANT方案在输出信噪比超过 20 dB时仅提供有限的节能效果。此外，ANT方案无法实现输出信号的完美恢复。然而，所提出的PTEC系统不仅能够实现输出信号的完全恢复，还能带来显著的节能效果。

接下来，我们评估PTEC技术在具有更大位宽的乘法器上的性能，即$L = 24$和 32。对于每个$L$值，近似处理单元都会被重新设计使得式(10)中的完全恢复条件得到满足，并且供电电压被确定为满足式(19)中的时序约束。表3总结了针对每个$L$值的PTEC技术的设计规格。表中还包含了PTEC方案所实现的节能效果。对于所有考虑的情况，我们无法将供电电压降低到800毫伏以下，以免违反式(19)的时序约束。我们观察到，当精确处理单元的位宽增大时，所提出的乘法器仍能保持显著的节能效果。注意，PTEC技术对于 32 × 32无符号乘法器最多可实现57%的节能。

5 结论

在本文中，我们提出了一种新颖的系统，能够从电压过缩放引起的时序误差中完全恢复输出样本。通过利用最低有效位优先和最高有效位最后计算的算术单元中时序误差的内在特性，推导出了实现完全恢复的条件。采用16 × 16进位保存乘法器验证了所提出的PTEC系统。仿真结果表明，在使用PTM和 22纳米CMOS库的情况下，可在无重构误差的前提下实现显著的节能效果。因此，所提出的PTEC系统预计将在能量受限但需要容错算术的通用处理器或嵌入式处理器中算术逻辑单元的设计中具有重要应用价值。