基于模糊山峰聚类的Web使用模式发现
摘要
对电子商务组织的Web服务器日志进行分析,对于深入了解用户的Web使用行为至关重要,这有助于设计最具吸引力的网站。本文提出了一种基于山峰密度函数(MDF)的模糊聚类框架,用于从网络日志中发现用户会话簇。该框架的主要步骤包括网络日志预处理、基于MDF的用户会话簇发现及其验证。为应对用户会话高维性的问题,提出了一种为用户会话赋权的模糊方法。在用户会话簇发现方面,探讨了模糊C均值(FCM)和模糊C中心点(FCMed)算法。由于选择合适的初始聚类中心是一个重大挑战,本文提出了基于MDF的模糊C均值(MDFCM)和模糊C中心点(MDFCMed)算法以解决此问题。实验结果表明,使用MDFCM/MDFCMed形成的聚类质量明显优于FCM和FCMed。
关键词 :模糊聚类;山峰密度函数;MDF;模糊聚类验证;用户会话聚类。
1 引言
万维网作为巨大的信息来源,是应用数据挖掘原理的沃土。Web使用挖掘被描述为从用户与网站上的网络资源进行交互所产生的数据中自动发现使用模式的过程(莫巴舍尔,2007)。所发现的模式通常表示为一组网络资源,这些资源被具有共同兴趣的用户群体频繁访问(卡莫纳等,2012)。聚类算法已被广泛应用于发现代表相似URL访问模式的用户会话簇。这些提取出的聚类基于用户的共同导航行为来表示其访问模式。安萨里等(2011a,2011c)提出了一种使用硬聚类算法进行Web会话数据聚类的框架。
由于不同网络用户的交互行为和非确定性浏览模式,用户会话数据可能不完整,或包含噪声和异常值。这类数据具有模糊性和不确定性,缺乏清晰边界,并且常常出现重叠聚类(周等,2006)。对用户会话数据进行模糊聚类时,将每个用户会话划分到多个聚类中,每个用户会话可以以不同的隶属度属于多个聚类,从而使聚类能够自然地形成其应有的形状。
最常用的模糊聚类技术之一是模糊C均值(FCM)(贝兹戴克,1981),它进行模糊聚类的方式是使给定对象可以以由隶属度等级指定的隶属度属于多个聚类。另一种称为模糊C中心点(FCMed)算法(克里斯纳普拉姆等,2001)的模糊聚类算法通过引入模糊集合概念来扩展硬c中心点算法,从而生成模糊聚类(梅和陈,2011)。每个聚类由一个作为该聚类中心点的代表对象表示。
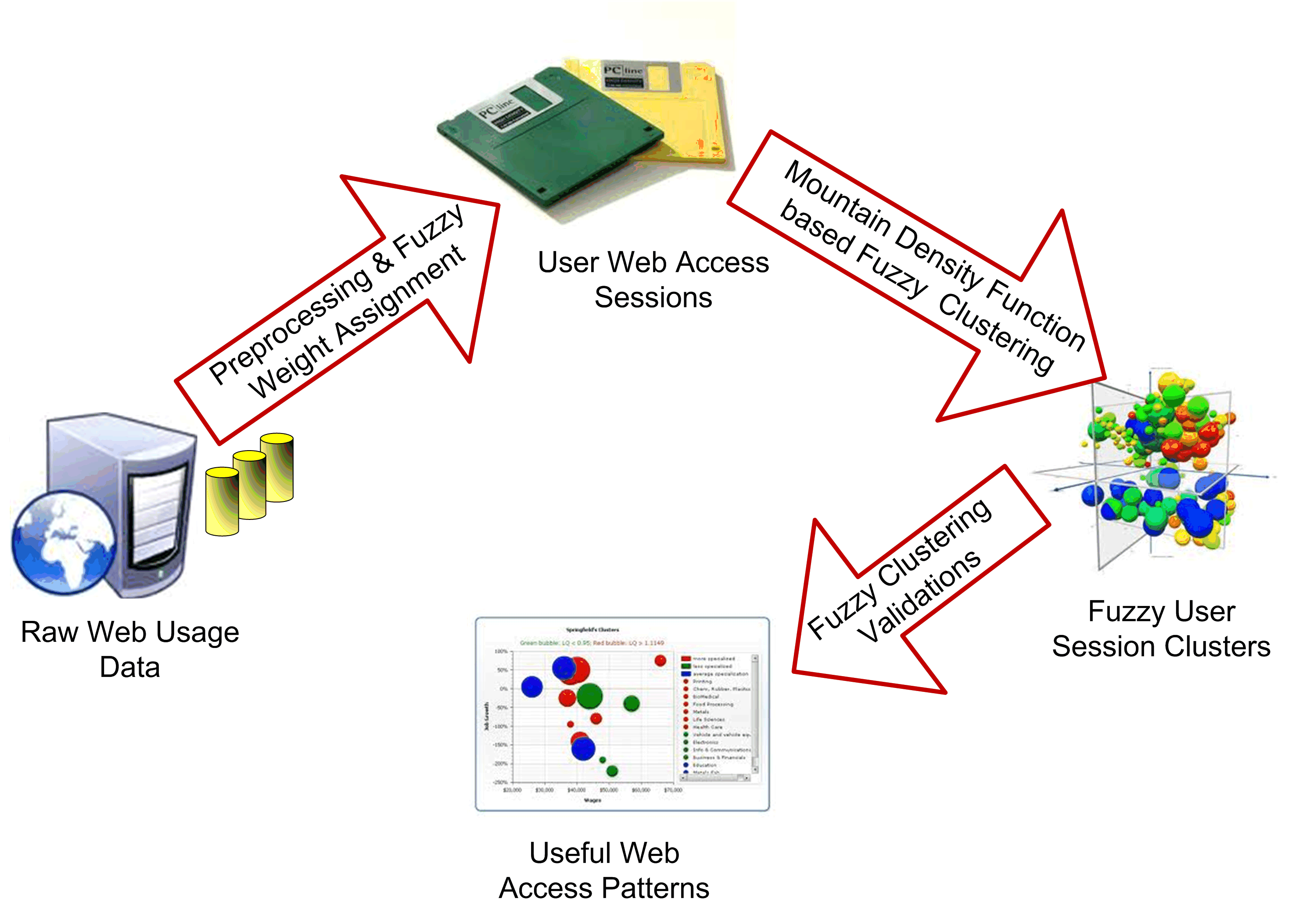
FCM和FCMed方法的一个主要问题是它们对初始聚类中心的选择敏感。因此,估计合适的初始聚类中心值是这些方法面临的一大挑战。本文提出了一种基于山峰密度函数(MDF)的初始化策略,以找到合适的初始聚类中心集合。文中提出了一个用户会话聚类框架,该框架将MDF聚类中心初始化集成到FCM和FCMed算法中。图1展示了所提出框架的整体结构。该框架包含三个主要步骤:
- Web日志数据预处理和对用户会话的模糊权重分配
- 使用基于MDF的模糊聚类技术进行用户会话簇发现
- 发现聚类的验证。
本文的其余部分组织如下。在第2节中,我们简要讨论了网络日志预处理、用户会话表示以及为用户会话分配模糊权重的方法。第3节详细描述了所提出的基于MDF的模糊用户会话聚类框架及其底层数学模型。第4节讨论了用于评估发现的模糊聚类质量的有效性指数。第5节展示了实验结果及相关讨论。最后,第6节给出了结论。
2 用户会话提取和模糊权重分配
为了将无标签的、半结构化的文本原始网络日志数据转换为一组数值型用户会话向量,必须进行网络日志预处理。预处理利用多种算法和启发式技术来执行各项任务,如数据清洗、用户识别和会话识别等。安萨里等人(2011b,2011d)已提供了用于预处理网络日志数据的各种技术的详细信息。每个提取出的用户会话向量都记录了该用户会话期间访问的一组网址,如2.1小节所述。2.2小节简要描述了基于线性和标准S模糊隶属函数的模糊集理论方法,用于为用户会话及其会话中访问的页面网址分配权重。
2.1 用户会话的表示
设 $ s_1, s_2, \ldots, s_m $ 为预处理网络日志后发现的用户会话集合。设 $ u_1, u_2, \ldots, u_n $ 为预处理日志中出现的所有网址的集合。其中,$ m $ 和 $ n $ 分别为发现的用户会话数量和预处理网络日志中出现的网址总数。每个用户会话是在一个n维空间中的URL值向量。一个用户会话 $ s_i $ 如(1)式所示:
$$
s_i = {u_{i1}, u_{i2}, \ldots, u_{in}}, \quad i = 1, 2, \ldots, m
$$
其中每个 $ u_{ik} $ 表示第 $ i $ 个用户会话中第 $ k $ 个URL的访问状态。所有用户会话可以以下列矩阵形式表示:
$$
\begin{pmatrix}
u_{11} & u_{12} & \cdots & u_{1n} \
u_{21} & u_{22} & \cdots & u_{2n} \
\vdots & \vdots & \ddots & \vdots \
u_{m1} & u_{m2} & \cdots & u_{mn}
\end{pmatrix}
$$
2.2 用于URL和会话权重分配的模糊方法
通过移除低支持度网址(即未达到指定用户会话数量支持的网址)的引用,对Web访问日志进行过滤,可以在提高聚类结果的同时提供一种有效的降维方法。为此,根据各网址的用户会话支持次数(即访问特定网址的用户会话数量),使用隶属函数为其分配模糊权重。所有会话支持次数低于下限 $ \alpha_1 $ 的网址被赋予权重0;而所有会话支持次数高于上限 $ \alpha_2 $ 的网址则被赋予权重1。对于会话支持次数介于 $ \alpha_1 $ 和 $ \alpha_2 $ 之间的其余网址项目,则使用模糊隶属函数赋予0到1之间的权重。我们采用线性模糊隶属函数(LFMF)和标准S模糊隶属函数(SFMF)为不同的URL项目分配权重。设 $ x $ 为网址 $ u_k $ 的会话支持次数,则 $ \omega_{u_k} $ 分配给该网址 $ u_k $ 的基于LFMF的权重通过以下方式计算:
$$
\omega_{u_k} =
\begin{cases}
0, & \text{if } x \leq \alpha_1 \
\frac{x - \alpha_1}{\alpha_2 - \alpha_1}, & \text{if } \alpha_1 < x < \alpha_2 \
1, & \text{if } x \geq \alpha_2
\end{cases}
$$
使用以下方法计算分配给 URL $ u_k $ 的基于 SFMF 的权重:
$$
\omega_{u_k} =
\begin{cases}
0, & \text{if } x \leq \alpha_1 \
2\left(\frac{x - \alpha_1}{\alpha_2 - \alpha_1}\right)^2, & \text{if } \alpha_1 \leq x \leq x_0 \
1 - 2\left(\frac{x - \alpha_2}{\alpha_2 - \alpha_1}\right)^2, & \text{if } x_0 \leq x \leq \alpha_2 \
1, & \text{if } x \geq \alpha_2
\end{cases}
$$
其中 $ x_0 = (\alpha_1 + \alpha_2)/2 $ 是交叉点。
由于非常小的会话可能代表数据中的噪声,因此使用基于会话访问的网址数量的模糊隶属函数为所有会话分配权重。设 $ \beta_1 $ 和 $ \beta_2 $ 分别为会话网址数量的下限和上限阈值,$ y = |s_i| $ 表示用户会话 $ s_i $ 中访问的网址数量,则基于LFMF和SFMF的权重 $ \omega_{s_i} $ 被分配给用户会话 $ s_i $,分别通过替换公式(3)和(4)的修改版本来计算,即将 $ \omega_{u_k} $ 替换为 $ \omega_{s_i} $,$ \alpha_1 $ 替换为 $ \beta_1 $,$ \alpha_2 $ 替换为 $ \beta_2 $,$ x $ 替换为 $ y $,以及 $ x_0 $ 替换为 $ y_0 $,其中 $ y_0 = (\beta_1 + \beta_2)/2 $ 为交叉点。
3 模糊用户会话簇发现
设 $ {v_j | j = 1, \ldots, c} $ 表示代表 $ {g_j | j = 1, \ldots, c} $ 中每个c个聚类的聚类中心的一组n维向量。其中 $ v_j = (v_{j1}, v_{j2}, \ldots, v_{jn}) $,$ j = 1, \ldots, c $。其中 $ v_{jk} $ 表示第 $ j $ 个聚类中心的第 $ k $ 个 URL 属性值。令 $ \mu_{ij} $ 表示用户会话 $ s_i $ 在聚类 $ g_j $ 中的隶属度,其中 $ \mu_{ij} \in [0,1], \forall i = 1,\ldots,m, \forall j = 1,\ldots,c $。
$ m \times c $ 模糊划分矩阵 $ [\mu_{ij}] $ 描述了用户会话向量在各个聚类中的分配,需满足以下约束条件:
$$
\sum_{j=1}^{c} \mu_{ij} = 1, \quad \forall i = 1,\ldots,m
$$
$$
0 < \sum_{i=1}^{m} \mu_{ij} < m, \quad \forall j = 1,\ldots,c
$$
以下小节描述了FCM、FCMed以及所提出的基于MDF的模糊用户会话聚类技术的算法细节。
3.1 基于FCM的用户会话聚类
FCM算法结合了模糊集理论概念中的部分隶属思想,能够形成重叠聚类。基于FCM的用户会话聚类的目标函数 $ J_{FCM} $ 是用户会话与其聚类中心之间距离的加权和,如公式(7)所述。
$$
J_{FCM} = \sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}^q |s_i - v_j|^2
$$
其中 $ |s_i - v_j|^2 $ 表示用户会话 $ s_i $ 与聚类中心 $ v_j $ 之间的欧几里得距离。当未对用户会话和网址分配权重时,欧几里得距离 $ |s_i - v_j|^2 $ 通过以下方式计算:
$$
|s_i - v_j|^2 = \sum_{k=1}^{n} (s_{ik} - v_{jk})^2
$$
如果为用户会话和网址分配模糊权重,则使用以下公式计算 $ |s_i - v_j|^2 $:
$$
|s_i - v_j|^2 = \sum_{k=1}^{n} w_{s_i} w_{u_k} (s_{ik} - v_{jk})^2
$$
其中,$ w_{s_i} $ 是分配给用户会话 $ s_i $ 的模糊权重,而 $ w_{u_k} $ 是分配给第 $ k $ 个 URL 的模糊权重。通过交替更新用户会话对各个聚类的成员等级并重新计算聚类中心,直至收敛,从而实现目标函数 $ J_{FCM} $ 值的最小化。在每次迭代过程中,使用(10)更新聚类中心。
$$
v_j = \frac{\sum_{i=1}^{m} \mu_{ij}^q s_i}{\sum_{i=1}^{m} \mu_{ij}^q}
$$
模糊划分矩阵 $ [\mu_{ij}] $ 使用(11)进行更新:
$$
\mu_{ij} = \frac{1}{\sum_{l=1}^{c} \left( \frac{|s_i - v_j|}{|s_i - v_l|} \right)^{2/(q-1)}}
$$
算法1 描述了基于FCM的用户会话聚类所涉及的步骤。
3.2 基于FCMed的用户会话聚类
在FCMed聚类方法中,每个聚类由一个代表性的用户会话对象表示,该对象称为该聚类的中心点(乔希和克里希纳普拉姆,2000)。设 $ {d_j | j = 1, \ldots, c} $ 是表示 $ {g_j | j = 1, \ldots, c} $ 中每个c个聚类对应的n维聚类中心点向量的集合。这里,$ D $ 是用户会话集合的一个子集。
其中 $ d_j = (d_{j1}, d_{j2}, \ldots, d_{jn}), j = 1, \ldots, c $,其中 $ d_{jk} $ 表示第 $ k $ 个 URL 属性值对应的第 $ j $ 个聚类中心点。该 $ m \times c $ 模糊划分矩阵 $ [\mu_{ij}] $ 可以按照 FCM算法 中定义的方式进行填充:
$$
\mu_{ij} = \frac{1}{\sum_{l=1}^{c} \left( \frac{|s_i - d_j|}{|s_i - d_l|} \right)^{2/(q-1)}}
$$
新的聚类中心点可以使用以下方法计算:
$$
d_j = \arg\min_{s_p \in D} \sum_{i=1}^{m} \mu_{ij}^q |s_i - s_p|^2
$$
算法2 描述了基于FCMed的用户会话聚类算法所涉及的步骤。
3.3 MDFCM和基于MDFCMed的用户会话聚类
在所提出的MDFCM和MDFCMed算法中,通过计算每个用户会话的MDF值来选择初始聚类中心。具有最高MDF值的用户会话被选为第一个初始聚类中心。后续的初始聚类中心通过迭代消除先前选定的聚类中心的影响并修正MDF值得到。设 $ S = {s_1, s_2, \ldots, s_m} $ 为n维欧几里得空间中的m个用户会话的集合。为了确定第一个初始聚类中心,将每个用户会话 $ s_i $ 视为一个潜在候选,并计算在用户会话 $ s_i $ 处的第一个MDF值,记为 $ h_1(s_i) $,其计算公式如下:
$$
h_1(s_i) = \sum_{k=1}^{m} \exp\left(-\frac{|s_i - s_k|^2}{\sigma^2}\right), \quad i = 1, \ldots, m
$$
其中 $ \sigma $ 是一个正数常量,用于定义用户会话 $ s_i $ 的邻域。用户会话 $ s_i $ 的MDF值是其附近所有用户会话密度的近似值。超出径向距离的用户会话对其MDF值影响较小。
具有最高MDF值的用户会话被选为第一个聚类中心 $ v_1 $,如下所示:
$$
v_1 = \arg\max_{s_i \in S} h_1(s_i)
$$
基于模糊山峰聚类的Web使用模式发现
3 模糊用户会话簇发现(续)
在选择第二个聚类中心时,为了降低第一个聚类中心周围的MDF值对各用户会话的影响,需修订每个用户会话的MDF值,如下所示:
$$
h_2(s_i) = h_1(s_i) - h_1(v_1) \exp\left(-\frac{|s_i - v_1|^2}{\sigma^2}\right), \quad i = 1, \ldots, m
$$
在修正所有用户会话的MDF值后,选择具有最高MDF值的作为第二个聚类中心,如下所示:
$$
v_2 = \arg\max_{s_i \in S} h_2(s_i)
$$
同样,对于第 $ j $ 个聚类中心的选择,每个用户会话的MDF值将按如下方式进行修订:
$$
h_j(s_i) = h_{j-1}(s_i) - h_{j-1}(v_{j-1}) \exp\left(-\frac{|s_i - v_{j-1}|^2}{\sigma^2}\right), \quad i = 1, \ldots, m
$$
且第 $ j $ 个聚类中心 $ v_j $ 按如下方式选择:
$$
v_j = \arg\max_{s_i \in S} h_j(s_i)
$$
算法3 描述了基于MDFCM的用户会话聚类所涉及的步骤。类似地,通过将算法1的步骤1替换为算法3的步骤1至10,可得到基于MDFCMed的用户会话聚类的算法。
算法3 基于MDFCM的用户会话聚类
输入 :$ c $,邻域半径 $ \sigma $,误差阈值 $ \varepsilon $,最大迭代次数 $ \eta $ 以及用户会话集合 $ {s_1, \ldots, s_m} $
输出 :$ c $ 个聚类中心的集合 $ {v_1, \ldots, v_c} $ 和划分矩阵 $ [\mu_{ij}] $
- 对于 $ i \leftarrow 1, m $ do
- 计算山峰值 $ h_1(s_i) $ 使用(14)
- 结束循环
- 使用(15)计算第一个聚类中心 $ v_1^{(0)} $
- 对于 $ j \leftarrow 2, c $,执行
- 对于 $ i \leftarrow 1, m $ do
- 计算修正后的山峰值 $ h_j(s_i) $ 使用(18)
- 结束循环
- 使用(19)计算第 $ j $ 个聚类中心 $ v_j^{(0)} $
- 结束循环
- $ t \leftarrow 1 $
-
重复
- 计算划分矩阵 $ [\mu_{ij}(t)] $ 项:- 对于 $ i \leftarrow 1, m $ do
- 对于 $ j \leftarrow 1, c $ 执行
- 使用(11)计算 $ \mu_{ij}(t) $
- 结束循环
-
结束循环
- 计算新聚类中心的集合 $ {v_j(t)} $: - 对于 $ j \leftarrow 1, c $,执行
- 使用(10)计算 $ v_j(t) $
- 结束循环
- 使用(7)计算目标函数 $ J_{FCM}(t) $
- $ t \leftarrow t+1 $
- 直到 $ |J_{FCM}(t) - J_{FCM}(t-1)| < \varepsilon $ 或 $ t > \eta $
4 模糊聚类有效性评估
本节介绍了本研究中用于评估发现的模糊聚类质量的质量度量方法。
4.1 夏-边尼(XB)指数
夏边尼(XB)有效性指数(夏和边尼,1987年)定义如下:
$$
XB = \frac{\sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}^q |s_i - v_j|^2}{m \cdot \delta_{\min}^2}
$$
其中 $ \delta_{\min}^2 $ 是如下给出的聚类中心之间最小欧几里得距离的平方:
$$
\delta_{\min}^2 = \min_{1 \leq l,k \leq c, l \neq k} |v_l - v_k|^2
$$
较小的XB指数值表示紧凑且分离良好的聚类。
4.2 福山-菅野(FS)指数
福山‐铃木(FS指数)(福山,1989年)定义为:
$$
FS = \sum_{i=1}^{m} \sum_{j=1}^{c} \mu_{ij}^q |s_i - v_j|^2 - \sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}^q |v_j - v|^2
$$
其中 $ v $ 是所有聚类中心向量的均值:
$$
v = \frac{1}{c} \sum_{j=1}^{c} v_j
$$
对于紧凑且分离良好的聚类,期望的 FS 指数值较小。
4.3 Zahid分离(SC)紧凑性有效性指数
SC 指数(Limouri等人,1999年)定义为:
$$
SC = 1 - \frac{C}{S}
$$
其中
$$
C = \frac{\sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}^q |s_i - v_j|^2}{\sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}}
$$
and
$$
S = \frac{\sum_{j=1}^{c} \sum_{k=j+1}^{c} \sum_{i=1}^{m} \sum_{i=1}^{m} \mu_{ij} \mu_{ik} |v_j - v_k|^2}{\max_{1 \leq x \leq c} \sum_{i=1}^{m} \mu_{ix}}
$$
较大的SC指数值表明簇内凝聚性良好且簇间重叠较小。
4.4 误差指数
误差指数表示模糊用户会话聚类的目标函数,定义如下:
$$
\text{Error Index} = \sum_{j=1}^{c} \sum_{i=1}^{m} \mu_{ij}^q |s_i - v_j|^2
$$
误差指数的值越低,表示聚类结果越好。
5 实验结果与讨论
输入的Web访问日志取自一个大学校园的代理服务器。这些Web访问日志覆盖了一周期间,从2008年6月1日到2008年6月8日。总共包含723,263个网络日志请求。我们使用Perl脚本来分离出与Google网站相关的请求。提取出的针对Google资源的网络日志请求数量为12,744。
5.1 网络日志数据预处理结果
表1显示了预处理结果。在执行清理后,网络日志包含11,567项。日志文件中识别出的用户总数为30。用户会话通过基于时间的启发式方法进行识别。
| 项 | |
|---|---|
| 初始日志条目数 | 12,744 |
| 清理后的日志条目数 | 11,567 |
| 识别的用户数 | 30 |
| 访问的URL数量 | 116 |
| 已识别的用户会话 | 319 |
为了给用户会话分配模糊权重,将会话网址数量的下限 $ \beta_1 $ 设为1,上限 $ \beta_2 $ 设为4。表2显示了对用户会话分配模糊权重的结果。
| URL数量 | 会话数量 | 会话权重 LFMF | 会话权重 SFMF |
|---|---|---|---|
| 4+ | 91 | 1 | 1 |
| 4 | 4 | 0.75 | 0.875 |
| 3 | 32 | 0.5 | 0.5 |
| 2 | 54 | 0.25 | 0.125 |
| 1 | 212 | 0 | 0 |
5.2 模糊用户会话聚类结果
实验过程的详细信息如下:
- 对FCM、FCMed、MDFCM和基于MDFCMed的用户会话聚类算法进行了多次运行
- 对于上述算法的每次运行,计算XB、FS、SC和误差聚类有效性指数
- 对于上述算法的每次运行,使用以下类型的输入用户会话:
1. 无权重的用户会话
2. 基于LFMF权重的用户会话
3. 基于SFMF权重的用户会话
- 采用以下参数设置:
1. 簇数量 $ c $,从2变化到50
2. 模糊指数 $ q $ 设置为2
3. 误差阈值 $ \varepsilon $ 设置为0.01
4. 最大迭代次数 $ \eta $ 设置为100
5. 邻域半径 $ \sigma $ 设置为 $ \sqrt{n} $
5.3 FCM 与 MDFCM 的比较
图2描绘了通过应用FCM和基于MDFCM的用户会话聚类所发现的用户会话簇的各种模糊有效性指数的值。图2(a)显示了XB指数得分随簇数量的变化情况。该指数的值越小,表示聚类质量越好,具有更高的簇内紧凑性和簇间分离度。从图中可以非常清楚地看出,对于不同簇数量值,MDFCM算法形成的模糊聚类质量明显优于FCM算法所发现的聚类质量。图2(b)描述了FS指数得分随簇数量的变化情况。由于FS指数表示簇内紧凑性与簇间分离度之间的差异,因此该指数值越低,代表聚类质量越好。从图中明显可以看出,相较于FCM算法在不同簇数量值下所发现的聚类,基于MDFCM的用户会话聚类在FS指数方面得到了质量更优的聚类结果。图2(c)提供了SC指数值随簇数量的变化情况。该指数值越高,表示模糊聚类质量越好。该图清楚地表明,相较于FCM算法在不同簇数量值下所发现的聚类,基于MDFCM的用户会话聚类在SC指数方面产生了更高品质的聚类。图2(d)显示了模糊聚类误差指数得分随簇数量的变化情况。该指数值越小,表示模糊聚类误差越小,聚类质量越好。该图清楚地表明,使用基于MDFCM的用户会话聚类所产生的模糊聚类误差比使用FCM算法更小。聚类质量得以提升的主要原因是通过采用基于MDF的初始化策略,对初始聚类中心进行了更为合理的选择。
5.4 FCMed与MDFCMed比较
图3提供了应用MDFCMed和FCMed算法发现的用户会话簇的各种有效性指数值。图3(a)、3(b)、3(c)和3(d)明确表明(原因与图2的解释相同),在XB、FS、SC和误差有效性指数方面,使用所提出的MDFCMed算法发现的模糊聚类的质量明显优于FCMed算法。
5.5 时间性能比较
图4(a)和(b)展示了FCM和MDFCM对用户会话进行聚类时,执行时间随簇数量变化的曲线图,分别对应不使用和使用基于LFNF的权重的情况。从这些图中可以明显看出,所提出的MDFCM算法的执行时间略优于FCM算法。图4(c)和图4(d)描绘了对用户会话进行FCMed和MDFCMed聚类时,执行时间与簇数量的关系图,其中用户会话分别未分配和分配了基于LFNF的权重。从这些图中可以明显看出,所提出的MDFCMed的执行时间略优于FCMed算法。
5.6 使用和不使用会话权重的MDFCM
图5给出了应用所提出的MDFCM算法发现的用户会话簇在不同簇数量下的各种模糊聚类有效性指数的值。图5(a)、5(b)、5(c)和5(d)清楚地表明,使用基于权重的模糊用户会话所形成的模糊聚类在XB、FS、SC和误差有效性指数方面优于未使用会话权重的聚类质量。此外,使用LFMF和基于SFMS的权重的用户会话所形成的聚类质量彼此相当。
6 结论
本文提出了一种基于MDF的模糊聚类框架,旨在从Web使用数据中发现Web用户会话簇,以提高所提取聚类的质量。本工作在Web使用聚类发现方面的贡献是:
- 为了有效发现用户会话簇,探索了FCM和FCMed聚类技术,并给出了使用这些算法进行用户会话聚类的数学表述。
- 为了解决初始聚类中心选择的问题(该问题在形成高质量聚类中起着至关重要的作用),提出了基于MDF的MDFCM和MDFCMed算法,并给出了其数学和算法细节。
- 提出了一种模糊集理论方法,用于为用户会话及相关网址分配模糊权重,以应对包含噪声和异常值(表现为无关紧要的会话和网址)的高维用户会话数据。模糊权重分配使用LFMF和SFMF模糊隶属函数来完成。
上述算法已实现,并通过使用各种模糊聚类有效性指数(如XB、FS、SC和误差指数)进行了多个实验,以评估其有效性和性能。
根据本研究进行的各项实验所获得的结果,可以得出以下结论:
1. 实验结果明确表明,MDFCM和MDFCMed算法能够有效识别合适的初始聚类中心,从而在XB、FS、SC及误差指数等多种模糊聚类指数方面形成质量更优的模糊聚类。
2. 所提出的MDFCM和MDFCMed算法的时间性能分别略优于或相当于FCM和FCMed算法。尽管计算MDF值会带来额外的计算成本,但时间性能提升的主要原因是基于MDF的初始聚类中心选择使得这些算法收敛更快,尤其是在簇数量较多时,从而减少了整体聚类时间。
3. 对用户会话和URL项目的模糊权重分配已被发现能够从XB、FS、SC和误差指数方面提高MDFCM和MDFCMed-based user session clustering的聚类性能和质量。这表明模糊权重分配很好地实现了减少无关紧要的用户会话和网址所带来的负面影响的目的,从而形成了质量改进的聚类。




















 1478
1478

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








