【深度学习初探】Day04 - 神经网络_神经网络推测小强是否去看电影plotpc-优快云博客

本文链接：https://blog.youkuaiyun.com/oo00Z00oo/article/details/129959062

【深度学习初探】Day04 - 神经网络

文章目录

【深度学习初探】Day04 - 神经网络
1.1 从感知机到神经网络
1.2 激活函数
2.1 多维数组的运算
2.2 3层神经网络的实现
- 2.2.1 符号确认
- 2.2.2 各层间信号传递的实现
2.3 输出层的设计
3.1 手写数字识别

1.1 从感知机到神经网络

神经网络和感知机有很多共同点。感知机虽然有处理复杂函数的可能性，但是设定权重的工作——确定合适的、能符合预期的输入与输出的权重，现在还是由人工进行。因此神经网络出现了，它可以自动地从数据中学习到合适的权重参数。现在，我们以两者的差异为中心，介绍神经网络的结构。

1.1.1 神经网络的示例

用图来表示神经网络，如图1所示。
在这里插入图片描述
我们把最左边的一列叫做输入层，把中间的一列叫做中间层，有时候也叫隐藏层（意思是肉眼看不见），最右边的一列叫做输出层。图中的网络一共由3层神经元构成，但实质上只有2层神经元有权重，所以我们把它称为2层网络。

1.1.2 明确表示偏置b的感知机

在Day04的学习中，我们学习了感知机的构成，并引入了权重和偏置，将感知机总结为如下式所示：
在这里插入图片描述
b是被称为偏置，用于控制神经元被激活容易程度的参数；而w1和w2是表示各个信号的权重的参数，用于控制各个信号的重要性。如果要在感知机的表示图中明确表示出 b ，可以像下图那样，增设一个输入信号1，将权重值设为 b 。至此，这个感知机将 x1、x2、1 三个信号作为神经元的输入，和各自权重 w1、w2、b 相乘后，传送到下一个神经元。
在这里插入图片描述
现在，是时候将感知机用更简洁的形式表示了。权重和信号相乘后传送到下一个神经元，由下一个神经元计算这些加权信号的总和。如果这个总和超过 0，则输出 1，否则输出 0 。我们把这种判断动作设为函数 h（x）。将前式改成下面的式子：
在这里插入图片描述

h（x）判断传入参数的值，如果 ≤ 0，就返回 0；如果＞ 0，就返回 1 。

1.1.3 激活函数的出现

        其实，1.1.2中的 h（x)，它会将输入信号的总和转换为输出信号，这种函数我们一般称为激活函数（activation function）。激活函数的作用在于决定如何来激活输入信号的总和。
        下面，我们进一步细分公式，表示出激活函数计算的过程。
在这里插入图片描述
        将偏置和加权输入信号的总和记为 a ，然后代入 h（x）函数，赋给 y 。表示出来就是下图的样子：

神经元用一个⚪来表示。

1.2 激活函数

当一个激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为阶跃函数。因此，可以说感知机使用了阶跃函数作为激活函数。如果将激活函数从阶跃函数换成其他函数，会怎样呢？这才是进入神经网络世界的基本。

1.2.1 sigmoid函数

神经网络中经常使用的一个激活函数就是sigmoid函数（sigmoid function）。
在这里插入图片描述
其中，exp（-x）表示 e^(-x)。看似复杂，其实它也仅仅是个函数而已。一个输入的x，对应一个输出的y。比如h（1.0）= 0.731…、h（2.0） = 0.880…
神经网络中经常用sigmoid函数作为激活函数，下面，我们通过sigmoid函数和阶跃函数的比较来学习sigmoid函数、

1.2.2 阶跃函数的实现

阶跃函数的实现倒是很简单，当输入超过0时，输出1，否则输出0。就如下：

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

这个实现简单、易于理解，但是参数x只能接受实数（浮点数），不允许NumPy数组作为参数，下面，我们把它修改为支持传入NumPy数组。

def step_function(x):
    y = x > 0
    return y.astype(np.int)

虽然只有两行，但是初看根本看不懂。我们用一个实例来示范一下：

x = np.array([-1.0, 1.0, 2.0])
y = x > 0
print(y)

输出：

[False True True]

看到这输出，我们才明白，原来NumPy里的不等式有返回值，x > 0 会返回一个布尔类型的np.array，内容是：x里大于0的元素变成True，小于0的变为False。如此，y是一个布尔类型的元素组成的np.array。但是感知机返回的数据应该是1或0，所以我们调用了astype(np.int)函数，将bool转换为了int。这就是NumPy使用的技巧。

1.2.3 绘制阶跃函数的图形

使用matplotlib库，绘制阶跃函数图形。

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    return np.array(x > 0,dtype=np.int_)

x = np.arange(-5.0, 5.0, 0.1)    # 在-5.0到5.0范围内，以0.1为单位，生成NumPy数组([-5.0,-4.9,...,4.9])
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)             # 指定y轴展示的范围为-0.1~1.1
plt.show()

输出：
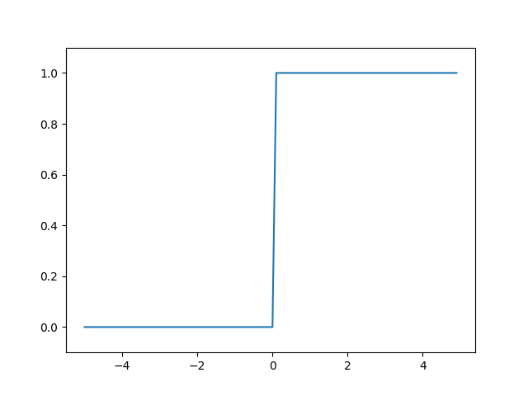
在这里插入图片描述
如图，阶跃函数以0为界，输出从0跃迁到了1，它的值呈阶梯式变化。

1.2.4 sigmoid函数的实现

sigmoid函数要实现也不难，如下：

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

这里np.exp(-x)就是e^(-x)。而且这个函数也支持NumPy数组，因为你调用的是np.exp( )函数，不是普通的函数，而借助于NumPy的广播功能，1 / np.array( ) 也会将标量 1 与数组各个元素进行运算。

t = np.array([1.0, 2.0, 3.0])
print(1.0 + t)
print(1.0 / t)

输出：

[2. 3. 4.]
[1. 0.5 0.33333333]

接下来，我们把sigmoid函数也画在图上，如下图：

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

输出：
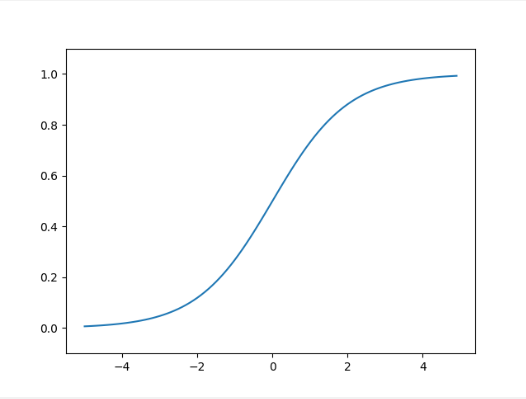
在这里插入图片描述

1.2.5 sigmoid函数和阶跃函数的比较

        现在我们来比较一下sigmoid函数和阶跃函数。
        首先注意到的是“平滑性”不同，sigmoid函数是随着输入发生连续性变化的平滑曲线，而阶跃函数是以0为界，输出发生急剧变化。sigmoid函数的平滑性，对神经网络学习有重要意义。
        另一个重要区别，阶跃函数不是输出0就是输出1，而sigmoid函数可以返回任何实数，也就是说，感知机中神经元间流动的是0/1二元信号，而神经网络中流动的是连续的实数值信号。但是，两者的结构均为”输入越小，输出越接近0；输入越大，输出越接近1，不管输入信号有多小或多大，输出信号的值都在0到1之间。

1.2.6 非线性函数

实际上，阶跃函数和sigmoid函数，两者均为非线性函数，一条是曲线，一条是阶梯一样的折线。神经网络的激活函数必须使用非线性函数，换句话说，激活函数不能使用线性函数。
线性函数的问题在于，不论如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。假如有一个线性函数 h (x) = cx 作为了激活函数，把 y(x) = h(h(h(x))) 作为三层神经网络。那么这个运算会进行 y(x) = c × c × c × x 的乘法运算，但是同样的处理可由y(x) = ax (a=c^3)来表示，如此，多层隐藏层神经网络就失去了意义，因此激活函数必须使用非线性函数。

1.2.7 ReLU函数（Rectified Linear Unit）

        sigmoid很早就开始被使用了，但最近主要使用的激活函数是RELU函数。
        RELU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。
        RELU函数可以表示为下面的式子：
在这里插入图片描述
        RELU函数是一个非常简单的函数。因此，它的实现也非常简单，我们在Python中，通过两行就能实现：

def relu(x):
    return np.maximum(0 , x)

其中NumPy的maximum函数会从两个参数中选择较大的值输出。现在，我们照例输出RELU函数的图像：

x = np.arange(-0.5,0.6,0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-0.1,1.1)
plt.show()

输出：
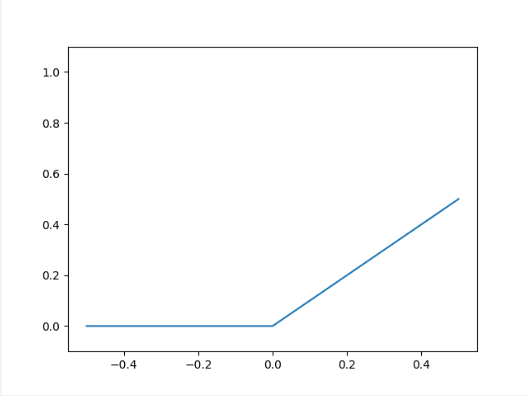
在这里插入图片描述

2.1 多维数组的运算

NumPy多维数组的运算帮助高效实现神经网络。

2.1.1 多维数组

多维数组是“数字”的集合，数字排成一列、一个长方形、一个三维形状甚至N维状的集合都叫多维数组。下面我们用NumPy来生成多维数组，先从一维数组开始。

import numpy as np
A = np.array([1, 2, 3, 4])
print(A)
print(np.ndim(A))
print(A.shape)
print(A.shape[0])

输出：

[1 2 3 4]
1
(4,)
4

我们建立了一个一维数组，通过 np.dim( ) 函数取得了它的维数，值为1。
又用实例变量 shape 取得了它的形状。注意，A.shape 的结果是一个元组（tuple)，np.ndim(A) 返回元组（4, ）表示 A 有4个元素。这里返回元组的原因是，二维数组和三维以上数组必须以元组形式返回，比如（4，3），表示4行3列，为了保证返回值类型一致，所以一维数组也返回一个元组。
我们使用 A.shape[0] 下标索引输出了该元组的第一个元素：4。

下面，我们再生成一个二维数组：

B = np.array([[1, 2],[3, 4],[5, 6]])
print(B)
print(np.ndim(B))
print(B.shape)

输出：

[[1 2]
[3 4]
[5 6]]
2
(3, 2)

这里生成了一个3 × 2 数组B。它的第一维度（行）有3个元素，第二维度（列）有两个元素。在NumPy中，第一个维度叫成第0维，第二个维度叫成第1维。二维数组也叫矩阵（matrix）。横向排列叫行（row），纵向排列叫列（column）。

2.1.2 矩阵乘法

NumPy的矩阵乘法和我们所学的线性代数里的运算方法一致，如图：
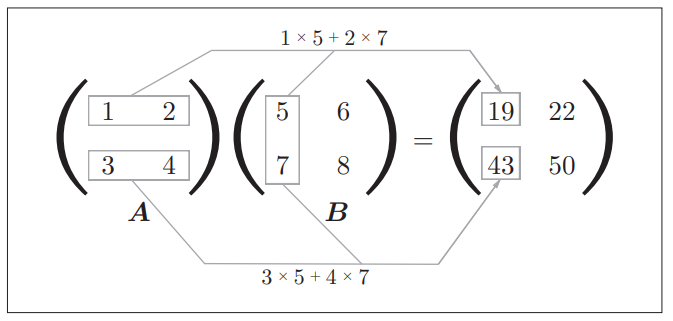
在这里插入图片描述
在Python中用代码实现：

A = np.array([[1, 2],[3, 4]])
print(A.shape)
B = np.array([[5, 6],[7, 8]])
print(B.shape)
print(np.dot(A, B))

输出：

(2, 2)
(2, 2)
[[19 22]
[43 50]]

调用 np.dot( )，接收两个NumPy数组作为参数，返回数组的矩阵乘积。要注意，np.dot(A, B)和np.dot(B, A)的值可能不一样，因为这是矩阵相乘。矩阵相乘前，要注意两个矩阵的形状，矩阵A的列数必须和矩阵B的行数相等，才可以相乘。
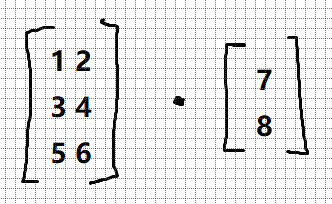
在这里插入图片描述
但是如果矩阵B是一个一维数组，它的元素个数仍要保持一致的原则。意思是A有两列，B也要有两个元素。

A = np.array([[1, 2],[3, 4],[5, 6]])
print(A.shape)
B = np.array([7, 8])
print(B.shape)
print(np.dot(A, B))

输出：

(3, 2)
(2,)
[23 53 83]

这个时候B的两个元素是排成列来被A所乘的。
在这里插入图片描述

2.1.3 神经网络的内积

神经网络的某一层计算，在Python中可以用NumPy矩阵的内积进行计算。假设有这样一个神经网络，只有一层权重：
在这里插入图片描述
这个神经网络省略了偏置和激活函数，只有权重。现在应该是：

x1 * w1 +x2 * w2 = y1，
x1 * w3 + x2 * w4 = y2，
x1 * w5 + x2 * w6 = y3。

如何用Python的NumPy数组实现呢？我们创建几个矩阵。

X = np.array([1, 2])
print(X)
W = np.array([[1, 3, 5],[2, 4, 6]])
print(W)
Y = np.dot(X, W)
print(Y)

就这么简单，使用多维数组的点积，就可以直接一次算出一层的神经传感。即便Y的元素个数为100或1000，也可以通过一次运算就计算出。
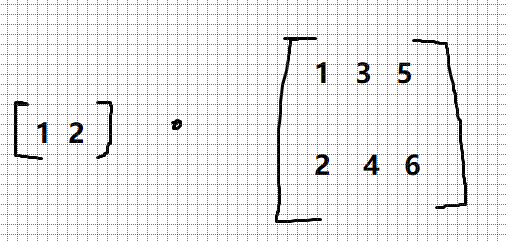
在这里插入图片描述

2.2 3层神经网络的实现

3层神经网络，从输入到输出的（前向）处理，使用NumPy数组，可以用很少的代码完成神经网络的前向处理。
在这里插入图片描述
3层神经网络：输入层（第0层）有2个神经元，第1个隐藏层（第1层）有3个神经元，第2个隐藏层（第2层）有2个神经元，输出层（第3层）有2个神经元。

2.2.1 符号确认

在使用Python编写3层神经网络前，我们要先明确一些符号，比如 w12(1)、a1(1) 等符号。如下图：
在这里插入图片描述
w12(1) 中的（1）表示第1层的权重，右下角前面的1表示后一层的第1个神经元，后面的2表示前一层的第2个神经元。
a1(1) 就代表后一层第1个的神经元。

2.2.2 各层间信号传递的实现

现在看一下从输入层到第1层的第1个神经元的信号传递过程，如下图所示：
在这里插入图片描述
注意那个涂黑的圆圈，它是偏置神经元“1”，由于它永远输入值为1的信号，所以给他涂黑了。它到a1的权重是b1，也就是偏置。现在用数学表达式表示a1：

换成矩阵的乘法运算，是如下所示：
在这里插入图片描述
下面我们用NumPy多维数组来实现式（3.9），把输入信号、权重、偏置设置成任意值。隐藏层的加权和用a表示，被激活函数转换后的信号用z表示。此外，图中h（）表示激活函数，我们使用的是sigmoid函数。

两个x，应该是两行，三个接收神经元，应该是三列。
实现：

Z1 = sigmoid(A1)
print(A1)
print(Z1)

如此一来，第0层到第1层的信号传递完成了。下面我们来看第1层到第2层的信号传递：
在这里插入图片描述
和上一层类似，只不过输入变成了3个。W的形状：三个输入，三行，两个接收，两列。（注意行是输入信号，列是接收神经元）偏置元素个数和接收神经元数量相等，应该有2个元素。z1、z2、z3。实现代码：

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

print(Z1.shape)
print(W2.shape)
print(B2.shape)

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

利用sigmoid函数对第2层神经元进行处理，如下图：
在这里插入图片描述
至此，第1层到第2层信号传递完毕。然后，实现第2层到第3层，实现方式照猫画虎。两个输入信号，W矩阵有两行，两个接收神经元，W矩阵有两列。偏置B有两个元素。

W3 = np.array([[0.1, 0.3],[0.2, 0.4]])
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)  # 或者 Y = A3

这里的输出层的激活函数不太一样，我们定义了identity_function( )函数（“恒等函数”），它会将输入按原样输出。这里的实现只是为了和之前的流程保持统一，输出层的激活函数用σ（）表示，不同于隐藏层的激活函数h（）。
在这里插入图片描述

2.3 输出层的设计

输出层所用的激活函数，要根据求解问题的性质决定。一般地，回归问题可以用恒等函数，二元分类问题可以用sigmoid函数，多元分类函数可以用softmax函数。
机器学习的问题大致可以分为分类问题和回归问题，分类问题是数据属于哪一个类别的问题，回归问题是根据某个输入预测一个（连续的）数值的问题。

2.3.1 恒等函数和softmax函数

        恒等函数会将输入按原样输出，对于输入信息，不加以任何改动直接输出。因此，恒等函数的转换处理可以用如下图示来表示：
在这里插入图片描述
        而softmax函数，分类问题中使用的softmax函数可以用下面的式子表示：

        exp(x)是表示 e^x 的指数函数。上式表示假设输出层共有n个神经元，计算第k个神经元的输出yk。softmax函数的分子是输入信号 ak 的指数函数，分母是所有输入信号的指数函数的和。
        用图表示softmax函数的话，如下图所示，图中，softmax函数的输出通过箭头与所有的输入信号相连，因为输出层的各个都受到所有输入信号的影响。
在这里插入图片描述
        下面我们用Python来实现softmax函数。

def softmax(a):
    exp_a = np.exp(a)               # 生成指数的输入信号 a
    sum_exp_a = np.sum(exp_a)       # 求出指数 a 的和（分母）
    y = exp_a / sum_exp_a           # softmax公式
    return y

2.3.2 实现 softmax 函数时的注意事项

虽然我们已经用Python写出了softmax函数，但是在计算机运算中，sotfmax函数存在缺陷，那就是溢出问题。softmax函数的实现中要进行指数函数的运算，此时指数函数的值容易变得非常大，e¹⁰ 、e¹⁰⁰的值已经很大，e¹⁰⁰⁰会返回一个表示无穷大的inf。这些超大值之间进行除法运算，会出现结果”不确定“的现象。因此，我们研究出了softmax函数的改进形式：
在这里插入图片描述
通过上面的推导，我们发现在进行softmax的指数运算时，加上或减去某个常数 C’ 不会改变运算的结果，为了防止溢出，我们的 C’ 一般使用输入信号中的最大值：

a = np.array([1010, 1000, 990])
y1 = np.exp(a) / np.sum(np.exp(a))
print(y1)       # 未被正确计算
c = np.max(a)   # 1010
y2 = np.exp(a - c) / np.sum(np.exp(a - c))
print(y2)       # 正确计算了

输出：

[nan nan nan]
[9.99954600e-01 4.53978686e-05 2.06106005e-09]

我们发现，通过减去输入信号中的最大值，原本为nan（not a number）的地方，现在被正确计算了，因此，我们可以改进刚刚softmax函数的实现方法。

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)           # 生成指数的输入信号 a （溢出对策）
    sum_exp_a = np.sum(exp_a)       # 求出指数 a 的和（分母）
    y = exp_a / sum_exp_a           # softmax公式
    return y

2.3.3 softmax 函数的特征

使用softmax函数，我们实际计算一下神经网络的输出：

a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
print(np.sum(y))

输出：

[0.01821127 0.24519181 0.73659691]
1.0

        可以发现，softmax函数的输出是 0.0 到 1.0 之间的实数。并且，softmax函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质，正因为如此，我们才可以把softmax函数的输出解释为“概率”。
        上面的例子可以解释成 y[0] 的概率是 0.018 (1.8%) ，y[1] 的概率是 0.245 ( 24.5 %) ， y[2] 的概率是 0.737（73.7%）。从概率的结果来看，可以说因为“第2个元素概率最高，所以答案是第2个类别“。而且还可以交代有74%的概率是第2个类别，25%的概率是第1个类别，1%的概率是第0个类别。这就是多元分类。
        要注意，即便用了softmax函数，各个元素之间的大小关系也不会改变，因为指数函数 y = exp（x）是单调递增函数，那么 a 的各元素大小关系和 y 的各元素大小关系也是一致的。a的最大值是第2个元素，那么y的最大值也是第2个元素。
        一般而言，神经网络只把输出值的最大神经元对应的类别作为识别结果，并且使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，输出层的softmax函数可以省略。在实际问题中，由于指数函数的运算需要一定的计算机运算量，所以输出层的softmax函数一般会被省略。
        机器学习问题求解步骤可以分为”学习“和”推理“两个阶段，推理阶段一般省略掉输出层的softmax函数，而在输出层使用它的理由是：神经网络的”学习“离不开它。

2.3.4 输出层的神经元数量

输出层的神经元数量要根据待解决的问题决定。对于分类问题，输出层神经元数量一般设为类别的数量。比如，对于某个输入图像，预测是图中的数字0到9中的哪一个的问题（10类别分类问题），可以设10个输出层神经元。
在这里插入图片描述
上图中，我们把输出的信号用灰度来表示信号强度，颜色越深，输出的值越大，因此y2预测类别正确的可能性很大，也就是说，这个输入的信号应该是“2”。

3.1 手写数字识别

了解了神经网络的结构，我们可以试着解决实际问题，比如：手写数字图像的分类。假设学习已经结束，我们利用学习到的参数，实现神经网络中的“推理处理”。这个推理处理也被称为神经网络的前向传播。在使用神经网络解决问题时，也需要首先使用训练数据（学习数据）进行权重参数的学习；进行推理时，使用刚才学习到的参数，对输入数据进行分类。

3.1.1 MNIST数据集

MNIST数据集是机器学习领域最有名的数据集之一，它由0到9的数字图像构成，训练图像有6万张，测试图像有1万张。一般使用MNIST数据集的方法是，先用训练图像学习，再用学到的模型度量能在多大程度上对测试图像进行正确的分类。
在这里插入图片描述
MNIST的图像数据是 28 pixels × 28 pixels 的灰度图像（1通道），各个像素的取值在0到255之间。我们利用Python导入MNIST数据集：

import sys, os
sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定
from dataset.mnist import load_mnist

# 第一次调用会花费几分钟 ……
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,
normalize=False)

# 输出各个数据的形状
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
print(x_test.shape) # (10000, 784)
print(t_test.shape) # (10000,)

导入mnist.py中的load_mnist函数，读入MNIST数据集，下面来介绍一下这个load_mnist函数。
        这个函数以“**（训练图像，训练标签），（测试图像，测试标签）”**的形式返回读入的MNIST数据。此外，还可以像load_mnist(normalize=True, flatten=True, one_hot_label=False)这样，设置3个参数。
        第一个参数normalize设置是否将输入图像正规化为0.0到1.0的值，若设为False，则输入图像像素会保持原来的0到255。
        第二个参数flatten设置是否展开输入图像（变成一维数组）。如果设为False，则输入图像为 1 × 28 × 28 的三维数组；若设置为True，则输入图像会保存为由784个元素（1 × 28 × 28 = 784）构成的一维数组。
        第三个参数one_hot_label设置是否将标签保存为 one-hot 表示（one-hot representation）。 one-hot 表示是仅正确解标签为1，其余皆为0的数组，就像 [ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0] 这样（这个意思是数字是“2”），若one_hot_label为False时，将正确解保存为数字本身；若为True，保存为one-hot（独热编码）表示。
        然后，我们试着显示MNIST图像，同时也确认一下数据。图像的显示使用PIL（Python Image Library）模块，执行下述代码后，可以显示出训练图像中的第一张。

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image


def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label)  # 5

print(img.shape)  # (784,)
img = img.reshape(28, 28)  # 把图像的形状变为原来的尺寸
print(img.shape)  # (28, 28)

img_show(img)

输出：
在这里插入图片描述

5
(784,)
(28, 28)

这里需要注意的是， flatten=True时读入的图像是以一列（一维）NumPy数组的形式保存的。因此，显示图像时，需要用reshape( )方法来重新改变图像的形状，更改NumPy数组的形状。（784，)是784行的一列，（28，28）是二维数组。此外，还需要把保存为NumPy数组的图像数据转换为PIL用的数据对象，这个转换处理由Image.fromarray（）来完成。

3.1.2 神经网络的推理处理

下面，我们对这个MNIST数据集实现神经网络的推理处理。神经网络输入层有784个神经元（图片的784像素），输出层有10个神经元（10种数字）。此外，这个神经网络有2个隐藏层，第1个隐藏层有50个神经元，第2个隐藏层有100个神经元。这个50和100可以设置为任何值。下面，我们先定义 get_date( )、init_network( )、predict( ) 这3个函数。

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

这里需要注意的是，init_network( ) 会读入保存在 pickle 文件 sample_weight.pkl 中学到的权重参数。Python有pickle这个便利的功能，它可以将程序运行中的对象保存为文件。如果加载保存过的pickle文件，可以立刻复原之前程序运行中的对象。sample_weight.pkl中以字典变量的形式保存了权重和偏置参数。get_data( ) 函数负责读取图像数据，predict( ) 函数负责进行神经网络的信号处理。
现在，我们用这3个函数来实现神经网络的推理处理。然后评价它的识别精度（accuracy），即能在多大程度上正确分类。

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y) # 获取概率最高的元素的索引
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

        首先获得MNIST数据集，生成网络。接着，用for语句逐一取出保存在x中的图像数据，用 predict( ) 函数进行分类。获取概率最高的元素索引赋值给 p 。predict ( ) 函数以NumPy数组形式输出各个标签对应的概率。比如输出 [ 0.1, 0.3, 0.2, … , 0.04] ，就表示这个数字是“0”的概率是0.1，是“1”的概率是0.3…然后我们取出这组概率中的最大值的索引（用np.argmax( )函数），作为预测结果。最后，用这个得到的索引值与神经网络中预测的答案和正确解标签（也就是t [ i ]，t 里存储的是每个图像的正确解，比如，这个 x [ i ] 数字是“7”，那么 t [ i ] 就等于 7 ）作比较，若相等，则说明这个数字被正确分类了，让统计量 accuracy_cnt 加 1，最后用这个统计量除以总的图像数，就是正确分类率了。
        执行上面的代码后，会显示“Accuracy:0.9352”。表示有93.52%的数据被正确分类了。
        另外，在这个例子中，我们把load_mnist函数的参数normalize甚至成了True，设置为True后，函数内部会进行转换，把图像的各个像素值除以255，使得数据的值在 0.0 ~ 1.0 的范围内。像这样，把数据限定到某个范围内的处理称为正规化（normalization）。此外，对神经网络的输入数据进行某种既定的转换称为预处理（pre-processing）。实际上，很多预处理都会考虑到数据的整体分布，比如，利用数据整体的均值或标准差，移动数据，让数据整体以0为中心分布；或者进行正规化，把数据的延展控制在一定范围内；此外，还有将数据整体的分布形状均匀化的方法，即数据白化（whitening）等。

3.1.3 批处理

刚才，我们使用Python实现了神经网络处理MNIST数据集的过程。现在，我们来关注输入数据和权重参数的“形状”。
使用Python输出刚才的神经网络各层的权重的形状。

x, _ = get_data()
network = init_network()
W1, W2, W3 = network['W1'], network['W2'], network['W3']
print(x.shape)
print(x[0].shape)
print(W1.shape)
print(W2.shape)
print(W3.shape)

输出：

(10000, 784)
(784,)
(784, 50)
(50, 100)
(100, 10)

我们通过上述结果确认一下，多维数组的对应维度的元素个数是否一致（省略了偏置），根据输出，用图表示如下所示。可以发现，多维数组的对应维度的元素个数确实是一致的。此外，我们还可以确认，最终的结果是输出了元素个数为10的一维数组。
在这里插入图片描述

        从上图我们可以看出来，X是指在处理流程中的一张输入图片（比如代码里写的x[0]，就是指第一张图片），然后它的形状是784个元素组成的一维数组（是由 28 × 28 的二维数组flatten以后转换成的）。如果我们想同时处理多张图片，比如一口气处理100张呢？这个时候，我们可以把X的形状改成100 × 784，将100张图片打包作为输入数据，那么图就应该变成这样：
在这里插入图片描述
        此时Y就成了 100 × 10 的二维数组，每一行是一张图片的正确解的一维数组。比如，x[0] 和 y[0] 中保存了第0张图像及其推理结果，x[1] 和 y[1] 保存第1张，等等。
        这种打包式的输入数据称为批（batch）。
        下面我们进行基于批处理的代码实现。

x, t = get_data()
network = init_network()

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

        让我们解析一下。首先range( )函数，指定range(start, end)，则会生成一个由 start 到 end - 1 之间的整数构成的列表。像 range(start, end, step) 这样指定3个整数，则生成的列表会以step为步长。因此，我们把步长设为batch_size，然后用 x[ i : i + batch_size ] 取出每一批次的元素，也就是 x[0:100] 、x[100:200]…
        然后，y_batch 对应 x_batch ，得到每一批数据的结果。
        然后，通过argmax( ) 获取值最大的元素的索引。不过需要注意的是，我们指定了参数 axis = 1。这指定了在 100 × 10 的数组中，沿着第1维方向（以第1维为轴，这里的第1维是行方向，而第0维是列方向）找到最大的元素的索引。这里看一个例子：

>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6],
...		[0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])   # 4行3列
>>> y = np.argmax(x, axis=1)
>>> print(y)
[1 2 1 0]

        这个就是按照第1维，也就是行方向，找最大值元素所在下标。
        那么，这里的argmax（y_batch, axis = 1)其实是在找出每一行（也就是每一张图片）被识别出的结果（因为是几的话，它在的那一列就是1，其他列都是0，找出最大值下标，这个下标值也就是这个数字本身了），比如：[ 0, 0, 1, 0, 0, 0, 0, 0 ,0 ,0 ]，说明这个数字是2，此时argmax（）它得到的结果刚好是“2”。
        最后，我们把以批为单位进行分类的结果赋值给p，和验证集t [ i : i + batch_size ]作比较。为此，需要在NumPy数组间使用比较运算符（==）生成由True/False构成的布尔型数组，并计算True的个数，这就是，被正确分类的数字个数了。可以用下面的例子帮助理解：

>>> y = np.array([1, 2, 1, 0])
>>> t = np.array([1, 2, 0, 0])
>>> print(y==t)
[True True False True]
>>> np.sum(y==t)
3

本次，我们介绍了神经网络的前向传播，神经网络和感知机在按层传递信号这一点上是相同的，但是，他们的激活函数不同，神经网络使用sigmoid，而感知机使用阶跃函数。sigmoid函数对神经网络的学习很重要，我们下次再介绍。