数据结构的基本概念及队列与栈的基本实现

一数据结构的基本概念

1 hash表

①dict底层结构使用的哈希表

◆为了支持快速查找使用了哈希表作为底层结构，哈希表的实现原理，底层其实就是一个数组

◆哈希表平均查找时间复杂度O(1)

◆CPython解释器使用二次探查解决哈希冲突问题

②list与tuple的区别

◆都是线性结构，支持下标访问

◆list是可变对象， tuple不可变（不准确，应该是保存的引用不可变，即你没法替换掉这个对象 ），如([1],2,3)[0].append(4)则会变成([1,4],2,3)

◆list没法作为字典的key， tuple可以(可变对象不可hash)

③Python dict/set底层都是哈希表

◆哈希表的实现原理，底层其实就是一个数组

◆根据哈希函数快速定位一个元素，平均查找O(1)，非常快

◆不断加入元素会引起哈希表重新开辟空间，拷贝之前元素到新数组

哈希冲突如何解决：链接法、开放寻址法（即探查法，包括线性探查、二次探查）

 

2.二叉树[涉及到递归和指针操作，常结合递归考察。常考题：二叉树的镜像（对左右子树进行递归）；如何岑旭便利二叉树（广度优先）]

二叉排序树，又称为二叉查找树或者二叉搜索树。

性质：可以是空树，也可以是具有下列性质的二叉树。

1)若左子树不空，则左子树上的所有节点的值均小于它的根节点的值；

2)若右子树不空，则右子树上的所有节点的值均大于或等于它的根节点的值；

3)左右子树也分别为二叉排序树。

一链表

 

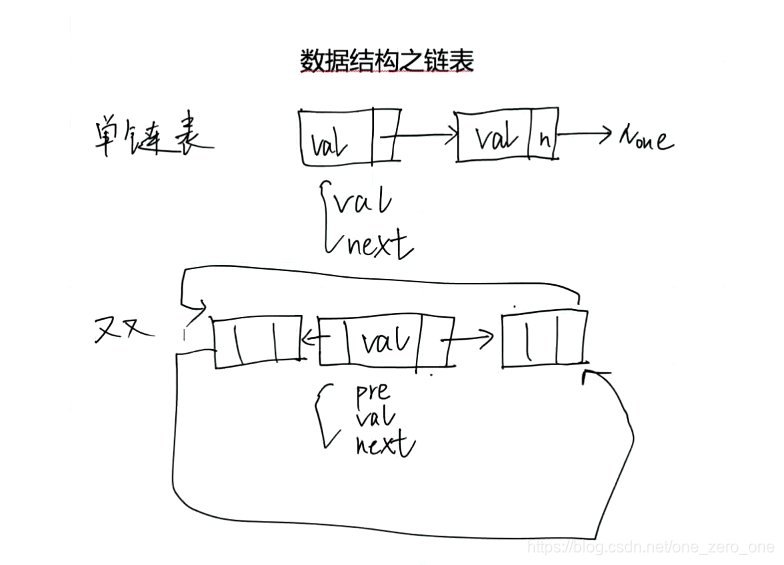
二  栈：后进先出

class Stack(object):
    def __init__(self):
        self.__list=[]

     #添加一个新元素到栈顶
    def push(self,item):
        self.__list.append(item)

    #弹出栈顶元素
    def pop(self):
        return self.__list.pop()


    # 返回栈顶元素
    def peek(self):
        if self.__list:
            return self.__list[-1]
        else:
            return None

    def is_empty(self):
        return self.__list==[]

    def size(self):
        return len(self.__list)
if __name__=='__main__':

    s=Stack()
    s.push(1)
    s.push(2)
    s.push(3)
    print(s.pop())

三 队列:先进先出

class Queue(object):
    def __init__(self):
        self.__list=[]

    # 往队列添加元素 两者方式的时间复杂度不一，
    def enqueue(self,item):
        self.__list.append(item)   #尾部append添加o(1)
        # self.__list.insert(0,item)   #o(n)

    # 从队列头部删除元素
    def dequeue(self):
        return self.__list.pop(0)  #先进先出  o(n)
        # self.__list.pop()      #o(1)

    def is_empty(self):
        return self.__list==[]

    def size(self):
        return len(self.__list)

if __name__=="__main__":
    q=Queue()
    q.enqueue(1)
    q.enqueue(3)
    q.enqueue(5)
    print(q.dequeue())
    print(q.dequeue())
    print(q.dequeue())

class Double_Queue(object):
    def __init__(self):
        self.__list=[]

    # 往队列头部添加元素 两者方式的时间复杂度不一，
    def add_front(self,item):
        self.__list.insert(0,item)   #o(n)

    # 往队列尾部添加元素
    def add_rear(self,item):
        self.__list.append(item)   #尾部append添加o(1)

    # 从队列头部删除元素
    def pop_front(self):
        return self.__list.pop(0)  #先进先出  o(n)
        # self.__list.pop()      #o(1)

    # 从队列尾部删除元素
    def pop_rear(self):
        return self.__list.pop()
        # self.__list.pop()      #o(1)

    def is_empty(self):
        return self.__list==[]

    def size(self):
        return len(self.__list)