矩阵使用过程中问题记录

仅用于记录本人四元数学习与使用过程中，概念不清晰，以及踩得坑的情况

参考网址：
四元数公式计算集合：
https://zhuanlan.zhihu.com/p/442146306
矩阵旋转与左乘右乘
https://blog.youkuaiyun.com/weixin_45632220/article/details/117735223
左乘固定坐标系，右乘相对坐标系原理
https://www.zhihu.com/question/407150749

四元数，顾名思义是秩为4的超复数。
z = a + bi， i^2 = -1。

理论1：
基于全局坐标系的旋转变换左乘旋转矩阵，基于自身坐标系的旋转变换右乘旋转矩阵
左乘是相对固定坐标系，右乘是相对当前坐标系
p3 = Mz(γ) x My(β) x Mx(α) x p0 左乘
p0 = Mx(α) x My(β) x Mz(γ) x pC 右乘

复数部分

两个实部相等，虚部互为相反数的复数互为共轭复数

定义复数q:q=cosθ + isinθ。
让任意复数进行任意角度的旋转变换：
p = a + bi;
q=cosθ + isinθ;
pq = (a + bi)(cosθ + isinθ)
a’ + b’i = acosθ - bsinθ + (asinθ + bcosθ)i
转换为矩阵就是
$$\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$
回顾下旋转矩阵的推导结果：
$$\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$
上述矩阵是以单位向量（0，1）和（1，0）两坐标轴组成的坐标系旋转θ的操作。
复数映射矩阵为以（1， 0i），（0， 1j）两坐标轴形成的坐标系旋转θ的操作。

四元数

形式：q = s + xi + yj + zk
其中i^2 = j^2 = k^2 = ijk = -1;

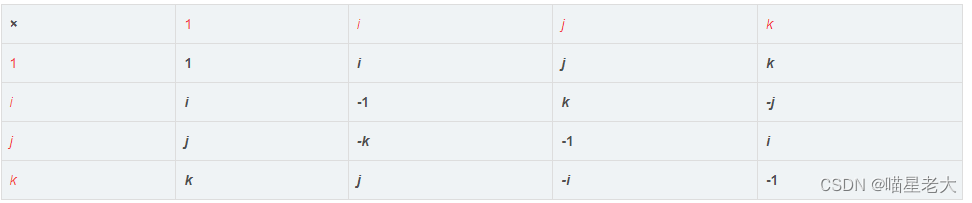
同时符合叉乘规则

四元数乘法运算：

矩阵的左右乘

左乘旋转矩阵绕固定坐标系旋转，右乘旋转矩阵绕自身坐标系旋转
这里的左右乘指的并不是某一向量左乘或者右乘旋转矩阵，而是多个旋转矩阵的组合方式是左乘还是右乘。
绕固定坐标系旋转讨论的是向量的旋转，绕自身坐标系旋转讨论的是坐标变换
1.旋转矩阵左乘
我想要一个向量p0先绕x轴转α度，再绕y轴转β度，最后绕z轴转γ度，求旋转后向量的位置。
可见这是一个旋转矩阵组合的问题，之前讨论过，向量绕某一坐标轴旋转在数学上展现为向量左乘旋转矩阵，我们按照题意，当然是先让它绕x轴旋转：
p1 = Mx(α) x p0;
再绕y：
p2 = My(β) x p1;
再绕z；
p3 = Mz(γ) x p2;

连起来就是
p3 = Mz(γ) x My(β) x Mx(α) x p0
旋转矩阵：
R = Mz(γ) x My(β) x Mx(α);

2.旋转矩阵右乘
右乘讨论的就是坐标变换了，来看问题：已知在C坐标系下表示的向量pC，我想求pC在原始坐标系0下的表示p0，已知C坐标系由原始坐标系0绕轴X0旋转α度成为坐标系A，再绕轴YA旋转成为坐标系B，再绕轴ZB旋转成为坐标系C。
p点在B坐标系下的坐标，乘以旋转矩阵，得到的是在A坐标系下的坐标，而B坐标系是由A坐标系转了α角转过去的，可以发现，这是一种“退回”效果，也就是p点在旋转后的坐标系下的坐标左乘旋转矩阵后，会变为旋转前坐标系下的坐标，这种效果表明旋转后的坐标系一定是绕旋转前坐标系的某一轴转过去的，对于旋转前的坐标系，可以理解为绕自身坐标系的坐标轴旋转后成了旋转后的坐标系。换句话说，因为你退回来得到的是前坐标系下的坐标，你转过去也必须是绕前坐标系中的坐标轴转过去的，故我们称之为绕自身坐标系旋转。
从C退到B:
pB = Mz(γ) x pC;
从B推导A：
pA = My(β) x pB;
退回最初；
p0 = Mx(α) x pA;

连起来就是
p0 = Mx(α) x My(β) x Mz(γ) x pC
旋转矩阵：
R = Mx(α) x My(β) x Mz(γ)
之前说过坐标系C是由坐标系0经过绕轴X0变为坐标系A，再绕轴YA变为坐标系B，再绕轴ZB旋转才得到的，为了使其退回去，看看旋转矩阵R的写法，是不是绕x轴旋转矩阵右乘y轴旋转旋转右乘z轴旋转矩阵？这就是我们所说的绕自身坐标轴旋转要右乘旋转矩阵。

参考一位大佬说的话：
1、如果两个变换的叠加：M₂M₁表示先进行M₁变化，再进行M₂变换，这里M₁，M₂都是自然基坐标系下。
2、如果M₂变换是在M₁坐标系基础上进行的，那么根据相似矩阵把M₂转换成自然基坐标系，M₁M₂M₁${}^{-1}$
3、那么两个变换叠加就是（M₁M₂M₁${}^{-1}$）M₁ = M₁M₂
这样，如果每个变换都是在上个变换基础上进行的，那么只要把矩阵顺序反过来就行了。
所有变换都在自然基下：M₁M₂M₃M₄
每个变换都在前一个变换后的坐标系下：M₄M₃M₂M₁

旋转矩阵的两种含义

旋转矩阵其实有两种含义，旋转向量和坐标变换。这两者的旋转矩阵是一样的。
坐标变换和旋转向量虽然都是对应同一个旋转矩阵，但其理解的含义还是有很大差别的，尤其是有多次旋转操作时。

坐标变换：

指一个向量在不同坐标系下有不同的坐标表示。
如果发生了多次旋转，那么应该以旋转后的最终状态为起点，从最近一次旋转开始，依次左乘一个旋转变换矩阵；那如果以旋转前的初始状态为起点，从最早的一次旋转开始，依次右乘对应的旋转变换矩阵。这样才能“抵消”旋转产生的影响，求出向量在旋转前坐标系中的坐标表示。

旋转向量：

指坐标系不动的情况下旋转向量。
如果向量发生多次旋转，应该是按照旋转顺序依次左乘对应的旋转矩阵。