又见斐波那契(构造矩阵，矩阵快速幂)

最新推荐文章于 2025-06-01 00:01:08 发布

原创最新推荐文章于 2025-06-01 00:01:08 发布 · 1k 阅读

0 ·

CC 4.0 BY-SA版权

矩阵快速幂专栏收录该内容

2 篇文章

订阅专栏

本文介绍了一种使用矩阵快速幂的方法来高效计算一个变种斐波那契数列的问题。该方法适用于处理大规模数据输入，并且通过模运算解决了数值过大的问题。文章提供了完整的C++代码实现，可用于解决类似数列计算问题。

链接：https://www.nowcoder.com/acm/contest/105/G
来源：牛客网

题目描述

这是一个加强版的斐波那契数列。

给定递推式

求F(n)的值，由于这个值可能太大，请对10 ⁹+7取模。

输入描述:

第一行是一个整数T(1 ≤ T ≤ 1000)，表示样例的个数。
以后每个样例一行，是一个整数n(1 ≤ n ≤ 10¹⁸)。

输出描述:

每个样例输出一行，一个整数，表示F(n) mod 1000000007。

思路：构造矩阵，矩阵快速幂；

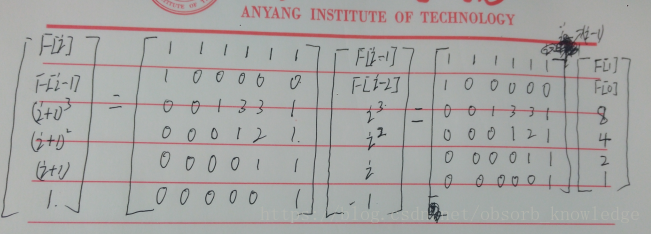
代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;

#define ll long long 
const ll mod = 1000000007;

struct node
{
	ll a[6][6];
};

node s_cheng(node tt,node kk)
{
	int i,j,k;
	node res;
	memset(res.a,0,sizeof(res.a));
	for(i=0;i<6;i++)
		for(j = 0;j<6;j++)
			for(k = 0;k<6;k++)
			res.a[i][j] = (res.a[i][j]+ tt.a[i][k]*kk.a[k][j])%mod;
	return res;
}

node p_pow(node tt,ll n)
{
	node res;
	memset(res.a,0,sizeof(res.a));
	res.a[0][0] = res.a[1][1] = res.a[2][2] = res.a[3][3] = res.a[4][4] = res.a[5][5] = 1;
	while(n)
	{
		if(n&1) res = s_cheng(res,tt);
		n>>=1;
		tt = s_cheng(tt,tt);
	}
	return res;
}

int main()
{
	ll n;
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%lld",&n);
		node res,tt;
		memset(res.a,0,sizeof(res.a));
		memset(tt.a,0,sizeof(tt.a));
		if(n<=1)
		{
			printf("%lld\n",n);
			continue;
		}
		
		res.a[0][0] = 1;
		res.a[2][0] = 8;
		res.a[3][0] = 4;
		res.a[4][0] = 2;
		res.a[5][0] = 1;
		res.a[1][0] = 0;
		tt.a[0][0] = tt.a[0][1] = tt.a[0][2] = tt.a[0][3] = tt.a[0][4] = tt.a[0][5] = 1;
		tt.a[1][0] = 1;
		tt.a[2][2] = tt.a[3][3] =tt.a[4][4] =tt.a[5][5]  = 1;
		tt.a[2][5] = tt.a[3][5] =tt.a[4][5]= 1;
		tt.a[2][3] = tt.a[2][4] = 3;
		tt.a[3][4] = 2;
		tt = p_pow(tt,n-1);
		res = s_cheng(tt,res);
		printf("%lld\n",res.a[0][0]);
	}	
	return 0;
}