具时滞的双积分过程控制
摘要
在许多过程工业中,储罐用于储存需要液位控制的液体。每个储罐中的液体高度表现出积分加时滞(IPDT)特性。当两个此类储罐串联连接时,形成双积分加时滞(DIPDT)过程。DIPDT过程本身对阶跃输入/变化具有不稳定性。因此,建议使用控制器来稳定液位的闭环响应。在反馈回路中增加一个附加环节,以消除DIPDT过程的不稳定性。通过继电器测试获取系统的极限特性,用于设计PID控制器。同时,辨识过程参数,并采用洛朗级数逼近方法合成内模控制(IMC)‐PID整定规则,用于PID控制器。计算并比较闭环性能。同时求取控制器的IAE和灵敏度。
索引术语 – DIPDT系统, 继电器反馈, PID控制器, 灵敏度。
I. 引言
所提出的系统为具时滞的双积分过程。储罐的传递函数为 $1/(τ_ps + 1)$。当两个储罐串联连接时,其传递函数变为 $1/(τ_ps + 1)^2$。工业中使用的储罐具有大容量,即大的 $τ_p$。因此,我们可以将 $1/(τ_ps + 1)^2$ 近似为 $K_p/s^2$。
化工过程工业中使用的许多装置,如加热锅炉、间歇式化学反应器、液体储罐或液位系统等,都属于积分过程,其动态响应非常缓慢,并具有大的主导时间常数。由于循环回路和组分分析回路等中的传输延迟,在过程工业所用的大多数过程中存在时间延迟。因此,两个串联储罐的组合传递函数为 $K_p e^{-Ds}/s^2$,其中 $D$ 为时滞常数,该过程可称为双积分加时滞过程(DIPDT)。DIPDT过程也在许多其他系统中出现。此前已有针对多种积分过程的控制器设计尝试[7,8,17]。对DIPDT过程进行控制器参数设计具有挑战性。
此处已进行研究。已有研究表明,PID控制器是主要工业中实施的紧凑型控制器,当前的研究重点在于采用先进控制器的概念来综合PID参数[1, 2, 3, 5]。在此情况下,IMC‐PID因其在设定值跟踪和鲁棒性之间的最佳权衡而被优先考虑[13, 19]。本文将IMC‐PID的定性性能与通过继电器反馈方法整定的常规PID进行比较[1, 4]。本文结构如下:第二节介绍继电器反馈方法,第三节讨论利用洛朗级数进行控制器参数设计并附有示例,第四节比较控制器性能,第五节描绘过程的灵敏度,第六节总结所提出的工作。
II. 继电器反馈
DIPDT系统是一种带死区时间的双重积分过程。其名称本身就意味着传递函数分母中含有 $s^2$ 项,分子中含有 $e^{-Ds}$ 项。$s^2$ 项的时域形式为 $t$。DIPDT系统本身无法产生持续振荡。因此,需要在过程的反馈回路中加入一个能够消除 $t$ 的变化率并给出期望输出的传递函数。经发现,增益为1的 $du/dt$ 满足该约束条件。在过程中使用继电器来识别其参数[18, 20]。采用继电器反馈测试产生持续振荡,作为传统连续循环技术的替代方法,因为它在确定临界增益和临界频率方面非常有效。在继电器反馈方法中,继电器与过程模型相连。对于时滞过程,继电器响应比输入滞后时间为 $D_p$,可通过将输出平移时间 $D_p$ 实现输出同步。
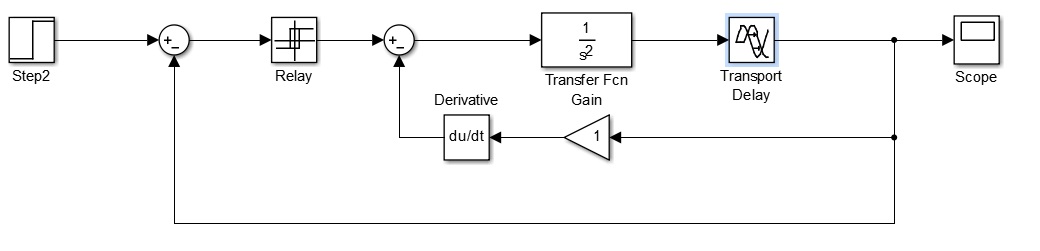
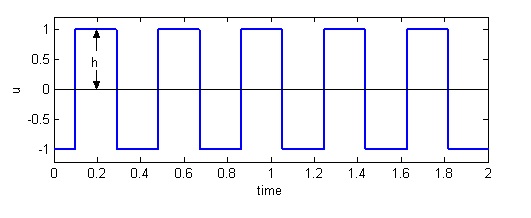
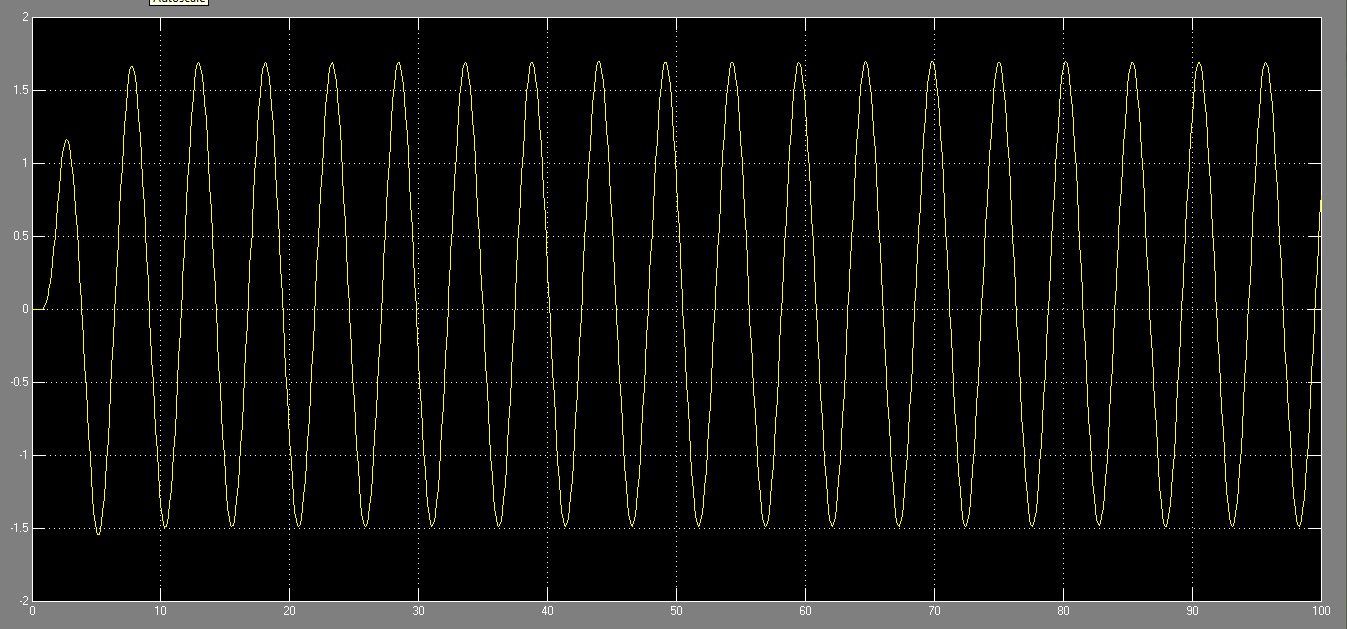
从上图可以看出存在持续振荡,由此确定临界增益 $K_u = 4h/πa$ 和临界周期 $P_u$(振荡周期)分别为0.7490和20秒。根据临界周期和临界增益可确定PID控制器参数。
A. 解析表达式的推导
[9]解析表达式通常用于估计过程参数,并用于设计控制器的自整定。继电器反馈测试中观察到的临界增益和周期已被用于获得n阶系统的通用表达式。DIPDT系统在单位阶跃输入下的闭环传递函数可写为
$$
Y(s) = \frac{1}{s^2 + k_p e^{-Ds}}
\tag{1}
$$
上述方程可写为
$$
s^2 Y(s) + k_p e^{-Ds} Y(s) = 1
\tag{2}
$$
$$
k_p e^{-Ds} Y(s) = 1 - s^2 Y(s)
\tag{3}
$$
在初始阶段,响应为零时,$y(t)$ 使用 $t = t_1$ 计算,对该部分取公式(1)的拉普拉斯变换后得到的响应为 $Y_1(t)$,并写入方程(4)
$$
Y_1(t) = \frac{k t^2}{2} - k_p Y_1(t)
\tag{4}
$$
令 $k’ = \frac{k}{2 + k_p τ}$,则
$$
Y_1(t) = k’ t^2
\tag{5}
$$
时间延迟被引入到下一段曲线中,即 $Y_2(t) = y(t - D) - Y_1(t - D)$,其中将 $t$ 替换为 $t - D$;以及
$$
Y_3(t) = y(t - D - P_u/2) - Y_2(t - D - P_u/2) + Y_2(t - D)
$$
其中将 $t$ 替换为 $t - D - P_u/2$,因此
$$
Y_2(t) = k’(t - D)^2 \equiv Y_2(t) = k’(t^2 - 2tD + D^2)
$$
类似地
$$
Y_3(t) = k’\left(t - D - \frac{P_u}{2}\right)^2
$$
类似地,通过将 $t$ 替换为 $t - D - (n-1)\frac{P_u}{2}$,可计算出曲线的第 $n$ 段响应
$$
Y_n(t) = y(t - D) - \sum_{i=1}^{n-1} (-1)^{i} Y_i\left(t - D - (i-1)\frac{P_u}{2}\right)
$$
当 $n$ 趋近于 $∞$,
$$
(-1)^{n-1} y\left(t - D - (n-1)\frac{P_u}{2}\right)
$$
变为零,然后
$$
Y(t) = \sum_{n=1}^{\infty} (-1)^{n+1} k’ \left[t - D - (n-1)\frac{P_u}{2}\right]^2
$$
让我们假设
$$
f_1 = D^2 - \frac{(P_u)^2}{4},\quad f_2 = -\frac{(P_u)^2}{4},\quad f_3 = \frac{(P_u)^2}{4}
$$
$f_1$ 收敛到0,
$f_2$ 收敛到 $(-1)^n/2$,
$f_3$ 收敛到 $(-1)^{n}(n(n-1))/2$,因此
$$
Y(t) = \frac{k’}{2} \left[ (t - D)^2 + \frac{P_u}{2}(t - D) + \cdots \right]
$$
The expression so obtained is divergent in nature. It is difficult to obtain a convergent series in time domain using $D_s τ$, so we proceed to be tuning in s domain.
III. PID参数整定
许多作者通过近似现有控制器的方法对PID参数进行了整定[12, 13, 14]。本文采用基于洛朗级数近似的IMC‐PID参数整定规则[10,11],因为洛朗级数在零附近展开时,前三个项起主导作用,能够解决泰勒级数或麦克劳林级数无法处理的奇异性问题。将模型与PID控制器结合,可获得控制器的定性性能。
$$
G_c(s) = \frac{φ(s)}{β(s)} = \frac{f(s)}{1 + s}
$$
比较上述两个方程的 $s$ 项系数,可得
$$
k_c = f’(0)/φ(0)
\tag{6}
$$
$$
\tau_I = f(0)/φ(0)
\tag{7}
$$
$$
\tau_D = \frac{f’‘(0)/2 + f’(0)β’(0)}{φ(0)}
\tag{8}
$$
参考Panda 2003,[10,11],DIPDT系统的控制器参数已被确定。
DIPDT系统的控制器参数为
这里给出一阶加纯滞后系统以便清楚理解。一阶加纯滞后传递函数为
$$
G_p(s) = \frac{K_p e^{-D_p s}}{τ_p s + 1}
$$
其中 $D_p$—死区时间,$G_p$ —过程,$K_p$ —过程增益,$τ_p$——时间常数。此处通过展开的洛朗级数将期望闭环响应的内模控制器近似为理想PID控制器的形式,而其他研究在此PID结构近似方面也有相应贡献[6, 16, 17]。
$$
\frac{1}{G_c(s)} = \frac{(τ_p s + 1)(1 + s)}{K_p e^{-Ds}} - 1
$$
substitute
$$
e^{-Ds} = 1 - Ds + \frac{(Ds)^2}{2!} - \frac{(Ds)^3}{3!} + \cdots
$$
we get
参数如下
$$
k_c = \frac{K_p (τ_p + D)}{λ}
$$
$$
\tau_I = \frac{τ_p^2 + D τ_p + D^2/2}{λ}
$$
$$
\tau_D = \frac{τ_p D + D^2/2}{λ}
$$
现在将上述方法应用于DIPDT系统以获得控制器参数。
DIPDT传递函数为
$$
G_p(s) = \frac{K_p e^{-Ds}}{s^2}
$$
Here,
$$
f(s) = \frac{1}{k_p s^2 (1 - e^{-λs})}
$$
上述 $f(s)$ 在应用洛朗级数时,使控制器的值为零。
So we assume
$$
f(s) = \frac{1 + λs}{k_p s^2 (1 - e^{-λs})}
$$
and results obtained 如下所示:
$$
f(0) = 0.05,\quad f’(0) = 0.4549,\quad f’‘(0) = 0.763
$$
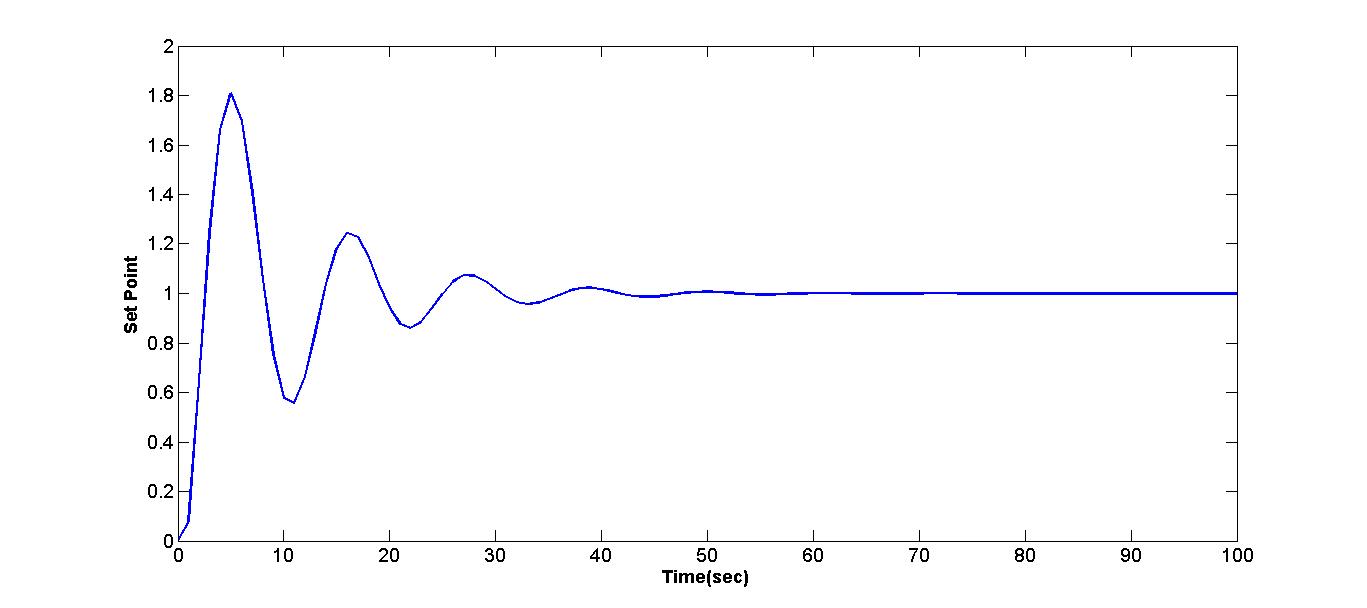
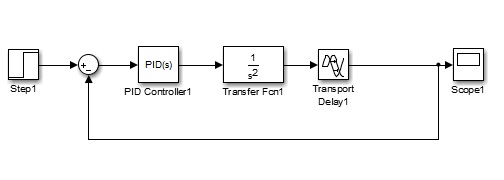
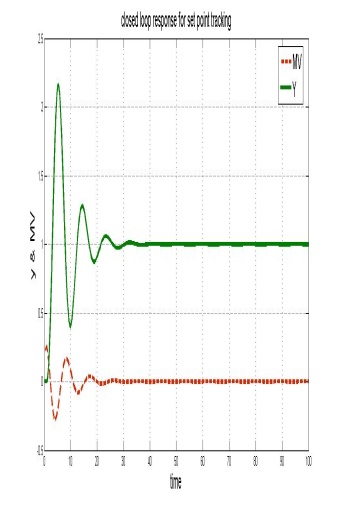
通过将上述值代入公式 [6, 7, 8] 可得到 PID 参数。在下述模型(图5)中为控制器设置这些值,可得到如图6所示的响应。
IV. IAE – 积分绝对误差
$$
\text{IAE} = \int |Y_{sp} - Y| \, dt
$$
IAE 是误差值的绝对值。
此处计算的 IAE 取决于 $ K_p $,因此通过将计算得到的 $ Y $ 除以 $ K_p $ 对误差进行归一化。归一化后的误差为 0–3%。
V. 灵敏度
控制器灵敏度通过绘制不同 $ K_p $ 和 $ D $ 值下 $ S $ 与 $ \omega $ 的关系来测量。
对数 $ S $ 与对数 $ \omega $ 进行绘图。
$$
S(s) = \frac{1}{1 + k_p e^{-Ds} / s^2}
$$
针对 $ K_p $ 值在 0.7 到 2 之间、$ D $ 值在 0.8 到 0.9 之间的范围绘制了图形。所有这些图形从不同的起点开始,但最终都稳定在同一数值,即终值相同。当 $ K_p $ 和 $ D $ 的取值超出此范围时,图形不再表现出上述特性。因此,该 PID 控制器对 $ K_p $ 的灵敏度为 0.7,$ D $ 取值为 0.8,$ K = 1 $,$ \tau_D = 1 $,对应的灵敏度图如图7所示。
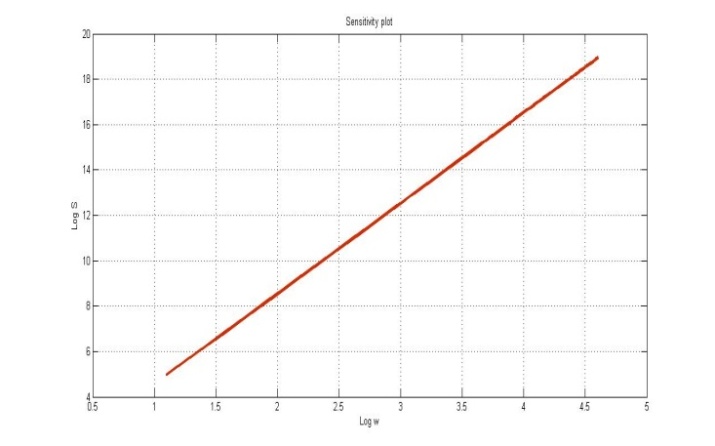
结果: 李等人参数与所提出参数的比较。
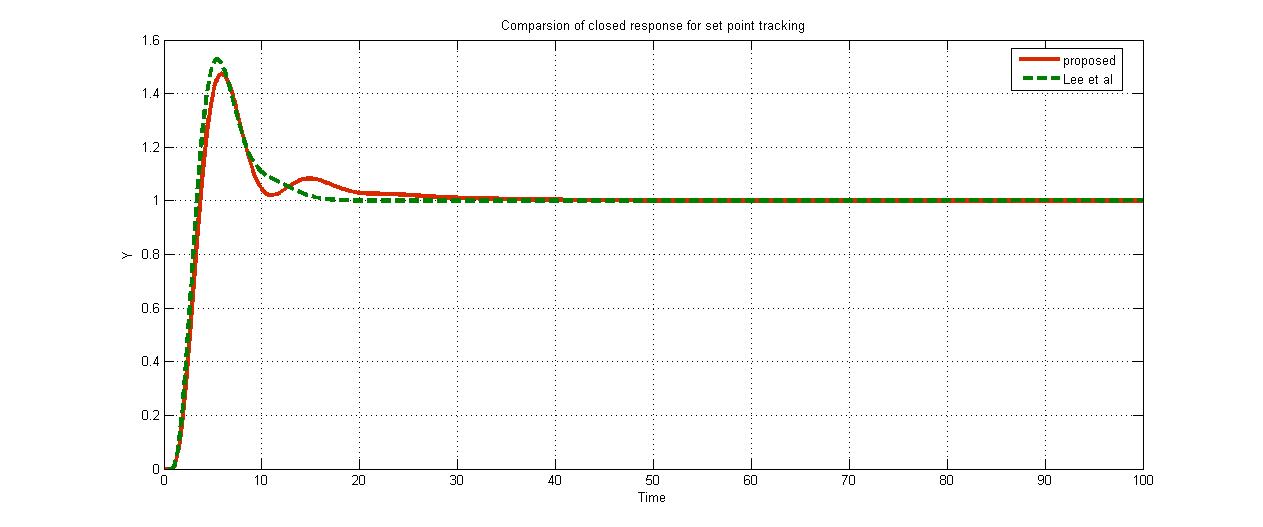
建议:
- 对 DIPDT 过程在稳定性方面的深入研究。
- 闭环传递函数可以通过(在反馈回路中用适当元素替换 $ du/dt $)重新表述,使其阶跃响应的时间序列成为收敛级数,从而得到合适的时间序列模型,可用于合成 IMC 规则。
- 可以设计并实现其他传统与启发式控制策略,并将其性能与当前策略进行比较。





















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








