数据结构与算法 二分查找

 

1. 二分查找原理：

条件：sorted :有序，单调递增，或者单调递减。

       Bounded:存在上下边界。

       Acssisible  by   index: 可到达。

时间复杂度：  log2(n)   空间复杂度  ：O（1）

图解：

 

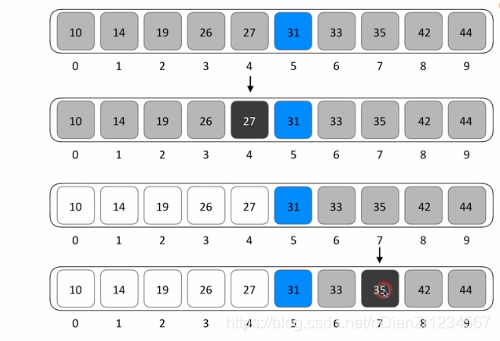
1.  小于中间数 左边查找，大于中间数右边查找。

      left =0 ,right=len(arry)-1;指向数组两端

代码

 

 

 

---

    while(left<=right){

   mid=(left+right)/2;

   if(arry[mid]==target){

   //find   taget !!!

    return mid;

}else  if（ arry[mid]>target）{

right= mid-1;// 左边查找

}else{

left= mid+1;//右边查找

}

return  -1;

 

}

#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
    int binarySearch(vector<int> nums, int val)
    {
        int low = 0, high = nums.size() - 1, mid;
        while (low < =high)
        {
            mid = (low + high) / 2;
            if (nums[mid] == val)
            {
                return mid;
            }
            else if (nums[mid] > val)
            {
                high = mid - 1;
            }
            else
                low = mid + 1;
        }
        return -1;
    }
};

 

复杂度

 

时间复杂度为O(log₂n),空间复杂度为O(1)
 

二分查找的应用：

 

leetcode-二分搜索：求一个数的平方根

2015年07月13日 11:35:08 zc02051126 阅读数：1931

解题思路：

• 设double low=0,double up=x
• double mid = (low + up) / 2
• 如果mid * mid > x,则up = mid;如果mid * mid < x,则low = mid;如果fabs(mid * mid - x) <= 1e-6,则返回mid,否则继续迭代计算

程序如下

#include<iostream>
#include<math.h>
#include<stdlib.h>
#include<stdio.h>

using namespace std;

double sqrt(double x)
{
    double low = 0;
    double up = x;
    double mid = (low + up) / 2;
    while(fabs(low - up) >= 1e-6)
    {
        if(mid * mid > x)
            up = mid;
        else if(mid * mid < x)
            low = mid;
        else if(fabs(mid * mid - x) < 1e-6)
            return mid;
        mid = (up + low) / 2;
    }
    return mid;
}



int main(int arvc, char** argv)
{
    double in = atof(argv[1]);
    double r = sqrt(in);
    printf("r = %f\n", r);
    return 0;
}