用于低功率应用的压电风能发电机的设计、建模与实验分析
摘要
在过去的几十年里,化石燃料和其他不可再生能源的消耗引发了人们对环境保护的担忧。鉴于此,本文提出了一种基于能量收集概念的风力涡轮机设计,并对其进行了表征以及数值与实验分析,用于为低功率(毫瓦)设备供电的压电换能器系统。该原型的尺寸约为 84.5 × 87 × 20 mm³;激励由永磁体实现,磁铁通过 120° lag 被粘接到发电机轴上。每个磁铁与一根钢梁(60 × 13 × 0.15 mm³)的自由端相互作用,钢梁表面附有压电陶瓷(PZT C‐64)。通过多种数值与实验分析,优化了梁的几何形状、压电尺寸、固定在梁末端的质量、产生的电压,特别是最大输出功率。最后,报告了在不同工作条件下性能最佳的模型,单根梁的最大输出功率为 2.06 毫瓦,三根梁并联时的最大输出功率为 3.78 毫瓦,相应的功率密度分别为 18.8 μW/mm³ 和 11.5 μW/mm³。
关键词 :压电发电机,风力发电机,低功率,压电能量收集
1. 引言
近年来,已发表多项关于利用压电材料从环境中提取能量的技术和装置的研究[1, 2, 3, 4, 5]。尽管振动动能应用最为广泛,但也可从其他多种来源获取能量[6],包括电磁装置,其在能量转换方面也具有巨大潜力[7, 8]。
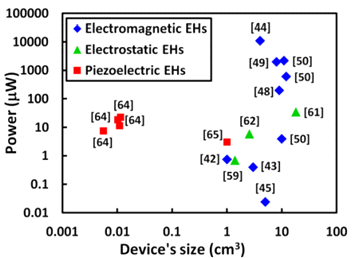
根据海旺等人[7]的观点,压电材料装置相较于电磁装置(EM)的主要优势在于:由于压电装置所存储的电荷密度高于电磁装置,因此具有更大的微型化潜力;不会产生电磁噪声,因而无需任何屏蔽措施;在30瓦以下的功率范围内具有更高的能量效率;并且由于压电材料不受端子处过载或短路的影响,电气故障更少。此外,汗[8]针对发电机在发电功率和设备尺寸方面进行了多项比较。就本案例而言,即对于低功耗应用(见图1),可以认为在小型设备中使用压电材料在发电能方面效率更高。

在将风能通过压电材料转换为电能的设备中,已有一些颇具前景的研究成果。多项研究提出了采用水平轴的风力发电机,利用梁使压电元件发生变形;压电元件本身即为梁,或被胶粘剂粘附于梁上 [9, 10, 11, 12]。通过连接至转子轴的凸起部件对梁施加直接作用力,从而实现压电材料的变形。
在Myers等人[13]和Chen等人[14]的实验中报道了类似实验,但此处设计的风力涡轮机通过一种特定机制将转子轴的旋转转换为线性运动,该机制负责使梁变形。
另一些研究也采用压电材料,将其制成梁或作为粘附在梁上的压电材料,用作变形元件 [15, 16, 17, 18, 19, 20, 21, 22]。然而,该系统的激励是由永磁体之间的磁相互作用引起的。其中一半磁铁被粘在中心(旋转)轴上,其余的则粘在梁上。吸引力和排斥力产生的磁力足以使梁发生变形,从而从系统中提取能量,且无需轴与梁之间发生接触。所有报道的发电机均为水平轴,除非所述风力发电机具有垂直轴[23, 24, 25]。Rezaei‐Hosseinabadi 等人[26]分析了这两种类型(水平轴/垂直轴),而 Wu 等人[27]描述了一种将轴的旋转运动转化为压电元件拉伸或压缩的机制。此外,该论文还利用了电磁能量产生方法。
与之前提到的装置相比,Viet 等人[28]和 Tao 等人[29]讨论的装置尺寸大于迄今为止所提出的其他风力涡轮机。此外,其运行机制也更为复杂,这削弱了此类装置的两个主要优势:微型化和高功率密度 (W/m³)。本文及其它若干研究中,功率密度定义为发电机每单位体积所产生的功率。McCloskey 等人 [30]提出了一种具有创新性的方案,即开发以树的形式存在的人工植物。当风吹过时,会弯曲覆盖有压电材料的叶片。尽管该研究颇具趣味性,但这种配置无法从所建议尺寸的装置中提取足够的能量。
Luong 和 Goo [15]提出了一种使用复合压电材料作为发电元件的小型风力涡轮机原型。在该装置中,发电机叶片朝向风向放置,提供扭矩以驱动转子旋转;磁铁被粘附在叶片表面,使压电梁(72 × 14 × 0.47 毫米³)发生变形,这些压电梁的自由端也粘有磁铁(重量为 9.36 克)。在此配置下,当磁铁间距为 6 毫米、风速为 2.7 米/秒时,获得了最大功率 2 毫瓦。在 100 千欧负载下产生的电压为 14 伏,振荡频率约为 15 赫兹。
基肖尔等人提出的设备[20]是为涉及低风速的应用而开发的。该原型(100×80×65毫米³)是一种直径为 72毫米的水平轴风力涡轮机,转子上分布有12个均等的永磁体。双晶型梁(60× 20× 0.7毫米³)在其末端粘有磁铁,并平行安装于转子轴。在这种情况下,在1.9米/秒的风速下,使用9千欧负载获得了0.45毫瓦的最大功率。
杨等人[21]提出了一种压电风力发电机(35 × 45 × 0.16毫米³),其组成包括一个螺旋体、一根带有 13克重量的永磁钕磁体的旋转轴。梁(38 × 78.5 × 0.2毫米³)由不锈钢制成,表面粘贴有压电材料,并在其自由端也粘有磁铁。单根梁的固有频率为10.25赫兹。该系统以650转/分(10.50赫兹)的旋转速度激发,相当于1.94米/秒的风速。因此,在磁铁间距为20毫米时,获得的最大电功率为3.14毫瓦。
基肖尔等人、杨等人以及Luong和Goo开发的该设备的功率密度[15],[20][21]分别为 4.221 μW/mm³, 0、536 μW/mm³ 和 3.701 μW/mm³。这些值是基于梁的尺寸、粘附在梁表面的压电材料以及获得的输出功率计算得出的。有关该主题的更多信息,读者可参考综述文章 [31, 32, 33, 34, 35, 36, 37]。这些文章不仅包含关于压电风车的研究,还涵盖了多种多样的应用。
因此,本文基于能量收集的概念,提出了一种采用压电换能器的风力涡轮机的设计及其数值与实验分析。通过模型和工作原型,评估了影响能量产生的不同参数。本工作的主要科学贡献是设计了一种小型机电装置,该装置易于组装,与文献中报道的其他装置相比,可为低功率应用提供较高的能量密度。
2. 原型设计与工作原理
该原型受风力发电机的启发,具有将风动能转化为电能的能力[38]。本研究中采用压电材料作为发电的活性元件。图2展示了所提出的装置及其主要部件。

该原型的整体尺寸约为84.5 × 87 × 20 mm³(不包括螺旋桨),螺旋桨直径为105毫米。该系统由三根钢梁简单嵌入组成,压电元件通过胶粘剂固定在梁的表面。在梁的自由端和轴上安装有钕铁硼永磁体,通过磁相互作用(在预先设定的频率下产生吸引力和排斥力)实现对梁的激励。此外,这些磁铁还用于质量调节,以改变梁的固有频率并局部增加梁的变形。
安装在轴上的磁铁尺寸为 5× 2.5× 2毫米³,质量为0.17克。该磁铁用胶粘剂固定在尺寸为 16 × 10 × 4毫米³的梁上。磁铁之间的间距为8毫米,在梁上产生0.03牛的磁力,引起变形但不会损坏压电材料。所用磁铁和梁的属性总结于表1中。
轴的旋转通过安装在轴上间距为 120°的磁铁转化为梁的变形。编码器用于测量轴的旋转。两根杆通过轴承支撑旋转轴,实现自由旋转。所有部件均固定在一个基座上,该基座为梁和杆提供支撑。基座、杆和编码器由ABS聚合物制成,采用3D打印工艺生产,而梁和旋转轴则由不锈钢制成。
本研究中探讨的关键原型参数包括:梁的几何形状对梁的变形和一阶共振频率的影响;在自由梁端添加质量及其对变形和频率的影响;粘接在梁表面的压电材料长度、压电材料类型,以及在考虑不同负载值(电阻)与压电材料串联时,其对电压和产生的电能的影响。
| Beam | 特性 | 符号 | 值 |
|---|---|---|---|
| 尺寸 | V | 60× 13× 0.15 毫米³ | |
| 弹性模量 | E | 200× 10⁹ Pa | |
| 密度 | ρB | 7850 kg/m³ | |
| Mass | mB | 0.918 克 |
| 磁铁1 | 特性 | 符号 | 值 |
|---|---|---|---|
| 尺寸 | V | 5× 2.5× 2毫米³ | |
| 密度 | ρI | 7500 千克/立方米³ | |
| Mass | mI | 0.17 克 | |
| 垂直牵引力 | – | 450 克 | |
| 磁性等级 | – | N44H | |
| 材料 | – | 钕铁硼 |
| 磁铁2 | 特性 | 符号 | 值 |
|---|---|---|---|
| 尺寸 | V | 16× 10× 4毫米³ | |
| 密度 | ρI | 7500 千克/米³ | |
| Mass | mI | 4.80 克 | |
| 垂直牵引力 | – | 3400 克 | |
| 磁性等级 | – | N35 | |
| 材料 | – | 钕铁硼 |
使用数值方法进行优化过程的主要原因是,从这一角度研究该问题的文献较少。优化能够更高效地利用时间,并大幅减少需要构建的原型数量。因此,仿真对于此类分析而言是不可或缺的工具。该方法论将在下一节中介绍。
3. 数值仿真
在进行实验测试之前,进行了数值仿真,以确定合适的梁几何结构、附加质量以及能够实现最高效率的压电体长度,即提供最大输出功率的配置。
根据参考文献[39],描述材料压电性能的本构方程基于以下假设:换能器中的总变形是机械应力引起的机械应变与施加电压差异导致的可控应变作用之和。在这些方程中,笛卡尔轴用数字而非字母表示,如图3所示;该图也是压电材料的示意图。
描述用作传感器的线性压电材料[40]机电行为的方程可写为如下形式:
$$
\varepsilon_i = S^D_{ij} \sigma_j + g_{mi} D_m \quad (1)
$$
$$
E_m = g_{mi}\sigma_i + \beta^\sigma_{ik} D_k \quad (2)
$$
指标 i, j = 1, 2, …, 6 和 m, k = 1, 2, 3 表示材料坐标系内的不同空间方向。σ 是机械应力矢量(N/m²),ε 是应变矢量(m/m),E 是施加的电场矢量(V/m),S 是柔度系数矩阵(m²/N),D 是电位移矢量(C/m²),g 是压电常数矩阵(m²/C),β 是介电常数分量(m/F)。

上标 D、E 和 σ 分别表示在恒定电位移、电场和机械应力条件下的测量值。
数值建模具有根本性的重要性,它决定了关键结构参数的影响,大大缩短了优化该设备所需的时间。
进行任何此类数值分析的第一步是建立控制该系统的运动方程。根据[41],哈密顿原理是实现这一目标最有效的方法之一。该原理也称为最小作用量[42],是有待采用的有限元法(FEM)的基础。针对通用压电梁[42]的能量收集任务,通过哈密顿原理可确定两个由耦合矩阵 Θ关联的结果方程。利用瑞利‐里兹近似法,我们可以写出:
$$
F(t)=(M_s+ M_p) \ddot{r}(t)+ C \dot{r}(t)+(K_s+ K_p) r(t)−Θv(t) \quad (3)
$$
$$
Θ^Tr(t)+ C_p v(T)= −q(t) \quad (4)
$$
方程(3)对应于结构域,方程(4)对应于压电域。此外,机械阻尼(C)的影响被包含在方程(3)中。Ms和Ks分别是结构元件的质量矩阵和刚度矩阵;Mp和Kp分别是压电元件的质量矩阵和刚度矩阵。Θ= ΘT是机电耦合矩阵;Cp是压电电容;F(t)是施加在梁上的外部激励力;r(t)是随时间变化的位移矢量,v(t)是作为时间函数产生的电压。
为了解决该问题,使用了名为 Ansys® Workbench 的商业软件,并结合专为此目的设计的应用程序定制工具包(ACT)PiezoAndMEMS®。同时还采用了用 ANSYS 参数化设计语言(APDL)编写的一些算法。
如上所述,所提出的发电机主要基于一组梁及其相应的压电材料,这将是仿真的重点。在此背景下,提出了一种梁结构,该结构在上下表面粘贴有两个压电换能器,并在其末端粘接有质量块,如图4所示。
外部激励由自由梁端的位移构成,该位移与由磁相互作用引起的实验激励估计值成正比。当压电材料发生变形时,其端子间会产生电势差(电压)。
采用SOLID226有限元模型来模拟压电材料,而对于梁及其末端的质量,则选用了SOLID186单元[43]。
为了模拟压电材料内部的电荷,使用了具有2个或3个节点自由度[43]的CIRCU94单元。这是通过 Workbench中ANSYS的APDL语言®实现的。
压电材料和梁均采用具有四边形单元的结构化网格。通过网格收敛性测试,梁/质量块的有限单元尺寸定义为1毫米,压电材料的有限单元尺寸定义为0.25毫米。另一个需要确定的重要参数是接触类型,以防止系统各部件之间的穿透。此处,接触类型已设置为绑定,接触的数学公式化通过多点约束 (MPC) 方法实现,并采用节点法向至目标类型的穿透检测。
进行了三种不同的分析:结构静力、模态和谐响应。最初选定了14个梁模型,从矩形几何形状开始,然后修改自由端形成三角形;图5显示了所有考虑的梁模型。梁的自由长度为50毫米,10毫米被压接,梁厚度保持恒定(0.15毫米)。
为了确定梁在自由端附加质量时的行为,不同质量的仿真从0.48 g到4.80 克的实验已进行。这些值显示在表2中。
最后,分析了梁上压电材料长度对系统参数的影响,采用了三种压电陶瓷长度:5 毫米、10 毫米和 15 毫米,如图6中蓝色部分所示。
用于分析的压电材料是由富士陶瓷公司制造的C‐64(软性)锆钛酸铅(PZT)压电陶瓷。其属性如表3所示。
试验中采用的平均全局阻尼因子 ξ为0.04或4%。初始连接到每个压电材料表面的电负载为20兆欧。该负载从20兆欧逐渐减小至1千欧,以模拟系统在开路和闭路状态下的行为。频率范围从0到50赫兹,每次试验的分辨率为1000个数据点。
| Mass | 最大质量的百分比 |
|---|---|
| 0.48 | 10 |
| 0.96 | 20 |
| 1.44 | 30 |
| 1.92 | 40 |
| 2.40 | 50 |
| 2.88 | 60 |
| 3.36 | 70 |
| 3.84 | 80 |
| 4.32 | 90 |
| 4.80 | 100 |


| C‐64(软) | 描述 | 符号 | 值 |
|---|---|---|---|
| 弹性模量 | Y1E= 1/S E | 59× 10⁹ Pa | |
| YE 3= 1/S E | 51× 10⁹ Pa | ||
| 密度 | ρ | 7700 kg/m³ | |
| 机电 | K31 | 0.35 | |
| 耦合因子 | K33 | 0.73 | |
| 介电 | ε11/ε0 | 1960 | |
| 常数 | ε33/ε0 | 1850 | |
| 压电材料 | d31 | −185× 10⁻¹² m/V | |
| 系数 | d33 | 435× 10⁻¹² m/V | |
| d15 | 670× 10⁻¹² m/V | ||
| 泊松系数 | νP | 0.34 | |
| 机械品质 | Qm | 84 | |
| 因子 | |||
| ## 4. 实验分析 | |||
| 根据之前的仿真结果,确定了梁模型和压电参数(特别是压电材料的长度),以获得性能最优的几何结构。 |
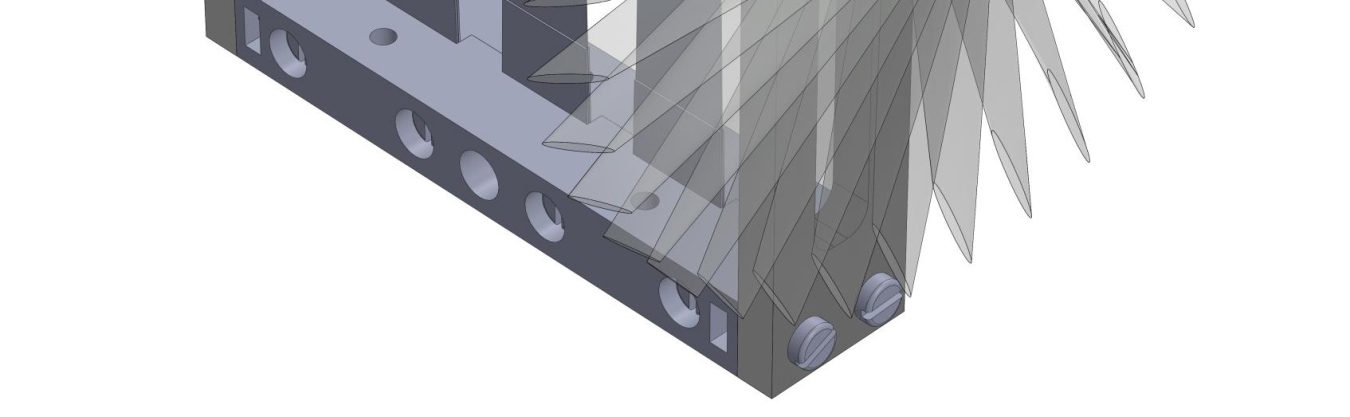
在实验测试中,粘接在梁端的质量块被替换为磁铁(磁铁2)。图7展示了所提出的原型及其主要部件。
与数值分析中一样,PZT C‐64型压电元件是负责发电的压电元件。首先确定了系统在开环和稳态条件下的动态系统行为;随后,向发电机施加扫频信号,激励频率在360秒内从7到32 Hz变化。在所有情况下,磁铁2被胶粘剂固定在梁上,而磁铁1被胶粘剂固定在轴上。轴上磁铁间距为8毫米。在仿真中,未考虑两个相邻梁之间的磁耦合。
采用皮带传动的直流电机驱动轴旋转,模拟风对螺旋桨的作用。由Arduino® Uno R3结合H L298N驱动桥控制直流电机。使用带有125C51型光耦的28孔盘式编码器测量轴旋转,信号由Arduino® Nano采集。
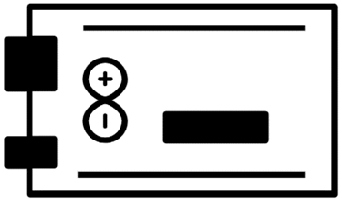
最后,Agilent Technologies®数字示波器(InfiniiVision DSO‐X 2014A)捕获生成信号。本实验的原理流程图和实验装置分别如图8和图9所示。
发电机在开路条件下的表征得到了频率与电压作为时间函数的关系。通过使用全波整流桥实现了闭路状态。



(使用1N60P 肖特基二极管和10 μF 聚酯电容)以获得直流电压;电路如图10所示。
通过这种方式确定了在压电材料的端子上添加负载(R)时其可产生的最大功率。该负载(R)通过 Minipa的电阻十进制箱MDR‐611型®施加。由于产生的电压(V)可使用示波器轻松获得,因此可以应用最大功率传输定理。当空载电压减半时,从发电机传递到负载的功率达到最大,这意味着所加负载等于发电机的内阻。


5. 结果与讨论
5.1. 数值结果
首次试验旨在确定悬臂梁沿其长度方向在梁表面的变形情况,试验时未附加质量且梁表面未进行压电粘接。为此,在梁的上表面沿其自由长度(50毫米)设置了多个变形区域,如图11所示。提取了当梁的自由端承受5毫米位移时的变形值。
图12 presents the deformation curves along lines created on the beams for all the considered models, without adding any mass to their free end.


从图12所示的曲线可以看出,三角形梁导致的平均变形较小;然而,这种变形在整个梁表面几乎均匀分布,使得可用于能量提取的区域更大。矩形梁虽然表现出更大的平均变形,但变形集中在压接处附近,因此适合能量提取的区域更小。图13分别显示了模型0、7和13在梁表面的变形分布。
此外,针对每个梁模型计算了一阶共振频率的值。数值结果如图14所示。可以看出,随着梁自由端宽度的增加,每个模型梁的一阶共振频率均有所降低,这可以通过质量的增加幅度大于结构刚度的增加幅度来解释,且该规律适用于所有采用的模型。
当在梁的自由端添加质量时,针对每个考虑的模型,沿梁长度方向的变形曲线如图15所示。在这些仿真中,添加到梁自由端的质量保持恒定(4.80 克)。
对比图12和图15,整体变形行为基本保持不变。然而,沿梁表面的平均变形水平显著增大。图16分别显示了考虑自由梁端质量贡献时模型0、7和13的梁表面的变形分布。
当附加4.80克的质量时,一阶共振频率发生显著变化;图17显示了所有考虑的不同模型的模拟共振频率。可以看出,对于恒定的质量值,系统的首阶固有频率没有显著变化,最大变化为0.5赫兹(3.7%),观察到的最小值和最大值分别为12.9赫兹和13.4赫兹。针对每个模型,评估了附加在自由端的质量对一阶共振频率的影响。图18提供了图形概览,数值数据列于表2中。
图18清楚地展示了附加质量增加时共振频率的下降;这种行为在所有模型中均相同。因此可以得出结论:自由梁端质量的增加会增大




结构的变形,从而导致系统共振频率降低。因此,附加质量可作为调谐工具使用。
压电材料的长度也对结构的响应有很大影响。一阶共振频率、峰值电输出电压和产生的电功率的值分别在图19、图20和图21中给出。考虑了所有模型,压电体长度变化(5、10 和 15 毫米),同时保持电负载(20 兆欧)、压电材料(C‐64)和梁端质量(4.80 克)恒定。
压电体长度对梁的一阶共振频率仅有中等程度的影响;这在一定程度上归因于压电元件引起的刚度变化。其长度越短,频率变化越低。
电压和功率的曲线图(图19和图20)表明,较大的压电材料并不一定能够产生更多的功率。实际上情况相反,较小的压电材料具有更高的效率。这是由于梁的变形主要集中在压接处附近,导致粘接的压电材料无法充分变形。此外,使用压电材料覆盖更大的面积也会增加材料失效的风险,因为这种陶瓷是一种脆性材料。


梁模型5和11在不显著改变系统共振频率的情况下表现出最佳响应。两者在略高于15赫兹的频率下,使用长度为5毫米的压电元件,均产生了约40 Vrms的电压和0.08毫瓦的功率。
当负载从 1 千欧 变化到 20 兆欧 时,模型 5、11 和 13 的系统行为变化如图22所示。添加模型13用于对比,因为其几何结构最简单。同样,在自由梁端添加了 4.80 克 的质量;压电元件长度为 5 毫米。
模型5和模型11在连接5兆欧电阻时提供了最高的电压,其值约为85.65Vrms。当连接1兆欧电阻时,梁模型11获得了最高功率,为5.58毫瓦。
鉴于这些结果,可以确定在考虑所提出的原型时,哪种模型最适合能量收集。对于建议的应用,模型11在以下参数下最为合适:压电材料长度为5毫米、PZT C‐64陶瓷材料,以及附加在梁末端的4.80克质量。
该配置在低频率下表现出最高的输出功率,这与其明显的承受能力相符。


施加的变形
5.2. 实验结果
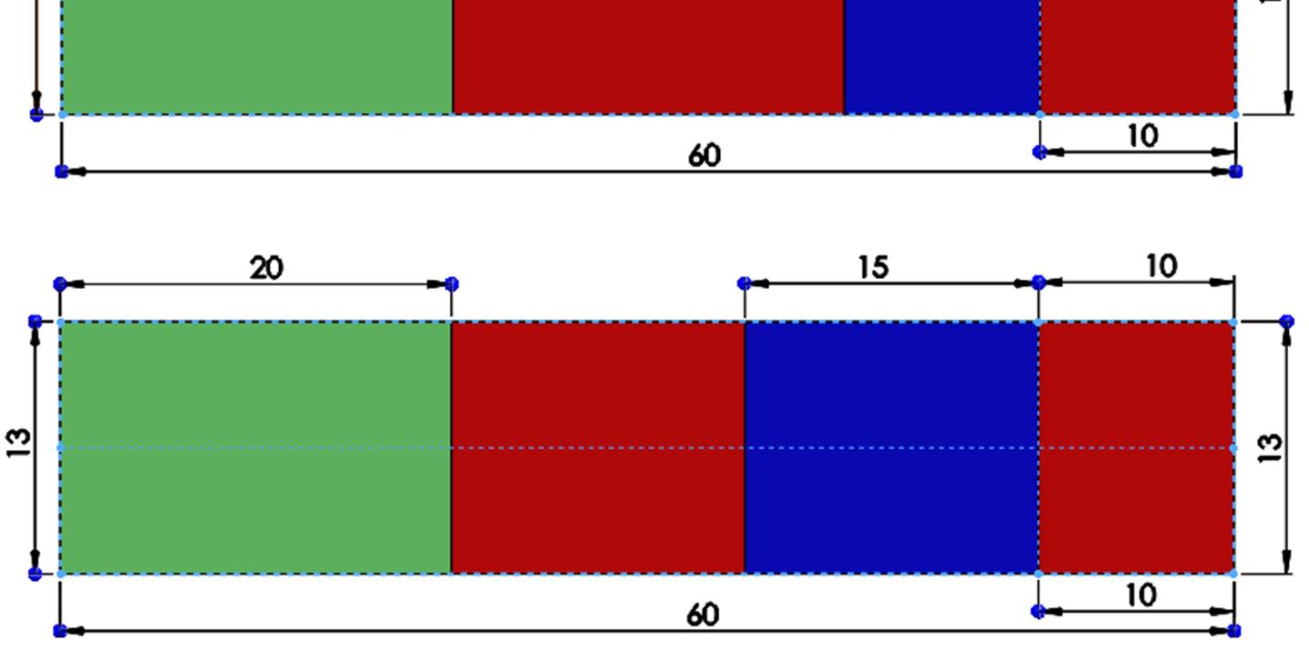
用于实验测试的模型是根据先前通过数值仿真获得的参数构建的。图23展示了所使用的结构、梁、压电材料和磁铁及其尺寸的示意图。
压电元件命名为压电元件1、2、3、4、5和6,被粘贴在三根钢梁的表面。此定义仅用于区分从同一陶瓷材料上切割出的各个矩形部分,并粘贴在梁的表面。第1和第2部分固定在第一根梁的上表面和下表面,即图7中右侧末端的梁。第3和第4部分位于中间的梁上,第5和第6部分位于左侧末端的梁上。在对系统施加约0.03 N磁力激励且频率为13.43 Hz的情况下测量生成电压,见图24。
图24显示,粘接在每根梁相对两侧的一对压电材料所产生的信号是同相的。这表明了良好的粘附性以及这些元件相对于极化方向的正确位置。需要注意的是,该振动频率是通过实验获得的平均频率;由于粘接、安装、螺钉紧固以及系统各部件之间相互作用存在微小变化,每根梁的共振频率略有不同。因此,确定了一个平均频率,使所有梁在其工作状态下均能获得可接受的性能。
每根梁上的两个压电材料并联连接;根据第一、第二和第三根梁分别命名为压电12、压电元件34和压电元件56。随后,所有压电元件并联连接(APP)。图25显示了获得的输出电压。
压电12产生的最高输出电压为72 Vpp,而压电元件34提供41 Vpp,压电元件56产生约30 Vpp。当三根梁并联连接(APP)时,获得的电压约为各个电压的平均值,即约43 Vpp。本实验中的激励频率为 13.43 Hz。选择并联连接旨在降低压电材料的阻抗,提高发电机的效率,并增加输出功率。
不同梁上压电元件的最大电压幅值差异可归因于粘接质量、梁在基座上的压接情况以及各梁共振频率之间的差异。由于这些原因,该结构的工作状态低于理想的发电条件。
对于确定为了确定系统的共振频率,进行了扫频信号激励。
频率是 s在360秒的时间间隔内从7到32 Hz扫频,对应增量为0.36 Hz
每5秒秒。该激励频率通过光电耦合器测量轴旋转来记录 er.
图26显示了激励信号随轴旋转频率的变化,以及磁铁之间相互作用施加的力随时间和磁铁间线性距离的变化。当使用前述扫频信号进行激励时,所有压电元件并联的响应如图27所示。
图28展示了系统在频域中的响应;这些数据是通过快速傅里叶变换技术获得的。图28的左侧显示了每个单独梁的第一振动模态的共振频率以及所有压电元件并联后的组合情况。压电元件12、34和56的共振频率分别为13.75赫兹、13.43 Hz和13.75赫兹。它们并联后的组合提供了13.84赫兹的共振频率。
在0.03牛顿的激励和13.43 Hz频率下,使用前述全波整流桥(见图9)时,所有压电材料并联配置下稳态中的直流电压值如图29所示。
在0到40秒之间观察到的初始上升段(图28)归因于连接在整流桥输出端的电容器的充电时间,其目的是确保信号的完全整流。压电元件12、34、56和APP在稳态下的平均电压分别为31.72伏特、16.35伏特、16.01伏特和17.53伏特。
扫频信号激励(在360秒内从7赫兹到32赫兹的扫频)这一特殊情况提供了随时间变化的输出电压,如图30所示。
在一阶共振频率下,压电元件12、34和56的峰值直流电压值分别为25.73 V、20.52 V和20.18 V。对于 APP配置,输出峰值电压为11.26 V。在第二共振频率下,产生的电压略高,压电元件12、34和56分别为 31.76 V、28.14 V和25.73 V。所有压电元件并联时,获得的电压为13.27 V。
通过最大功率传输方法,可以确定该装置的可用输出功率;将电阻负载连接到设备上,分别在有和没有整流桥的情况下进行测试。
从表4可以看出,未使用整流桥时压电材料获得的功率最高。输出功率在没有整流桥的情况下高得多,这可归因于整流电路的低效率。该电路不仅在二极管上产生电压降,还过度增加了系统的阻抗。根据表4,压电12和APP配置表现出最佳性能,产生的电功率分别为2.06 毫瓦和3.78 毫瓦。这些值对应于较低阻抗的电路(即没有整流桥)。
| 无整流桥 | |||||
| 电路 | 频率 | 电阻 | 电压 | 功率 | |
| 压电12 | 13.36 赫兹 | 580 千欧 | 34.6 伏峰峰值 | 2.06 毫瓦 | |
| 压电元件34 | 12.07 赫兹 | 720 千欧 | 20.1 伏峰峰值 | 0.56 毫瓦 | |
| 压电元件56 | 12.71 赫兹 | 730 千欧 | 23.3 伏峰峰值 | 0.74 毫瓦 | |
| APP | 13.71 赫兹 | 180 千欧姆 | 26.1 伏峰峰值 | 3.78 毫瓦 | |
| 带整流桥 | |||||
| 电路 | 频率 | 电阻 | 电压 | 功率 | |
| 压电12 | 13.36 赫兹 | 1220 千欧 | 13.5 伏峰峰值 | 0.59 毫瓦 | |
| 压电元件34 | 12.07 赫兹 | 1600 千欧姆 | 6.3 伏峰峰值 | 0.09 毫瓦 | |
| 压电元件56 | 12.71 赫兹 | 1730 千欧姆 | 6.6 伏峰峰值 | 0.11 毫瓦 | |
| APP | 13.71 赫兹 | 600 千欧 | 8.6 伏峰峰值 | 0.49 毫瓦 |
表5列出了压电12和应用程序在无整流桥情况下、针对不同有效体积的单位体积产生的电功率,即更常见的功率密度:仅压电材料的体积(案例1)、无压电元件的梁(案例2)、带压电元件的梁(案例3)、带压电元件的梁以及

| Case | 电路 | 功率 | 体积 | 功率密度 |
|---|---|---|---|---|
| 1 | 压电12 | 2.06 毫瓦 | 12.9 毫米³ | 159.7 微瓦/毫米³ |
| 1 | APP | 3.78 毫瓦 | 38.7 毫米³ | 97.7 微瓦/毫米³ |
| 2 | 压电12 | 2.06 毫瓦 | 109.5 毫米³ | 18.8 μW/mm³ |
| 2 | APP | 3.78 毫瓦 | 328.5 毫米³ | 11.5 μW/mm³ |
| 3 | 压电12 | 2.06 毫瓦 | 122.4 毫米³ | 16.8 μW/mm³ |
| 3 | APP | 3.78 毫瓦 | 367.2 毫米³ | 10.3 μW/mm³ |
| 4 | 压电12 | 2.06 毫瓦 | 762.4 毫米³ | 2.7 μW/mm³ |
| 4 | APP | 3.78 毫瓦 | 3287.2 毫米³ | 1.7 微瓦/毫米³ |
| 5 | 压电12 | 2.06 毫瓦 | 147030.0 毫米³ | 0.014 微瓦/毫米³ |
| 5 | APP | 3.78 毫瓦 | 147030.0 毫米³ | 0.025 μW/mm³ |
磁体(情况4)。最后包含了发电机所占的体积(情况5)。
图31显示了本研究获得的能量密度与前述研究之间的关系比较。表5中列出的值已根据各自采用的体积与其他作者的数据进行了适当比较。可以确定,本研究所获得的功率密度与

文献中报道的值,甚至高于大多数研究设备的值。由于案例2最常被用作计算设备功率密度的参考,因此压电12的输出功率为18.8 μW/mm³,应用程序的输出功率为11.5 μW/mm³最具代表性。
6. 结论
本文对一种新型发电机进行了全面的表征,考虑了影响能量产生的主要因子以及系统在负载下的行为。
根据数值分析可以得出,将模型11与5毫米长的压电材料和粘接在自由梁端的4.80克质量块组合是发电的最佳配置。实际实验证实了这一预期。在考虑APP配置且电路无整流桥的情况下,获得的最佳输出功率为3.87毫瓦。在所评估的研究中,本工作开发的原型具有最高的功率密度,对于压电12(单根梁的体积)为18.8 μW/mm³,对于APP(三根梁的体积)为11.5 μW/mm³。
尽管测得的输出功率可能较小,但足以用于为多个物联网设备供电、为电池充电或为低功耗的自主电路提供能量。通过增加梁的数量可以提高该设备的输出功率,但这会带来发电机体积和质量增加的负面影响。
未来的工作应重点关注材料疲劳,这意味着要分析压电材料的使用寿命与轴的旋转次数之间的关系。
尝试通过风对螺旋桨的作用来激活系统,并验证能量发电情况。此外,还需分析胶粘剂对数值与实验响应的影响。




















 4286
4286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








