机器学习笔记1-回归分析-线性回归-相关分析-最小二乘

1回归分析:

定义:利用样本(已知数据),产生拟合方程,从而对位置数据进行预测

 

用途:预测,判别合理性

 

例子:利用身高预测体重,利用广告费用预测商品销售量;

 

线性(一定是一次的)回归分析:一元线性,多元线性;广义线性

函数关系:是确定性关系,但是线性拟合是相关关系,这是有本质区别的.

 

非线性回归分析:

 

困难:选定变量(多元的);避免多重选定;观察拟合方程,避免过度拟合,检验模型是否合理.

 

1.1关系:

函数关系:确定性的关系

相关关系:非确定性的关系

1.2 相关系数:

r(-1 1)正负关系不代表拟合程度,只代表增加或者减少,比如相关系数是正的,则x增加,y增加.

r越贴近1,则拟合的越好,但是永远不会是1;

 

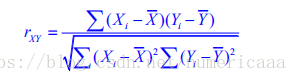
1.3 参数:

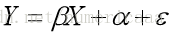
斜率 截距 误差项 这就是需要拟合出来的回归方程

关键是怎么求出来,问题来了,其实如果我有很多样本的话,那么拟合出来的方程可以有很多,就是说 B a 的值可以有很多,但是我要如何确定哪个B a是最好的呢?

给你样本如何确定出最好的回归方程?

(1) RSS:平方误差和

  

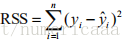
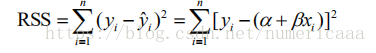
给我样本,只要让RSS最小就行了,从而可以求出来B a

 

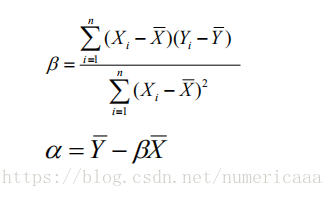
得到了这个其实没什么用,因为需要X拔和Y拔,这是总体均值,但是我没有总体的,只能用样本估计总体的.

 

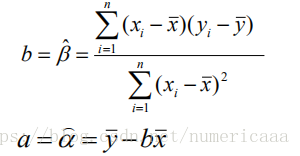
得到解决