算法题目中图和树的存储及遍历

原创已于 2024-03-24 15:13:05 修改 · 321 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#单链表

于 2024-02-23 23:58:27 首次发布

文章介绍了邻接表在图和树数据结构中的应用，包括如何通过h[],e[],ne[]数组存储和连接节点，以及深度优先遍历(DFS)和宽度优先遍历(BFS)的实现方法，重点展示了如何添加节点和进行遍历操作。

邻接表的方式存储图和树

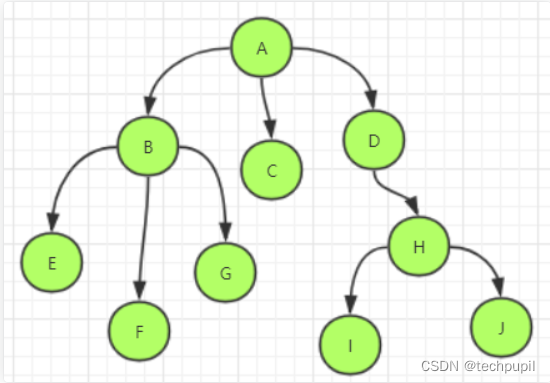
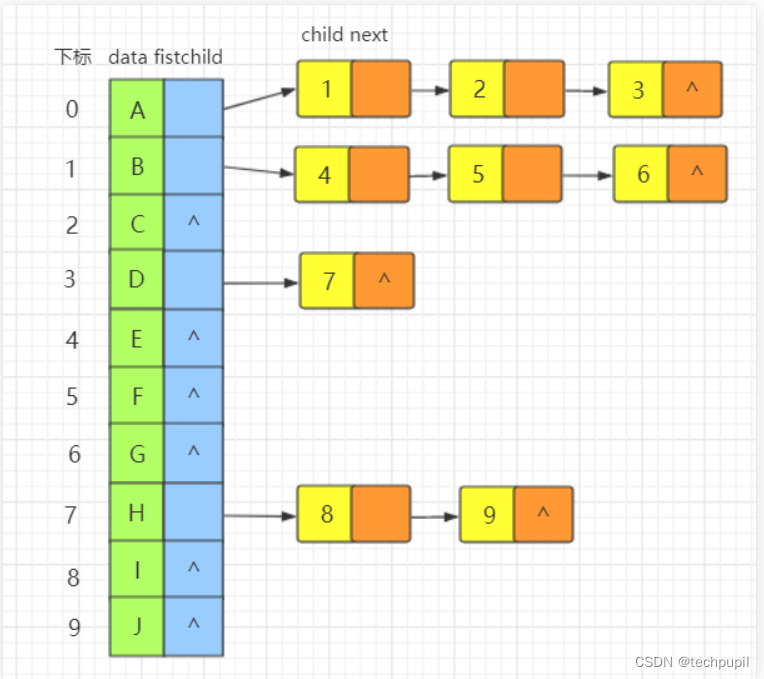
在这里插入图片描述

这就是邻接表，就是将每个结点的孩子结点用链表表示出来，再将所有结点以数组形式连起来。

存储树和图我们需要三个数组，h[N], e[N], ne[N],分别表示邻接表，结点值，结点的next值，h[i]是以i为父节点的最后一个插入的结点的地址，e[i]是i结点的序号，next[i]是i的下一个结点的地址。还需要一个变量idx，表示当前需要插入的结点。

例如我们现在有一个需求是将2号结点插入到1号结点下面，变成它的孩子结点。
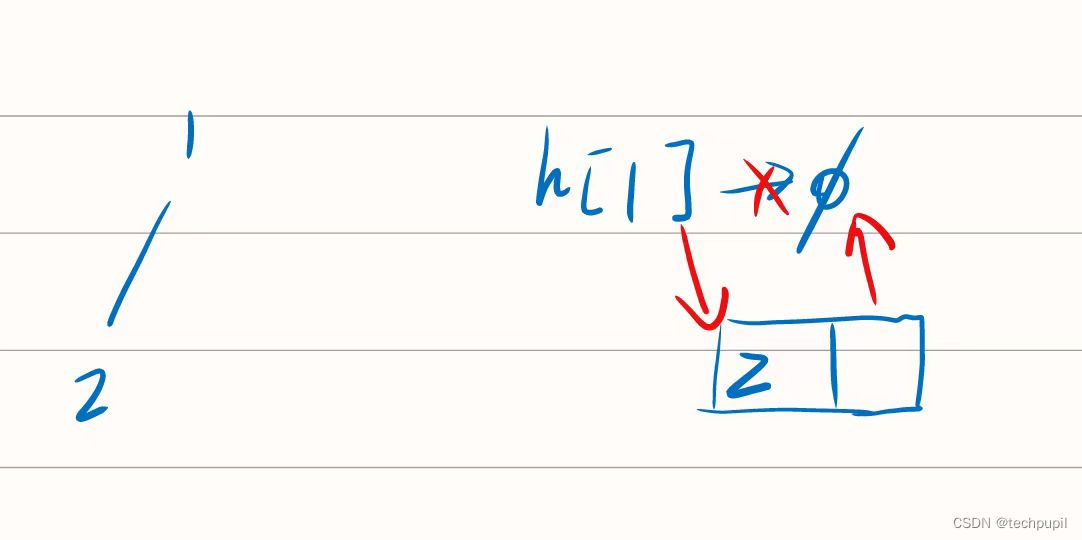
请添加图片描述
这就是我们的思路，h数组初始值都为-1，因为没有插入结点（-1就代表空）。
先让2号结点的next值为-1，然后h[1]指向2号结点，这样他们三个就连成一串了。
抽象的用代码实现一下

a->b
void add(int a, int b){
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx;
	idx ++;
}

这个函数就可以为我们实现添加一条边。

文章参考：https://www.cnblogs.com/linfangnan/p/12745834.html

树和图的遍历

深度优先遍历

void dfs(int u) {
    st[u] = true;// 标记一点，这个点已经被搜过了

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];// j是取出第i个点的序号
        if (!st[j]) dfs(j);
    }
}

宽度优先遍历
求最短路径问题

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int bfs(int u) {
    int hh = 0, tt = 0;
    q[0] = 1; // 第一个元素入队
    
    memset(h, -1, sizeof h);

    d[1] = 0;
    while (hh <= tt) {
        int t = q[hh++];

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (d[j] == -1) {  // 没有被更新过
                d[j] = d[t] + 1;
                q[++tt] = j; // 邻点入队
            }
        }
    }
}