CF - Star MST(组合数学 2200)

思路

• 考察与1结点相连的边构成的生成树。要使得最小生成树权值总和等于这颗生成树的权值总和，当且仅当该生成树的所有叶节点两两间的边权值都大于等于从1结点指向这两个叶节点的边权值
• 于是当1号结点指向这些叶节点的权值确定时，方案数也就确定了。最终变成一个组合数学问题

DP

• 当1结点与其余结点相连的权值确定后，可确定此情况下的一种方案数
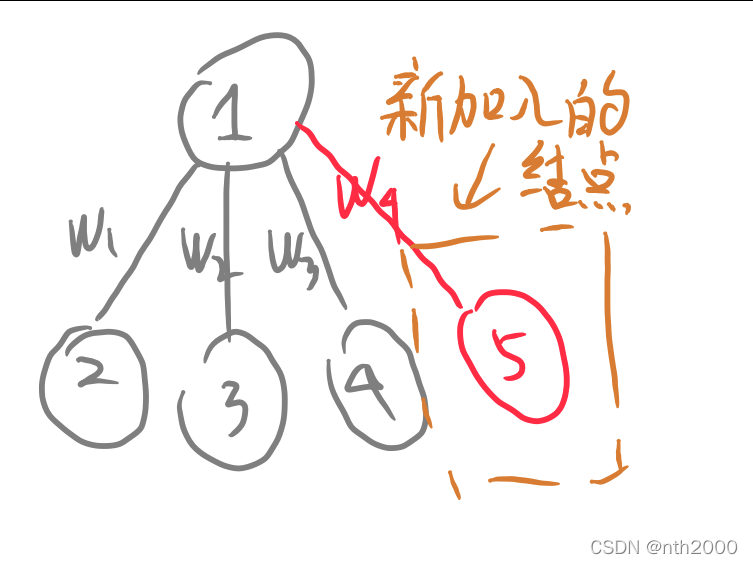
• 当一个新结点加入时，方案数量会增加多少？、
  • 由于该结点大小与已有结点与1相连的边的权值是不确定的，因此方案增加数量是不确定的
• 如果将1结点与其余结点相连的权值按非递减顺序排序。固定一种非递减方案（可以很容易求解其余连接)连接的方案数量，设为num），由其可以生成方案的数量为
  $$\frac{(n-1)!}{i_1!i_2!\cdots i_o!}\cdot num$$
  其中$i_1,i_2\cdots i_k$是从小到大的元素相同的个数。

例如对非递减方案$[1,1,1,3,3,4,5,6,6]$，其可生成的方案数量为$\frac{8!}{3!2!1!1!2!}\cdot num$

• 针对于所有非递减方案求总和，就可求出最终结果。

设$DP[i][j]$：处理到第i个结点，非递减序列末尾最大值为j，每个dp[i][j]都共有一个$(n-1)!$的因子。除了i=n-1的情况，其余的只是为了方便计算，实际意义并不明确。

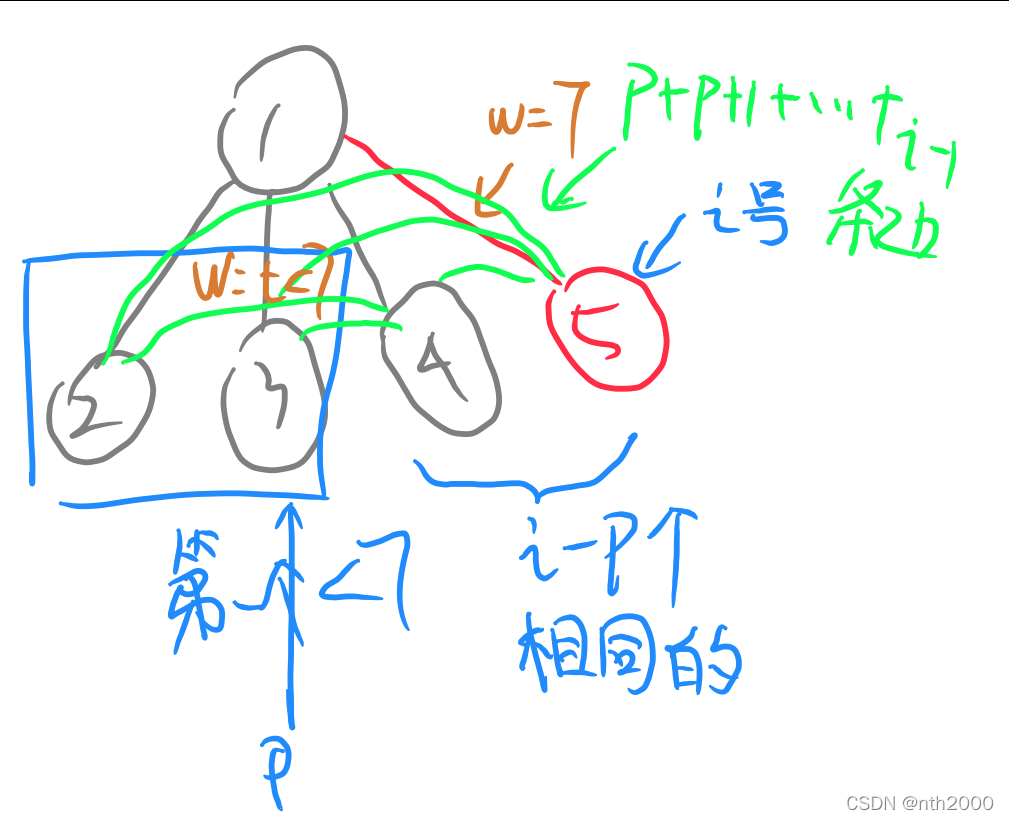
• 向前找第一个小于j的权值对应的结点设置为p，则j对应的边一共有$i-p$个。从这个标号p的结点的后一个结点开始，每个结点都能与自身前面的所有结点连接，即共有$p+p+1+\cdots i-1$条边，每条边的权值取值都能够从[j,k]中任意取，即每条边都有k-j+1种可能性。于是
  $$DP[i][j]=\sum _{t<j}\sum _{p<i}\frac{DP[p][t](k-j+1{)}^{p+p+1+\cdots i-1}}{(i-p)!}$$
  可以令$DP[0][0]=(n-1)!$，这样后继所有状态都有该因子了。
• 实际上这里的DP本质上还是计算了所有非递减排列的可能性，再对每种方案的可能性求和。可以注意提取公因子(i-p)!加以理解。
  

代码

#include <bits/stdc++.h>
using namespace std;

#include<iostream>
#include<vector>
#include<string>
#include<set>
#include<algorithm>
#include<map>
#include<queue>
#include <chrono>
#include<math.h>
#include<unordered_map>
using namespace std;
const int N = 1e5+5;
const int S =  500;
const long long mod = 998244353;
typedef long long ll;

ll quickpow_mod(ll a,ll b)  //带模快速幂
{
    ll ret = 1;
    a %= mod;
    while(b > 0)
    {
        if(b & 1) ret =  (ret * a) % mod;
        b = b >> 1;
        a = (a * a) % mod;
    }
    return ret;
}

ll calc_inv(ll a)
{
    return quickpow_mod(a,mod-2);
}


int main()
{
    long long n,k;
    cin >> n>>k;
    ll dp[n][k+1];
    ll fa[n+1];fa[0]=1;  
    for(int i =1;i<n+1;i++) fa[i] = (fa[i-1] * i) % mod;
    for(int i = 0;i<n;i++)
    {
        for(int j = 0;j<k+1;j++)
         dp[i][j] = 0;
    }
    dp[0][0] = fa[n-1];
    //求阶乘逆元
    for(int i=0;i<n+1;i++) fa[i] = calc_inv(fa[i]);
    //处理幂次信息
    ll pow_d[k+1][n*n];
    for(int i = 0;i<=k;i++)
    {
        for(int j = 0;j<n*n;j++)
         {
             pow_d[i][j] = quickpow_mod(i,j);
         }
    }
    for(int  i = 1;i<=n-1;i++)
    {
        for(int j = 1;j<=k;j++)
        {
            for(int p = 0;p<i;p++)
            {
                for(int q = 0;q<j;q++)
                {    dp[i][j] += (dp[p][q] * pow_d[k-j+1][(i-1+p) * (i-p) / 2])%mod * fa[i-p];
                    dp[i][j] %= mod;
                }
            }
            
        }
    }
    ll ans = 0;
    for(int i  =1;i<=k;i++) 
    {ans = ( ans + dp[n-1][i] ) % mod;}
    cout << ans << endl; 
    system("pause");
    return 0;
}