高数笔记一函数与极限

1、极限运算法则

【定理一】有限个无穷小之和仍是无穷小。

【定理二】有界函数与无穷小的乘积仍是无穷小。

【推论一】常数与无穷小的乘积是无穷小。

【推论二】有限个无穷小的乘积是无穷小。

【定理三】（极限运算的分配律）
若
$$limf(x)=A$$

$$limg(x)=B$$

则
$$1im[f(x)+g(x)])$$
存在，则
$$lim[f(x)+g(x)]=A+B=limf(x)\pm limg(x)$$
【定理四】

若
$$limf(x)=A$$

$$limg(x)=B$$

且
$$1im[f(x)\ast g(x)])$$
存在，则
$$lim[f(x)\ast g(x)]=A\ast B=limf(x)\ast limg(x)$$
【定理五】

若
$$limf(x)=A$$

$$limg(x)=B$$

B≠0，且
$$1im\frac{f(x)}{g(x)}$$
存在，则

$$1im\frac{f(x)}{g(x)}=\frac{A}{B}=\frac{limf(x)}{limg(x)}$$
对商的极限运算法则， 应注意条件:

(1)、极限 lim f(x)=A，lim g(x)=B均存在。

(2)、作分母的函数g(x)的极限 lim g(x)=B≠0。

当这两个条件中有一个不满足时， 不可使用商的极限运算法则。 这一点在初学时很容易被忽视。

2、两个重要极限

2.1、重要极限一

2.2、重要极限之二

3、无穷小的比较

4、函数的连续性与间断点

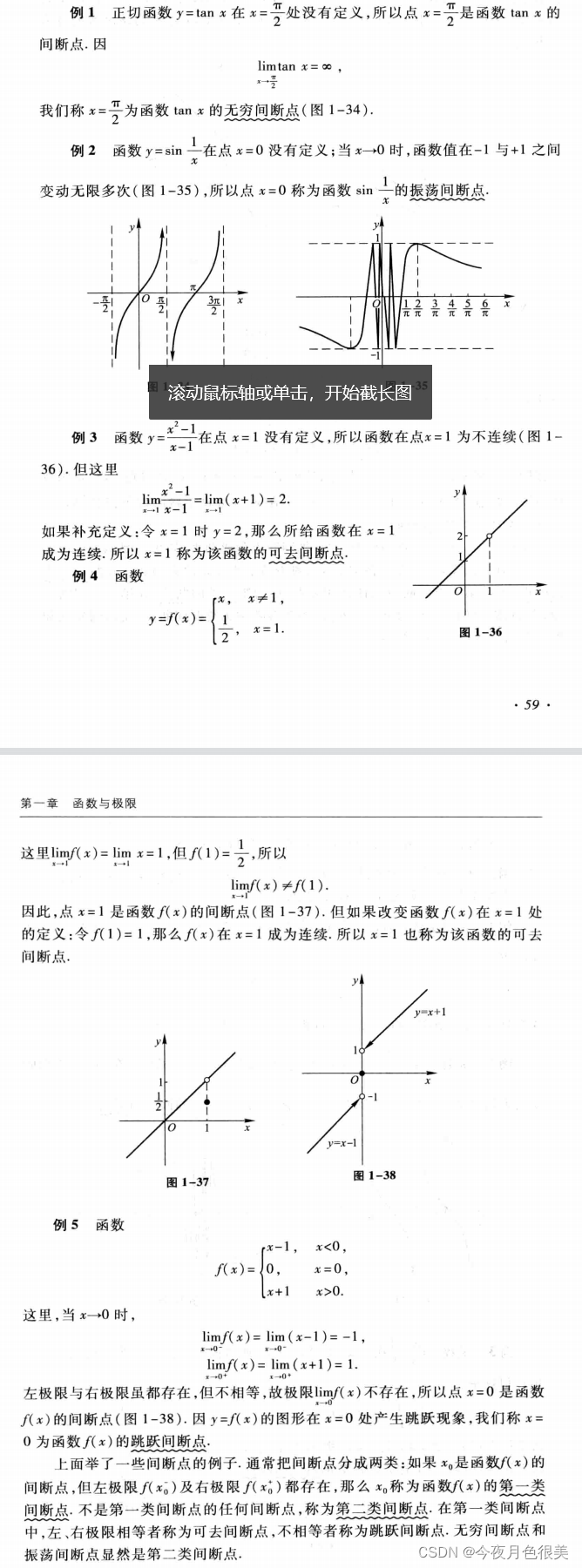
5、备注

连续的几何含义是一笔画，可导的几何含义是光滑