绿色全要素生产率GTFP的计算方法梳理

原创 已于 2024-12-16 17:44:41 修改 · 3.1k 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#学习 #学习方法 #笔记 #机器学习 #人工智能

于 2024-12-13 10:44:56 首次发布

1 由来

在投入产出的关系中，越来越多的学者发现产出不仅仅只有期望产出，还有非期望产出，例如当在有GDP产出时候，在工业领域必然会产生二氧化碳、废水等非期望产出。那么原本CCR（规模报酬不变,即投入产出同比例增加）、BCC模型（规模报酬可变)考虑的投入越少导致产出越多就不能说明一个DMU是有效率的，如何将非期望产出考虑进去就成了问题。因此在此之后发展出SBM、DDF模型。

2. DDF模型（方向距离函数模型）

3.SBM模型

Tone 于2001年提出SBM模型（Slack Based Measure),优点在于成功解决了经向模型在效率评价中对于松弛变量的忽视问题。

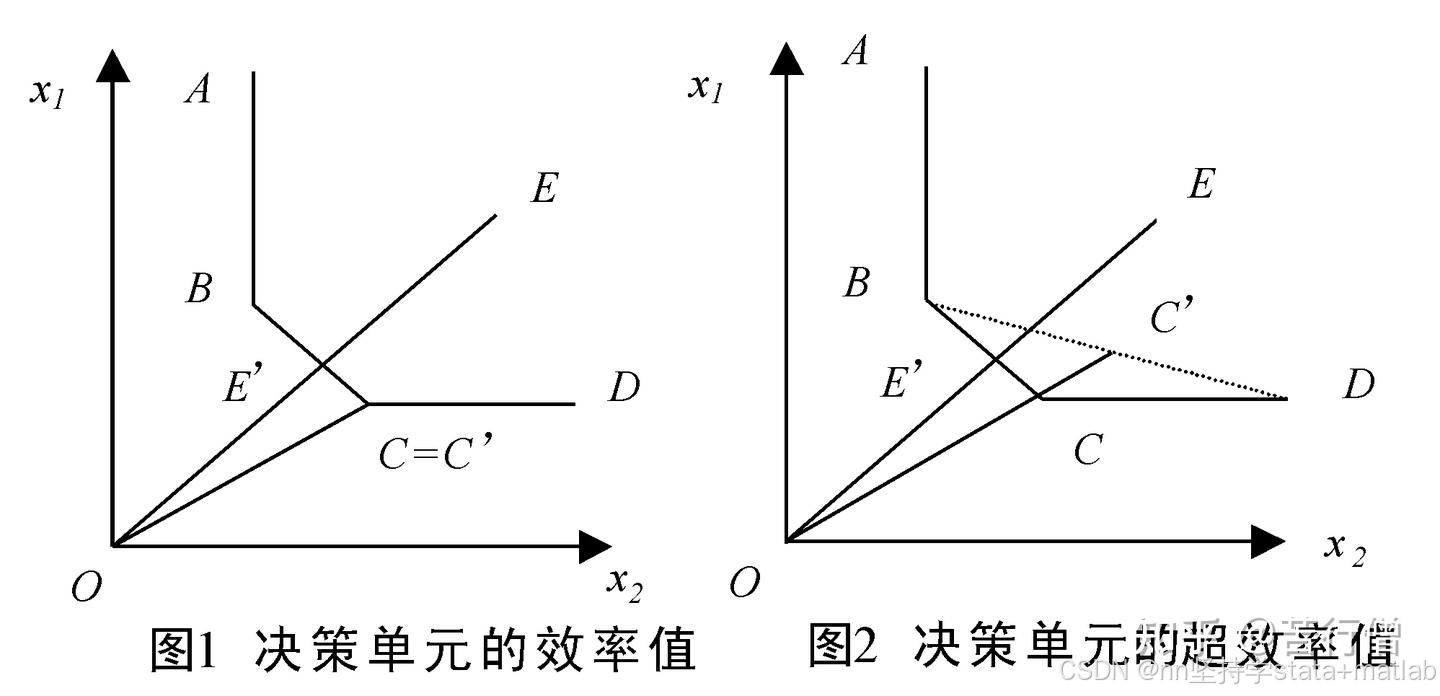
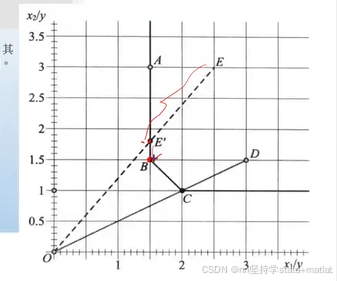
横轴：单位产出的投入1；

纵轴：单位产出的投入2；

投入越少越好，即前沿面越靠近原点对应的效率越高

GG‘：表示无效的程度

OG'：表示有效的程度

1-GG'/OG'：表示有效程度的衡量换句话说，就是径向效率值\theta = \frac{OG'}{OG}

小贴士：径向改进VS松弛改进

径向改进：投入同比例减少，例如EE'；

松弛改进：投入不同比例减少，例如E'B

投入角度在衡量效率的时候没有考虑生产的松弛假定生产已经到前沿面了，那么投入要减少多少才能到标杆
产出角度在衡量效率的时候没有考虑投入的松弛假定投入已经到前沿面了，那么产出要增加多少才能到前沿面
非角度同时考虑投入和产出即考虑了投入减少的部分，也考虑了产出增加的部分

4.EBM模型（混合距离函数）

5.Malmquist指数、ML指数

补充请看：一文详细说明SBM、SBM-DDF、DDF、NDDF、ML指数是什么（学习笔记）_sbm-ddf模型-优快云博客

6.计算方法

分类方法优缺点
参数法随机前沿分析法（SFA）需要准确预测生产函数的特定形状，然后利用SFA计算出生产过程的效率值
非参数法数据包络分析法（DEA）DEA-SBM超效率模型包含非期望产出无需提前设定投入和产出 直接按的生产函数关系
Global-Malmquist-Luenberger（GML）指数对数据量纲没有要求，信息反映充分，规避线性无解的问题

GML指数：前为止有三种方法可以实现。

第一种是早期用的比较多的基于Kaoru Tone（2001）的SBM模型（SBM-GML），

第二种是Fukuyama&Weber（2009）提出的方向SBM距离函数模型(GML-DDF)。

最后一种方法是Rolf Fare&Grosskopf（2010）基于方向距离函数的SBM模型（SBM-DDF模型），

三种方法的优劣及合理性评价，目前暂无定论。

GM（Global Malmquist）指数是通过全局DEA模型计算的M指数
ML（Malmquist_Luenberger）指数考虑非期望产出DEA模型计算的M指数
GML（Global Malmquist_Luenberger）指数考虑非期望产出的全局DEA模型计算的M指数
M指数FGNZ分解
RD分解
Zofio分解

参考文献：

贸易综合竞争力对绿色全要素生产率的影响研究——王双  西南财经大学硕士论文

https://zhuanlan.zhihu.com/p/495166671

SBM模型原理详解_哔哩哔哩_bilibili

地级市绿色全要素生产率(2000-2019).xlsx
01-16
2000-2019年 421个行政区样本，四个直辖市为区级层面数据，其他行政区为地市层面样本，在数据包络分析框架下，利用SBM模型和Malmquist生产率指数对城市全要素生产率增长进行测度，该数据通过大量计算得到。
绿色全要素生产率测算代码（SBM模型、超效率SBM模型代码案例数据）
samLi0620的博客
12-16 3442
SBM是Slacks-Based Measure 或Slack Based Measure的缩写，一般翻译为基于松弛值测算的模型，与DEA两用，即SBM-DEA。Tone(2001)构建了一个新的 DEA 模型即 SBM（Slacks-Based Measure）模型，是一个非径向（non-radial）非角度（non-oriented）DEA 模型。“径向的”要求在评价效率时投入或产出同比例变动，而“角度的”要求在评价效率时做出基于投入（假设产出不变）或者基于产出（假设投入不变）的模型选择。
2005-2021年 中国各省绿色全要素生产率GTFP原始数据+测算结果
2401_84585615的博客
06-30 1616
定义：GTFP指标在传统的全要素生产率的基础上，加入了对环境成本和资源利用效率的考量。目的：评估经济增长过程中的生产率水平，同时考虑对环境的影响。
matlab的绿色全要素生产率非期望DEA-ML算法.docx
05-07
matlab的绿色全要素生产率非期望DEA-ML算法.docx
绿色全要素生产率测算（SBM模型代码+案例+数据）
ky路上的博客
04-13 2369
本思想，它用“最小的”或“匹配最紧密的”凸面球壳包络投入产出数据集，所得到数据集。“又快又好”发展的经济学内涵。经济和社会发展各方面，切实保护和合理利用各种资源，提高资源利用率，以尽可能少的资。源消耗，获得最大的经济效益和社会效益，实现人与自然和谐发展、经济社会可持续发展。“快”即经济增长速度高，“好”则是污染少、能耗低，“又快又好”即以较少的资源投入。edMeasure的缩写，一般翻译为基于松弛值测算的模型，与DEA两用，即SB。件、相关讲解文件以及示例数据，数据用了最简单的yxx1等展示，代码做了详。
各省GTFP绿色全要素生产率面板数据（计算方法在文件）2004-2018年
03-01
各省GTFP绿色全要素生产率面板数据 1、数据来源：自主计算整理 2、时间跨度：2004-2018年 3、区域范围：全国30个省和直辖市 4、数据说明： 部分数据如下： 计算方式附在网盘中
2000-2021年上市公司/企业绿色全要素生产率stata（含原始数据及stata代码）
zxwk01的博客
04-16 2301
另，文章代码含稳健性检验用替换指标，使用SBM-SML方法。能源投入：以上市公司所在城市工业企业用电量作为代理指标。本文采用SBM-GML模型，对企业绿色全要素生产率进。：以企业的主营业务收入作为期望产出的代理指标。已通过实证验证显著性，可放心使用，如有需要，劳动投入：以企业的员工人数作为代理指标。采用永续盘存法估算每个企业的资本投入。非期望产出：企业所在地级市的三废。测算企业绿色全要素生产率。可提供答疑/修改等服务。
GML指数和ML指数测算gtfp_GML和ML指数_GTFP测算代码_DEA的GML分解_GML指数
09-10
DEA非期望产出和GML和ML的matlab代码，其中Malmquist-Luenberger（ML）Global-Malmquist-Luenberger(GML)。
地级市绿色全要素生产率GTFP，四种GML指数EBM-GML、SBM-GML SBM-DDF原始数据+测算结果
07-01
283个地级市绿色全要素生产率GTFP年度数据(2006-2019)，采用了四种GML指数测算方法，分别是EBM-GML、SBM-GML 、GML-DDF 、SBM-DDF。并且均分解为了EC、TC。 说明：此数据均为本人整理并测算，是本人论文写作用到的...
2004-2018年全国各省绿色全要素生产率gtfp面板数据
05-07
2004-2018年全国各省绿色全要素生产率gtfp面板数据 1、时间：2004-2018年 2、来源：各省nj、能源nj、环境nj 3、指标： 年份、地区、就业人员（万人）（劳动投入）、固定资本存量（亿元）、能源消费量（万吨标准煤）...
2004-2018年全国各省绿色全要素生产率GTFP面板数据(原始数据和测算结果)
09-06
2004-2018年全国各省绿色全要素生产率gtfp面板数据
matlab测算绿色全要素生产率GTFP
04-17
关于使用SBM模型计算生产率指数（M, ML, GM, GML, L指数等），我 们目前为止发现有三种方法可以实现。第一种是早期用的比较多的基于Kaoru Ton e (2001)的SBM模型（2002.1），第二种是Fukuyama & We ber (2009)提出的...
各省GTFP绿色全要素生产率面板数据（2004-2018年）
li514006030的博客
04-22 5263
1、数据来源：中国环境统计年鉴 2、时间跨度：2004-2018年 3、区域范围：全国30个省和直辖市 4、数据说明： 部分数据如下： 5、计算方式： 以2004年为基期，基于非期望产出，使用非导向的SBM模型-GML指数进行测度，超效率和非超效率的，一样算了一份，结果与MAXDEA软件测算的一样。 2004年的GTFP均为1，MI指数即绿色全要素生产率的变化率，不过绿色全要素生产率我也折算出来了。 其中：投入1为劳动投入，采用各省份年末就业人员数，数据来源于各省市自治区的统计..
绿色全要素生产率
X200416的博客
01-07 2511
经济学全要素生产率
上市公司绿色全要素生产率（GTFP）数据（2007-2022年）
paperdata666的博客
12-14 745
企业绿色全要素生产率的投入和产出指标的测度如下：1、要素投入：劳动投入以企业员工数作为代理变量；2、期望产出：以企业营业收入作为企业期望产出的代理变量。3、非期望产出：以企业从业人员占所在城市城镇人员就业比重对“工业三废”即工业二氧化硫、工业废水、工业烟粉尘排放量进行换算，作为企业非期望产出的代理变量。数据来源：《中国城市统计年鉴》、《中国环境统计年鉴》、上市公司年报、上市公司社会责任报告。指标：证券代码、年份、企业绿色全要素生产率、绿色技术效率变化指数、绿色技术进步变化指数。
SBM模型、超效率SBM模型代码（原始面板数据、MATLAB）
2401_84585615的博客
07-18 3781
SBM模型和超效率SBM模型是评估决策单元效率的有力工具。通过这些模型的Matlab实现，用户可以方便地在自己的研究和实践中应用这些先进的效率评价方法。数据名称：SBM模型、超效率SBM模型代码请注意，这些模型的实现需要一定的Matlab编程知识，以确保正确应用和解释结果。通过这些工具，用户可以深入分析DMUs的效率，并采取相应的优化措施。SBM模型、超效率SBM模型代码（原始面板数据、MATLAB）
运用SBM-GML方法测算绿色全要素生产率（2021）
weixin_45892228的博客
05-11 2011
运用SBM-GML方法测算绿色全要素生产率（2021）运用SBM-GML方法测算。运用SBM-GML方法测算绿色全要素生产率（2021）运用SBM-GML方。运用SBM-GML方法测算绿色全要素生产率（2021）运用SBM-运用SBM-GML方法测算绿色全要素生产率（202。运用SBM-GML方法测算绿色全要素生产率（GML方法测算绿色全要素生产率（2021）运用SBM-GML方法测算绿色全要素。法测算绿色全要素生产率（2021）绿色全要素生产率（2021）
windows上位机开发学习（二）计时器案例（下） int大小
最新发布
qq_43091070的博客
11-29 693
本文介绍了Windows上位机开发中计时器案例的代码实现过程。首先通过工具箱添加Timer控件并设置1秒间隔，然后详细讲解了核心代码：1)声明全局变量记录时间；2)实现"开始"按钮点击事件，解析用户输入并初始化计时器；3)编写Timer的Tick事件处理逻辑，每秒更新界面并判断倒计时结束。文章还展示了完成效果图，并附带单片机int类型大小对照表。最后提供了C#串口通信编程的学习参考网址，欢迎交流讨论。
DEA-CCR模型
05-05
<think>好的，我现在需要回答用户关于DEA-CCR模型的问题，包括计算方法、代码实现以及相关原理。首先，我需要回顾一下DEA和CCR模型的基本概念。数据包络分析（DEA）是一种用于评估决策单元（DMU）效率的非参数方法，而CCR模型是其中基于规模报酬不变假设的模型。 用户提到了数据包络分析法（DEA）的R实现和Python实现，所以需要结合这些引用中的信息。引用1、2、3中提到了CCR和BCC模型的区别，CCR模型是规模报酬不变，而BCC是可变。用户主要关注CCR，所以需要集中讨论这一点。 接下来，用户想知道计算方法。根据引用3，CCR模型是径向的，允许输入或输出按相同比例调整。数学推导方面，可能需要写出线性规划的形式。例如，对于每个DMU，最大化效率值θ，满足输入和输出的约束条件。这里需要确保使用正确的数学公式，并用LaTeX格式呈现。 代码实现方面，用户可能希望看到Python或R的示例。引用1提到了R实现，引用2是Python，所以需要提供两种语言的代码片段。例如，Python中使用PuLP库来构建线性规划问题，R中使用lpSolve包。需要检查这些包是否适用于CCR模型，并写出正确的模型设置。 另外，用户可能对步骤感兴趣，比如数据准备、模型构建、求解和结果分析。需要分步骤解释，确保结构清晰。同时，要注意将数学公式和代码分开，符合用户要求的独立公式用$$...$$，行内用$...$。 还要生成相关问题，可能涉及模型假设、优化方法、与其他模型的比较等。需要根据引用中的信息，比如提到BCC、SBM模型，所以可以生成相关问题。 需要确保回答正确，比如CCR模型的线性规划形式是否正确，代码是否能够运行（可能需要简化，但逻辑正确）。同时，引用文献末尾添加引用标识，例如引用1、2、3中的内容，并在适当的地方标注。 现在，我需要组织这些内容，先解释CCR模型的原理，数学公式，然后分步骤说明计算方法，接着提供Python和R的代码示例，最后生成相关问题。确保符合用户的格式要求，使用中文，LaTeX正确，结构清晰。</think>### DEA-CCR模型详解 #### 一、模型原理 CCR模型基于**规模报酬不变**假设，通过线性规划方法评估决策单元（DMU）的相对效率[^3]。其核心思想是：在保持产出不变时，寻找输入的最小缩减比例$\theta$；或在输入不变时，寻找产出的最大扩展比例$\phi$。 #### 二、数学公式（投入导向型） 对第$k$个DMU的效率计算可表示为： $$ \begin{aligned} \text{max} \quad & \theta \\ \text{s.t.} \quad & \sum_{j=1}^{n} \lambda_j x_{ij} \leq \theta x_{ik}, \quad i=1,...,m \\ & \sum_{j=1}^{n} \lambda_j y_{rj} \geq y_{rk}, \quad r=1,...,s \\ & \lambda_j \geq 0, \quad \theta \text{ 无限制} \end{aligned} $$ 其中： - $x_{ij}$为第$j$个DMU的第$i$项输入 - $y_{rj}$为第$j$个DMU的第$r$项输出 - $\lambda_j$为权重变量 - $\theta$表示效率值（$\theta=1$时DMU有效） #### 三、计算步骤 1. **数据标准化**：确保输入输出指标同向性 2. **构建线性规划模型**：为每个DMU建立单独模型 3. **求解效率值**：通过单纯形法等求解器计算 4. **有效性判断**：θ=1且松弛变量为0时DMU有效 #### 四、代码实现 ##### Python实现（使用PuLP库） ```python from pulp import * def dea_ccr(inputs, outputs): n_dmu = len(inputs) efficiency = [] for k in range(n_dmu): prob = LpProblem("DEA_CCR", LpMaximize) theta = LpVariable("theta") lambdas = [LpVariable(f"lambda_{j}") for j in range(n_dmu)] # 目标函数 prob += theta # 约束条件 for i in range(len(inputs[0])): prob += lpSum(lambdas[j] * inputs[j][i] for j in range(n_dmu)) <= theta * inputs[k][i] for r in range(len(outputs[0])): prob += lpSum(lambdas[j] * outputs[j][r] for j in range(n_dmu)) >= outputs[k][r] prob += lpSum(lambdas) == 1 # 规模报酬可变时去掉此约束 status = prob.solve() efficiency.append(value(theta)) return efficiency ``` ##### R实现（使用lpSolve包） ```r library(lpSolve) dea_ccr <- function(inputs, outputs) { n_dmu <- nrow(inputs) efficiency <- numeric(n_dmu) for (k in 1:n_dmu) { f.obj <- c(1, rep(0, n_dmu)) # 目标函数θ f.con <- matrix(0, nrow = ncol(inputs) + ncol(outputs) + 1, ncol = 1 + n_dmu) # 输入约束 for (i in 1:ncol(inputs)) { f.con[i, ] <- c(-inputs[k,i], inputs[,i]) } # 输出约束 for (r in 1:ncol(outputs)) { f.con[ncol(inputs)+r, ] <- c(0, outputs[,r]) } # 凸性约束 f.con[ncol(inputs)+ncol(outputs)+1, ] <- c(0, rep(1, n_dmu)) f.dir <- c(rep("<=", ncol(inputs)), rep(">=", ncol(outputs)), "==") f.rhs <- c(rep(0, ncol(inputs)), outputs[k,], 1) result <- lp("max", f.obj, f.con, f.dir, f.rhs) efficiency[k] <- result$objval } return(efficiency) } ``` #### 五、应用实例 假设3个DMU的输入输出数据： | DMU | 输入1 | 输入2 | 输出1 | |-----|-------|-------|-------| | A | 2 | 3 | 5 | | B | 3 | 4 | 7 | | C | 4 | 5 | 9 | 运行代码后将输出各DMU的θ值，θ=1的DMU为有效单元。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值