【神经网络框架】非局部神经网络

一、非局部操作的数学定义与理论框架

1.1 非局部操作的通用公式

非局部操作（Non-local Operation）是该研究的核心创新点，其数学定义源自经典计算机视觉中的非局部均值算法（Non-local Means）。在深度神经网络中，非局部操作被形式化为：

其中：

1.2 与传统操作的对比分析

（1）与卷积操作的对比
传统卷积操作仅处理局部邻域（如3×3或5×5窗口），依赖深层堆叠逐步扩大感受野。而非局部操作直接计算全局位置间的依赖关系，具有以下优势：

• 单层即可捕获长程依赖
• 避免信息传递的路径损耗
• 支持跨时空维度的交互

（2）与循环操作的对比
RNN/LSTM等循环结构通过时间步迭代处理序列，存在梯度消失/爆炸问题。非局部操作：

• 并行计算所有位置关系
• 突破时间步限制
• 适用于空间和时空场景

（3）与全连接层的对比
全连接层的权重固定且与输入无关，而非局部操作：

• 动态计算位置间关系
• 保持输入输出位置对应
• 支持可变尺寸输入

1.3 归一化因子设计

归一化因子 C(x) 的选择影响模型稳定性：

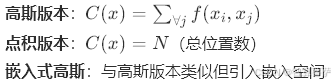
二、非局部操作的具体实现形式

2.1 相似性函数f的四种设计

论文系统性地探索了四种成对函数设计：

（1）高斯函数（Gaussian）

• 直接计算原始特征的余弦相似度
• 保持经典非局部均值的数学形式
• 计算复杂度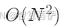：（N为位置数）

（2）嵌入式高斯（Embedded Gaussian）

其中 

• 引入可学习的线性变换（1×1卷积）
• 将相似度计算映射到嵌入空间
• 与自注意力机制等价（Softmax归一化）

（3）点积（Dot Product）

• 去除Softmax激活
• 归一化因子设为位置总数N
• 实验显示与高斯版本效果相当

（4）拼接（Concatenation）

• 借鉴关系网络（Relation Networks）设计
• 引入非线性激活函数
• 需学习参数向量

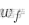
2.2 特征变换函数g的设计

统一采用线性变换：

• 通过1×1卷积实现
• 减少通道数以降低计算量（典型为原通道数1/2）
• 保持位置对应关系不变

2.3 实例化对比实验结论

通过Kinetics数据集上的消融实验发现：

• 不同f函数版本性能差异小于1%（72.7%~72.9%）
• 自注意力（嵌入式高斯）并非性能提升的关键因素
• 非局部性（全局交互）本身才是核心优势

三、非局部块的结构设计

3.1 残差连接形式

将非局部操作封装为可插入模块：

3.2 模块结构示意图解析

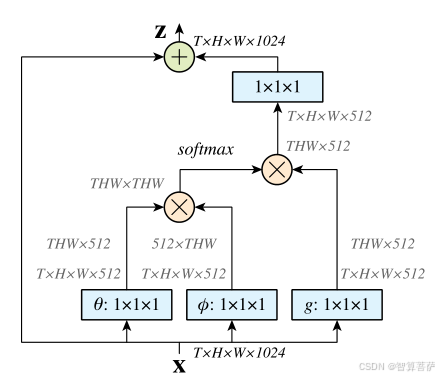
非局部块包含以下组件：

1. θ路径：1×1卷积降维（通道数减半）
2. φ路径：1×1卷积降维（同θ路径）
3. g路径：1×1卷积降维
4. 相似度计算：矩阵乘法实现成对关系
5. Softmax归一化（仅高斯版本）
6. 特征聚合：矩阵乘法结合g路径特征
7. 1×1卷积升维：恢复原始通道数
8. 残差相加：保留原始特征信息

3.3 模块插入策略

实验发现最佳实践：

• 插入位置：ResNet的res3和res4阶段
• 插入密度：每两个残差块插入一个非局部块
• 深层插入效果下降（因空间分辨率过低）

四、高效实现策略

4.1 通道缩减技术

• θ、φ、g路径均采用通道减半设计
• 计算量降低约50%
• 与ResNet瓶颈设计思想一致

4.2 空间下采样技巧

4.3 计算复杂度分析

以典型视频特征图尺寸为例：

• 输入尺寸：T×H×W = 4×14×14
• 原始计算量：784×784矩阵乘法
• 下采样后：196×196矩阵乘法
• FLOPs减少约75%，内存占用显著降低

五、与3D卷积的对比分析

5.1 计算效率对比

（基于ResNet-101基准）

模型类型	参数量倍数	FLOPs倍数	精度（Top-1）
C2D基线	1.0×	1.0×	73.1%
I3D_3×3×3	1.5×	1.8×	74.1%
NL C2D（5块）	1.2×	1.2×	75.1%

5.2 特性对比

特性	3D卷积	非局部操作
感受野类型	局部窗口	全局交互
时空关系建模	显式时空滤波	隐式相似度计算
参数依赖性	静态卷积核	动态依赖关系
长程依赖捕获能力	需深层堆叠	单层即可实现
计算复杂度	与核尺寸立方成正比	与位置数平方成正比