梯度下降法是机器学习和神经网络学科中我们最早接触的算法之一。但是对于初学者,我们对于这个算法是如何迭代运行的从而达到目的有些迷惑。在这里给出我对这个算法的几何理解,有不对的地方请批评指正!
梯度下降法定义
(维基百科)梯度下降法,基于这样的观察:如果实值函数  在点
在点  处可微且有定义,那么函数
处可微且有定义,那么函数  在
在  点沿着梯度相反的方向
点沿着梯度相反的方向  下降最快。
下降最快。
因而,如果
对于  为一个够小数值时成立,那么
为一个够小数值时成立,那么 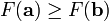 。
。
考虑到这一点,我们可以从函数  的局部极小值的初始估计
的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列 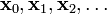 使得
使得
因此可得到
如果顺利的话序列 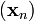 收敛到期望的极值。注意每次迭代步长
收敛到期望的极值。注意每次迭代步长  可以改变。
可以改变。
下面图片示例了这一过程,这里假设  定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数
定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数  为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数
为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数  值最小的点。
值最小的点。
梯度下降法几何解释:
由于我们的任务是求得经验损失函数的最小值,所以上图的过程实际上是一个“下坡”的过程。在每一个点上,我们希望往下走一步(假设一步为固定值0.5米),使得下降的高度最大,那么我们就要选择坡度变化率最大的方向往下走,这个方向就是经验损失函数在这一点梯度的反方向。每走一步,我们都要重新计算函数在当前点的梯度,然后选择梯度的反方向作为走下去的方向。随着每一步迭代,梯度不断地减小,到最后减小为零。这就是为什么叫“梯度下降法”。
那么,为什么梯度的方向刚好是我们下坡的反方向呢?为什么我们不是沿着梯度的方向下坡呢?这是因为,只有沿着梯度的反方向,我们才能下坡,否则就是上坡了……举个例子,在y=f(x)的二维平面上,规定好x轴和y轴的方向后,如果曲线f(x)的值是随着x的增加上升的,那么它在某一点的切线的数值一定是正的。反之,若曲线f(x)的值是随着x的增加下降的,则它在下降的某一点的切线的数值一定是负数。梯度是方向导数在某一点的最大值,所以其值必然是正数。如果沿着梯度方向走,经验损失函数的值是增加的……所以,我们要下坡,就必须沿着梯度方向的反方向了。
梯度上升法几何解释:
相对于梯度下降法,还有梯度上升法。(注意减号变成加号了)
其基本原理与下降法一致,区别在于:梯度上升法是求函数的局部最大值。因此,对比梯度下降法,其几何意义和很好理解,那就是:算法的迭代过程是一个“上坡”的过程,每一步选择坡度变化率最大的方向往上走,这个方向就是函数在这一点梯度方向(注意不是反方向了)。最后随着迭代的进行,梯度还是不断减小,最后趋近与零。
有一点我是这样认为的:所谓的梯度“上升”和“下降”,一方面指的是你要计算的结果是函数的极大值还是极小值。计算极小值,就用梯度下降,计算极大值,就是梯度上升;另一方面,运用上升法的时候参数是不断增加的,下降法是参数是不断减小的。但是,在这个过程中,“梯度”本身都是下降的。
注:这里的梯度减小指的是梯度的数值大小,不包含方向的正负号。








 本文深入解析梯度下降法和梯度上升法的几何概念,通过直观的图片和数学表达,阐述了这两种算法如何在优化问题中找到极小值和极大值。重点解释了梯度方向与下坡、上坡的关系,以及如何通过调整步长和迭代过程实现收敛。此外,还介绍了梯度下降法与梯度上升法在实际应用场景中的不同用途。
本文深入解析梯度下降法和梯度上升法的几何概念,通过直观的图片和数学表达,阐述了这两种算法如何在优化问题中找到极小值和极大值。重点解释了梯度方向与下坡、上坡的关系,以及如何通过调整步长和迭代过程实现收敛。此外,还介绍了梯度下降法与梯度上升法在实际应用场景中的不同用途。
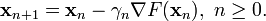
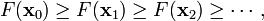


















 1534
1534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








